本文简单实现了浙江大学陈灏硕士学位论文《光学稀疏孔径成像系统图像恢复算法研究》(2017)中4.2章节提及的改进维纳滤波算法。
前情提要:维纳滤波函数中不同K(噪声与原属图像功率谱之比)的取值对应复原效果不同,当K值比较小时(10^-4~10^-3)时,图像边缘存在着严重的振铃效应,而随着K的慢慢增大,振铃效应越来越弱直至消失,最后图像变得越来越模糊。所以作者提出了一中基于PSNR的图像质量评价体系的改进的维纳滤波算法,目的是选取最优的K值,使得用该K做维纳滤波得到的复原后的图像与原始图像最为接近(PSNR值最大)。
原文在正文第36页:




但原文似乎没有对此方法的详细介绍,所以姑且用一个简单的方法考虑:每次K按一定方式,从10^-5~到10^3量级增加,判断以当前K值进行维纳滤波得到的复原图像与原始图像的差异度(即PSNR)是否比历史最优值更好,类似于遍历找最大值的策略,但量级跳度过大,如果按照 10^-5~到10^3量级的原则来的话,需要进行10^8次计算,这无疑增加了计算量。根据观察,可以根据原文中K值与PSNR值曲线来进行K的跳度限制:最开始随着K值的增加,PSNR迅速增大到最大值后开始越来越平稳地减小,相对应可设置最开始阶段K值的增加(步长)为10^-5级,之后根据K值来对步长进行扩增,如10倍等。当然精度可以根据需求或者个人喜好等随意修改,在代码中,初始化K为0,步长step为1*10^-5(matlab中可以简单表示为1e-5),当K值增加到是步长的100倍时,步长相应地增加到原来的10倍,直至K大于1000,停止循环。
matlab中,可直接使用函数deconvwnr进行维纳滤波操作。为方便起见,将同系函数的使用方法进行总结:
| 调用方式 | 方法名 | 参数解释 |
| J = deconvwnr(I,psf) J = deconvwnr(I,psf,nsr) J = deconvwnr(I,psf,ncorr,icorr) | 维纳滤波 | psf:点扩展函数(卷积核) nsr:加性噪声的噪信比(K) ncorr:噪声自相关函数 icorr:I的自相关函数 |
|
| Lucy-Richardson滤波 | iter:迭代次数 dampar:阻尼阈值 weight:权重矩阵 readout:读出相机噪声 subsample:子采样倍数 |
|
| 盲去卷积 | psfi:点扩展函数的初始估计 psfr:复原后的点扩展函数 fun:描述点扩展函数附加约束的函数句柄 |
|
| 最小二乘滤波 | np:加性噪声强度 lrange:搜索最优解范围 regop:正则算子 lagra:拉格朗日乘子 |
psf相当于卷积核,由文件读取,也可以通过其他方式设置。psnr可以直接调用matlab函数,亦可以手动实现。data为n*4维矩阵,每一行存储了每次计算对应的次数、K值、步长和PSNR值。
代码和注释如下,相应条件可自行调整:
clc
clear
close all
f=rgb2gray(imread('timg.jpg'));
[m,n]=size(f);
Psf=load('psfdata.txt');
% C=uint8(conv2(f,Psf,'same')); %另一种卷积方式
C = imfilter(f,Psf,'conv','circular'); %卷积得到模糊图像
K=0;
step=1e-5; %步长
Img=[];%最大PSNR对应的图像
best_PNSR=-Inf;%最大值
best_K=-Inf;%最大值对应的K
t=1;%计算次数
while K<=1000img=deconvwnr(C,Psf,K);%维纳滤波new_PSNR=psnr(img,f);%计算滤波复原后的图像与原图的PSNR值data(t,1:4)=[t,K,step,new_PSNR];%储存次数、K值、步长、PSNR值if new_PSNR>best_PNSR%最大PSNR对应的更新best_PNSR=new_PSNR;best_K=K;Img=img;endif K/step>100%步长的更新step=step*10;endK=K+step;%K值的更新t=t+1;
end
%对K值和PSNR值进行绘制,由于图像前后差距过大,只取前120行
x=data(1:120,2);
y=data(1:120,4);
plot(x,y)
xlabel('K值')
ylabel('PSNR')
figure,
subplot(131),imshow(f),title('原始图像')
subplot(132),imshow(C),title('模糊图像')
subplot(133),imshow(Img),title('复原图像')执行结果如下:
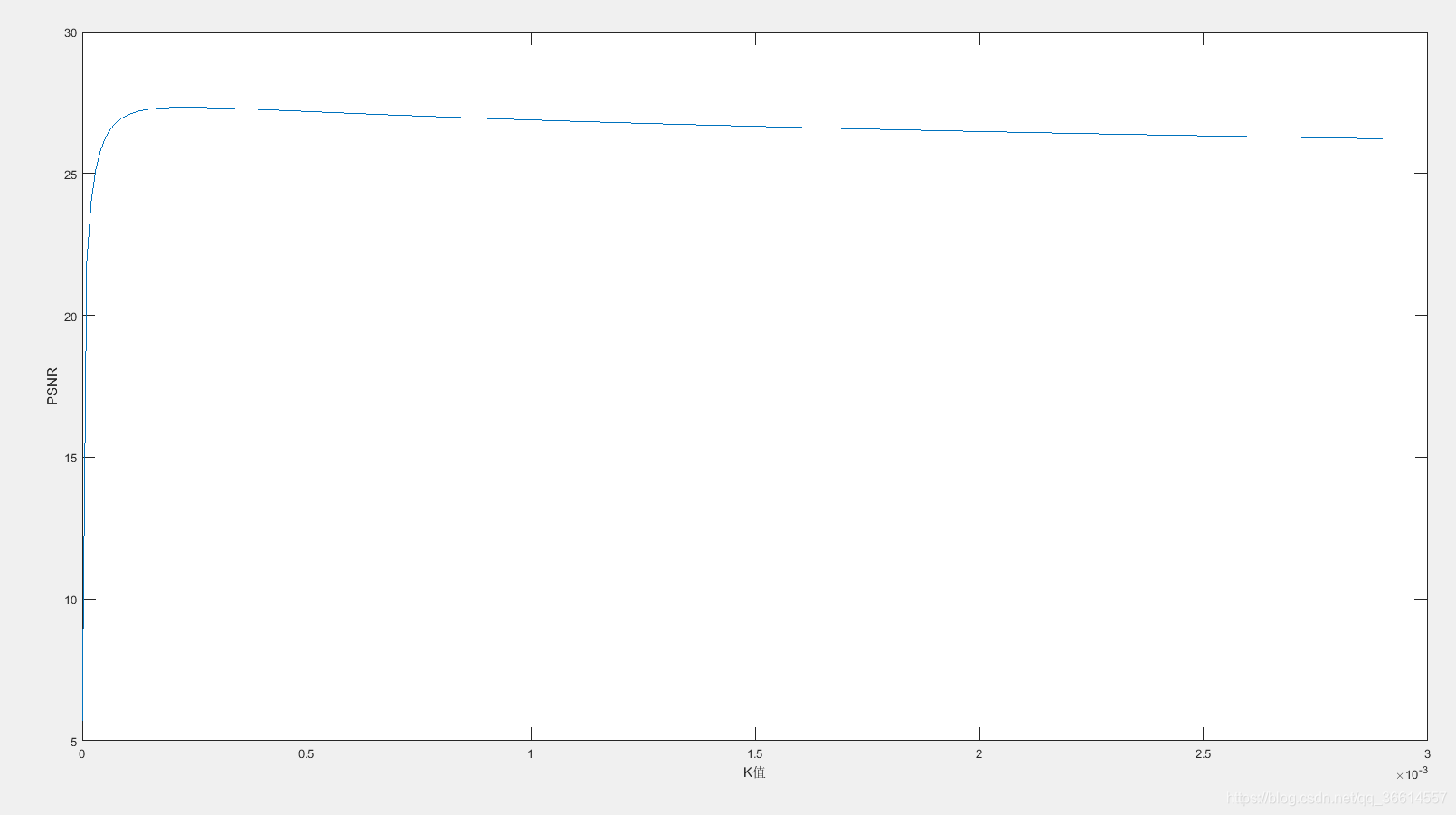

模糊图像PSNR: 19.9984
复原图像PSNR: 27.3320
psf文件见https://github.com/typeisgod/CSDN