三其他BC

1.Repeated BC

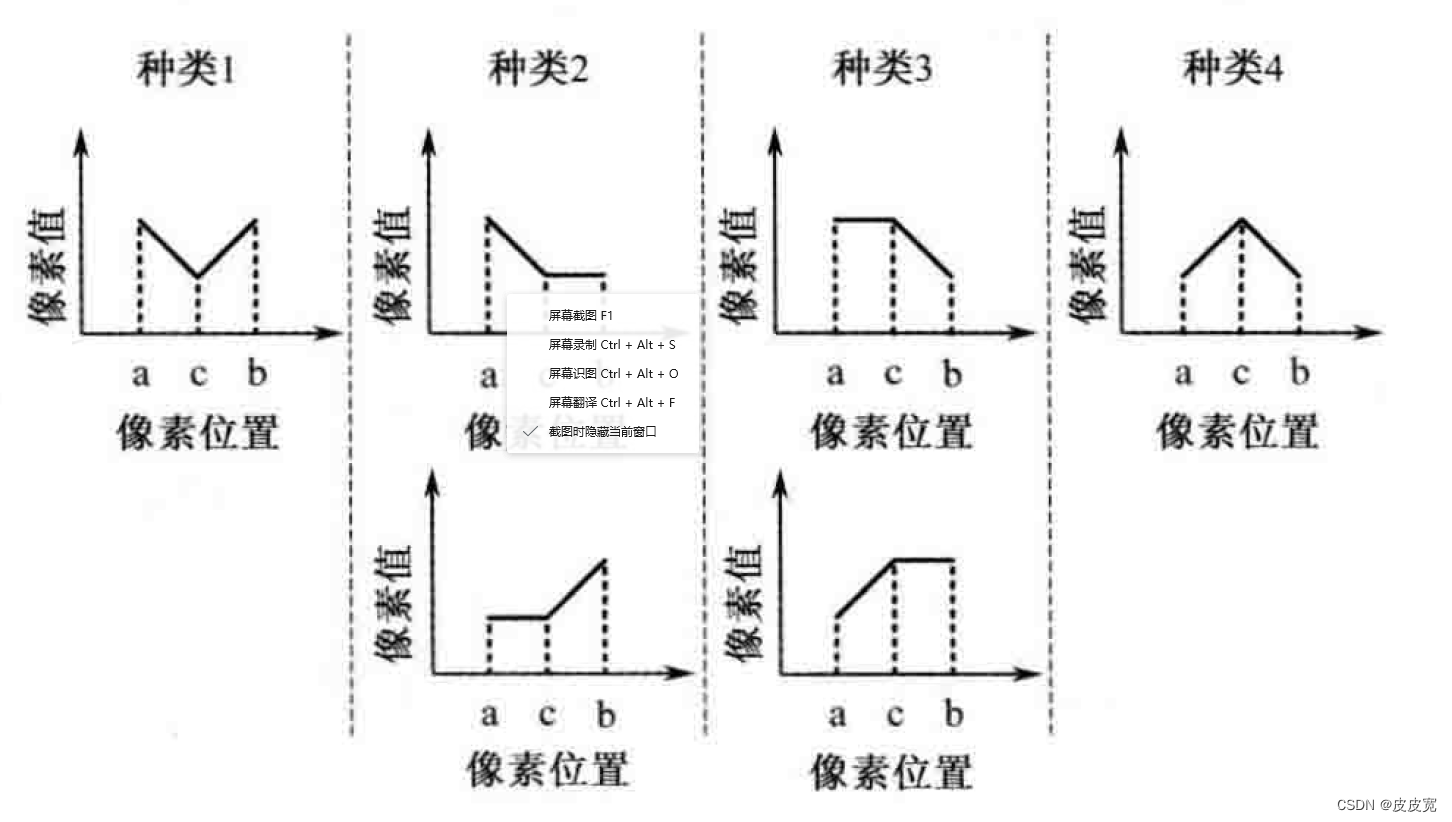
Xu Zhou等人在《A boundary condition based deconvolution framework for image deblurring》提及，由于原文写的公式比较复杂不好理解，所以就不赘述了，其实核心就是外部边界区域内的某个像素点的灰度等于距离其最近图像内像素点的灰度的大小。由于分界线是水平或者垂直的，那就更简单了，假设把外部边界分为8个区域：

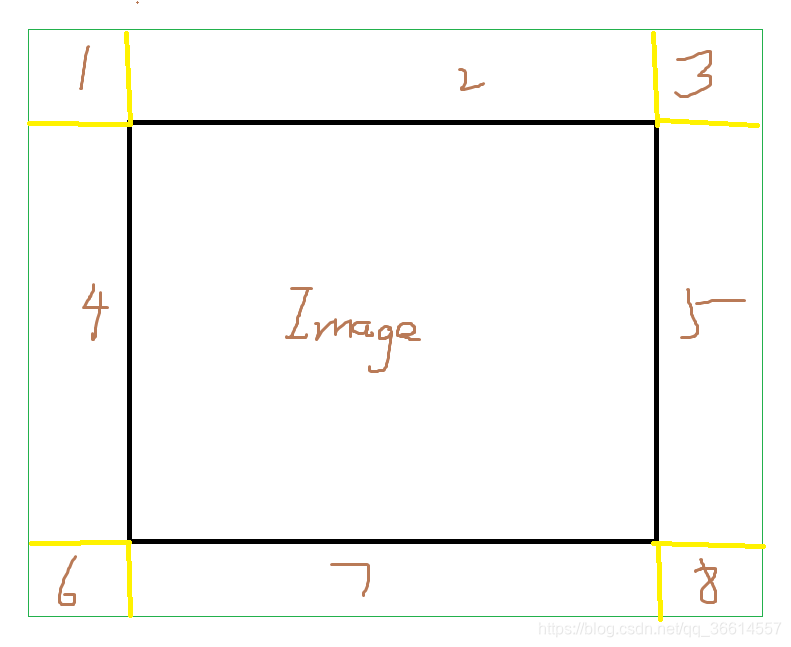
即：1中所有像素值等于内部图像最左上角的像素值，3、6、8类似分别对应右上角、左下角、右下角；2、7内每个像素的的像素值为内部图像同列的最上方/下方的像素值；4、5内每个像素的的像素值为内部图像同行的最左方/右方的像素值。

2.Undetermined BC

在《Image and depth from a conventional camera with a coded aperture》中出现，该BC假设使原图像x扩充为带假设边界条件的扩充图像xe的函数P（成为边界条件矩阵）为未知的，并且P的核为0.

3.平滑边界方法

来自于《Reducing boundary artifacts in image deconvolution》。为了节省时间和防止自绘的图片太过于辣眼睛，直接使用论文里的部分图像和公式。

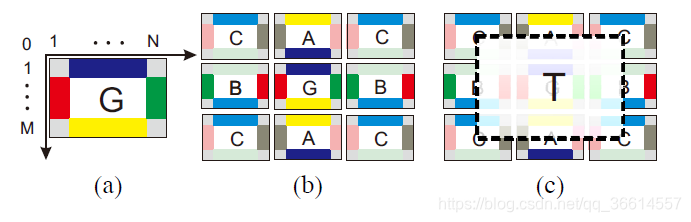
如图所示，G为M*N大小的原始图像图像，作者分别假设了和G等大小的A、B、C，A的底部、顶部分别与G的顶部、底部尽可能相似；B的左部、右部分别与G的右部、左部尽可能相似；C的底部、顶部分别与B的顶部、底部尽可能相似；C的左部、右部分别与A的右部、左部尽可能相似；如(b)所示，相同颜色的为相似部分，最后的扩充图像为(c)图的T。

作者先假设边界宽度为 $\alpha$ （在此文中，边界宽度与最后扩充的边界宽度不同），用A'表示A经过上下边界扩充后的图像，大小为(M+2 $\alpha$ )*N，并且满足：

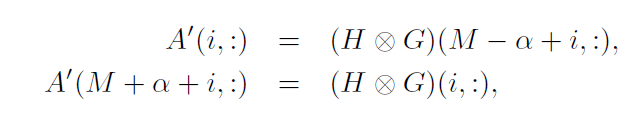
A’上式计算区域即A的边界区域。i取值为1到 $\alpha$ 。等式右侧左部表示原始图像与高斯滤波器滤波后的平滑图像。A通过最小化下式得到：

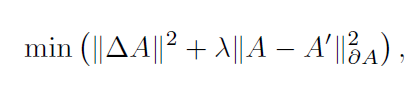
$\Delta A$ 表示对A进行拉普拉斯滤波， $\partial \alpha$ 表示外部边界，上述公式表示在满足A的二阶梯度值的平方和与A‘边界差异值的平方和最小的情况下的最优解即最后的A值。B、C同理，注意B’为M*(N+2 $\alpha$ )，C‘为(M+2 $\alpha$ )*(N+2 $\alpha$ )。B’的边界为第1到 $\alpha$ 列和第N+ $\alpha$ +1到第N+2 $\alpha$ 列，C的边界区域第1到 $\alpha$ 列和第N+ $\alpha$ +1到第N+2 $\alpha$ 列、第1到 $\alpha$ 行和第N+ $\alpha$ +1到第N+2 $\alpha$ 行。

4.渐进边界条件

源自《基于稀疏正则化和渐近边界假设的运动模糊图像盲复原》。设扩充边界宽度为n，图像大小为H*W，作者把扩充图像分为8个部分，并且1~4区域按照从内往外的方向扩充：

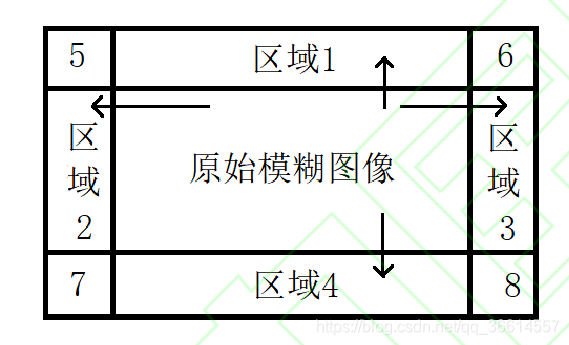
扩充方法如下：（y表示原始模糊图像）

对于区域1：

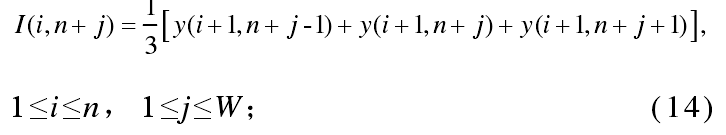
即对于某个像素，其灰度值等于下方、左下和右下三个像素灰度值的平均，特殊的，如果位于边界，则是三个像素位于像素内的了两个像素的平均。

对于区域2：

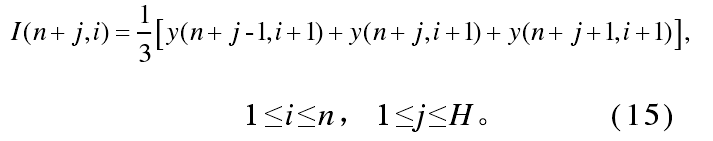
区域3和4类似。然后对区域1~4进行渐进化处理，即从内往外越来越暗：

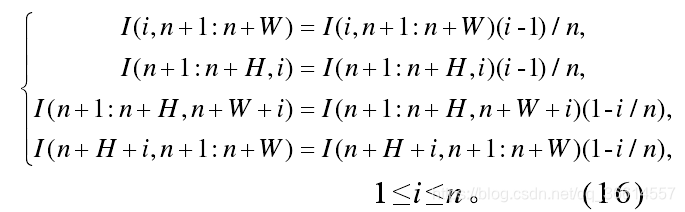
对于5~8区域，按如下方向扩充：

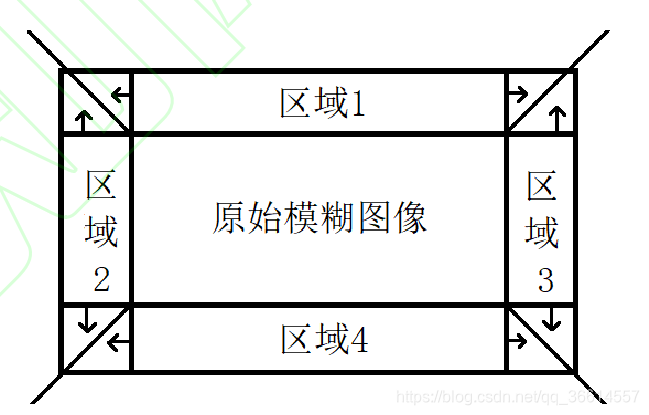
以区域5为例，下三角某像素的灰度值等于区域2同列最近的像素的灰度值，上三角等于同行最近的灰度值。位于对角线上的像素为同行和同列的均值。

Repeated BC效果如下：

渐进边界条件效果如下：

但是平滑边界方法我理解起来比较模糊，由于实现起来有点晕，在这里贴上原文对A‘和 $\partial \alpha$ 的定义：

We expand block A by a few pixels vertically, which results in a larger square block A’ containing A and its outer-border ∂A. ∂A is defined as......

之后的内容就是第一个公式。困惑的问题在于：如果A是H*W的，A的外部边界尽可能地和A‘的最开始alpha行和最后alpha行相似，而A的梯度尽可能地小，那么。。。使得式子出现最小值地情况不就是外部边界就是A’那几行，而内部图像的H*W全零？因为计算梯度只计算内部的。而如果是计算A+外部边界的梯度，那么可以理解并且结果是理想的，但是就不太符合公式里的说法了，因为公式写的是 $\Delta A$ ,而不是 ${\Delta A}'$ 。但是如果是只对A的话那就毫无意义了。公式里最小化函数右侧子式的右下角的区域限定为 $\partial A$ ，如果我理解没错的话就是指的是A的外部边界和A’的那几行，而不是A和A‘各自的外部边界区域相等。在这就假设是对A和外部边界求梯度吧，但是最后结果只要A中心图像那一块。

___________________________________________________

2021.7.27之前扯犊子自己复现的低级版本删除了

原因是从极通道的图像去模糊的源码里找到Liu的边界条件的代码了

需要的请移步

找不到之前的图，随便找个图贴一下效果吧~

代码部分：

1.Repeated BC

x=rgb2gray(imread('tt.jpg'));
[N1,N2]=size(x);
% [M1,M2]=size(Psf);
M1=127;
M2=127;
m1=(M1-1)/2;
m2=(M1-1)/2;
%Repeated BCxe=zeros(N1+2*m1,N2+2*m2);
for i=1:N1+2*m1for j=1:N2+2*m2if i<=m1 if j<=m1%区域1xe(i,j)=x(1,1);elseif j<=m1+N2 %区域2xe(i,j)=x(1,j-m1);else %区域3xe(i,j)=x(1,N2);endelseif i<=m1+N1 %区域4if j<=m1xe(i,j)=x(i-m1,1);elseif j<=m1+N2%内部图像区域xe(i,j)=x(i-m1,j-m1);else%区域5xe(i,j)=x(i-m1,N2);endelseif j<=m1%区域6xe(i,j)=x(N1,1);elseif j<=m1+N2%区域7xe(i,j)=x(N1,j-m1);else%区域8xe(i,j)=x(N1,N2);end   endend
end

4.渐进边缘条件：

%title:《Blind Restoration of Motion Blurred Images Based on Sparse Regularization and Asymptotic Boundary Hypothesis》
%基于稀疏正则化和渐近边界假设的运动模糊图像盲复原 f=rgb2gray(imread('tt.jpg'));
[H,W]=size(f);
% psf=load('psf_304.txt');
% Psf=psf./sum(sum(psf));
% y=imfilter(f,Psf,'conv'); 
% [n,n2]=size(psf);%模糊核大小
n=128;%宽度
I=zeros(H+2*n,W+2*n);
I(n+1:n+H,n+1:n+W)=f;
%area 1
for i=n:-1:1%注意从内向外，在area1为从下到上递减for j=n+1:n+Wif j==n+1I(i,j)=(I(i+1,j)+I(i+1,j+1))/2;%如果位于最左侧elseif j==n+WI(i,j)=(I(i+1,j)+I(i+1,j-1))/2;%如果位于最右侧elseI(i,j)=(I(i+1,j-1)+I(i+1,j)+I(i+1,j+1))/3;%其余情况endend
end
%area 4
for i=n+H+1:n+H+n%注意从内向外，在area1为从上到下递增for j=n+1:n+Wif j==n+1I(i,j)=(I(i-1,j)+I(i-1,j+1))/2;elseif j==n+WI(i,j)=(I(i-1,j)+I(i-1,j-1))/2;elseI(i,j)=(I(i-1,j-1)+I(i-1,j)+I(i-1,j+1))/3;endend
end
%area 2
for j=n:-1:1for i=n+1:n+Hif i==n+1I(i,j)=(I(i,j+1)+I(i+1,j+1))/2;elseif i==n+WI(i,j)=(I(i,j+1)+I(i-1,j+1))/2;elseI(i,j)=(I(i-1,j+1)+I(i,j+1)+I(i+1,j+1))/3;endend
end
%area 3
for j=n+W+1:n+W+nfor i=n+1:n+Hif i==n+1I(i,j)=(I(i,j-1)+I(i+1,j-1))/2;elseif i==n+WI(i,j)=(I(i,j-1)+I(i-1,j-1))/2;elseI(i,j)=(I(i-1,j-1)+I(i,j-1)+I(i+1,j-1))/3;endend
end
for i=1:n%渐进缩放I(i,n+1:n+W)=I(i,n+1:n+W)*(i-1)/n;I(n+1:n+H,i)=I(n+1:n+H,i)*(i-1)/n;I(n+1:n+H,n+W+i)=I(n+1:n+H,n+W+i)*(n-i)/n;I(n+H+i,n+1:n+W)=I(n+H+i,n+1:n+W)*(n-i)/n;
end% area 5
for i=1:nfor j=1:nif i<j %上三角I(i,j)=I(i,n+1);elseif i>j I(i,j)=I(n+1,j);elseI(i,j)=(I(i,n+1)+I(n+1,j))/2;endend
end
%area  8
for i=n+H+1:n+H+nfor j=n+W+1:n+W+nif i-H<j-W %上三角I(i,j)=I(n+H,j);elseif i-H>j-W I(i,j)=I(i,n+W);elseI(i,j)=(I(i,n+W)+I(n+H,j))/2;endend
end
%area 6
for i=1:nfor j=n+W+1:n+W+nif i+(j-W-n)<nI(i,j)=I(i,n+W);elseif i+(j-W-n)>nI(i,j)=I(n+1,j);elseI(i,j)=(I(i,n+W)+I(n+1,j))/2;endend
end
%area 7
for i=n+H+1:n+H+nfor j=1:nif j+(i-H-n)<nI(i,j)=I(n+H,j);elseif j+(i-H-n)>nI(i,j)=I(i,n+1);elseI(i,j)=(I(i,n+1)+I(n+H,j))/2;endend
end
I=uint8(I);

3.平滑边缘方法：见 ECP（基于极通道的图像去模糊）代码