1、二分查找算法（非递归）

二分查找算法(非递归)介绍

1. 查找算法里面学习了二分查找算法，是使用递归的方式，其实可以使用非递归的方法。
2. 二分查找法只适用于从有序的数列中进行查找(比如数字和字母等)，将数列排序后再进行查找
3. 二分查找法的运行时间为对数时间O(log2 n) ，即查找到需要的目标位置最多只需要log2 n步，假设从[0,99]的队列(100个数,即n=100)中寻到目标数30,则需要查找步数为log2100, 即最多需要查找7次(2⁶< 100 <2⁷)

二分查找算法(非递归)代码实现

数组{1,3,8, 10, 11, 67, 100},编程实现二分查找，要求使用非递归的方式完成.

private static int binarySearch(int[] arr,int value) {int left = 0;int right = arr.length-1;while(left<=right) {int mid = (right-left)/2+left;if(arr[mid]==value) {return mid;}else if(arr[mid]>value) {right = mid-1;}else {left = mid+1;}}return -1;}

2、分治算法

分治算法介绍

1. 分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题…直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换…
2. 分治算法可以求解的一些经典问题
   ✔二分搜索
   ✔大整数乘法
   ✔棋盘覆盖
   ✔归并排序
   ✔快速排序
   ✔线性时间选择
   ✔最接近点对问题.
   ✔循环赛日程表
   ✔汉诺塔

分治算法的基本步骤

分治法在每一层递归上都有三个步骤:

1. 分解:将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
2. 解决: 若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
3. 合并:将各个子问题的解合并为原问题的解。
   

分治算法最佳实践汉诺塔

➢汉诺塔的传说
汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一-根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一-次只能移动一个圆盘。假如每秒钟一次，共需多长时间呢?移完这些金片需要5845.54亿年以上，太阳系的预期寿命据说也就是数百亿年。真的过了5845.54亿年，地球上的一切生命，连同梵塔、庙宇等，都早已经灰飞烟灭。

➢汉诺塔游戏的演示和思路分析:

1. 如果是有一个盘， A->C
   如果我们有n>=2情况，我们总是可以看做是两个盘：
   1.最下边的盘
   2.上面的盘
2. 先把最上面的盘A->B
3. 把最下边的盘A->C .
4. 把B塔的所有盘从B->C

➢汉诺塔 游戏的代码实现:

package com.xhl.composite;public class Hanoitower {private static int count=0;public static void main(String[] args) {// TODO Auto-generated method stubhanoitower(3,'A','B','C');}//分治private static void hanoitower(int num, char a, char b, char c) {if(num>1) {hanoitower(num-1, a, c, b);}System.out.println("第"+num+"个盘从"+a+"--->"+c);if(num>1) {hanoitower(num-1, b, a, c);}}}

3、动态规划

动态规划算法介绍

1. 动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法
2. 动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
3. 与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。(即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解 )
4. 动态规划可以通过填表的方式来逐步推进，得到最优解.

应用场景——背包问题

背包问题:有一个背包，容量为4磅，现有如下物品：

物品	重量	价格
吉他（G）	1	1500
音响（S）	4	3000
电脑（L）	3	2000

1. 要求达到的目标为装入的背包的总价值最大，并且重量不超出
2. 要求装入的物品不能重复

思路分析：

1. 背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品，如何选择物品放入背包使物品的价值最大。其中又分01背包和完全背包(完全背包指的是:每种物品都有无限件可用)
2. 这里的问题属于01背包，即每个物品最多放一个。而无限背包可以转化为01背包。
3. 算法的 主要思想，利用动态规划来解决。每次遍历到的第i个物品，根据w[i]和v[i]来确定是否需要将该物品放入背包中。即对于给定的n个物品，设v[i、 w[i]分别为第i个物品的价值和重量, C为背包的容量。再令v[i]lj]表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果:
   
   

package com.xhl.dynamic;import java.util.Arrays;public class KnapsackProblem {public static void main(String[] args) {String[] goods = {"吉他","音箱","电脑"};int[] weight = {1,4,3};//重量int[] val = {1500,3000,2000};//价值int m = 4;//背包的容量int[][] path = new int[goods.length][m+1];int[] maxval = new int[m+1];System.out.println("============完全背包=============");//完全背包path = new int[goods.length][m+1];for(int i=0;i<goods.length;i++) {for(int j=0;j<=m;j++) {if(weight[i]<=j) {//此时加入的物品重量小于等于限制重量int v = maxval[j-weight[i]]+val[i];//maxval[j] = v>maxval[j]?v:maxval[j];if(v>maxval[j]) {path[i][j]=1;maxval[j]=v;}}}System.out.println(Arrays.toString(maxval));}System.out.println(maxval[m]);int p=goods.length-1;int q=m;while(p>=0&&q>=0) {if(path[p][q]==1) {System.out.printf(goods[p]+"\t");q -= weight[p];}else {p--;}}System.out.println();System.out.println("============01背包=============");int[][] arr = new int[2][m+1];//01背包for(int i=0;i<goods.length;i++) {for(int j=0;j<=m;j++) {int k = i==0?1:(i-1)%2;if(weight[i]<=j) {//此时加入的物品重量小于等于限制重量int v = arr[k][j-weight[i]]+val[i];//arr[i%2][j] = v>arr[k][j]?v:arr[k][j];if(v>arr[k][j]) {path[i][j]=1;arr[i%2][j] = v;}else {arr[i%2][j] = arr[k][j];}}else {arr[i%2][j] = arr[k][j];}}System.out.println(Arrays.toString(arr[i%2]));}System.out.println(arr[(goods.length-1)%2][m]);p=goods.length-1;q=m;while(p>=0&&q>=0) {if(path[p][q]==1) {System.out.printf(goods[p]+"\t");q -= weight[p];}p--;}}}

4、KMP算法*next数组生成

KMP 算法介绍

1. KMP是一个解决模式串在文本串是否出现过，如果出现过，最早出现的位置的经典算法
2. Knuth-Morris-Pratt 字符串查找算法，简称为“KMP 算法”，常用于在一个文本串S内查找一个模式串P的出现位置，这个算法由Donald Knuth、Vaughan Pratt、James H. Morris 三人于1977年联合发表，故取这3人的姓氏命名此算法.
3. KMP 方法算法就利用之前判断过信息，通过一个next数组，保存模式串中前后最长公共子序列的长度，每次回溯时，通过next数组找到，前面匹配过的位置，省去了大量的计算时间
4. 参考资料

应用场景——字符串匹配问题

➢字符串匹配问题: :

1. 有一个字符串str1="“千山鸟飞绝鸟飞绝飞绝绝万径人踪灭”"，和一个子串str2="鸟飞绝飞绝绝”
2. 现在要判断str1 是否含有str2, 如果存在，就返回第一次出现的位置，如果没有，则返回-1

暴力匹配算法

如果用暴力匹配的思路，并假设现在strl匹配到i位置，子串str2 匹配到j位置，则有:

1. 如果当前字符匹配成功(即str1[i]== str2[j]) ，则i++，j++， 继续匹配下一个字符
2. 如果失配 (即str1[i]!= str2[j])，令i=i-(j-1)， j=0。相当于每次匹配失败时，i回溯，j被置为0。
3. 用暴力方法解决的话就会有大量的回溯，每次只移动一位，若是不匹配，移动到下一位接着判断，浪费了大量的时间。(不可行!)
   
   
   
   
   
   

KMP算法

package com.xhl.composite;public class KMPAlgorithm {public static void main(String[] args) {// TODO Auto-generated method stubString str1 = "BBC ABCDAB ABCDABCDABDE";String str2 = "ABCDABD";int[] next = kempNext(str2);int index = kmpSearch(str1,str2,next);System.out.println(index);System.out.println(str1.charAt(index));}private static int kmpSearch(String str1, String str2, int[] next) {int i=0,j=0;while(i<str1.length()&&j<str2.length()){if(j==-1||str1.charAt(i)==str2.charAt(j)) {i++;j++;}else {j=next[j];}}if(j==str2.length()) {return (i-j);}else {return -1;}}//获取到子串的部分匹配值表private static int[] kempNext(String dest) {//next保存部分匹配值int[] next = new int[dest.length()];int k=-1;int j=0;next[0]=-1;//下面这段神仙代码只可意会不可言传，自行理解，最后自己试着走一遍就懂了while(j<dest.length()-1) {if(k==-1||dest.charAt(k)==dest.charAt(j)) {k++;j++;next[j]=k;}else {k=next[k];}}return next;}}

改进

显然，当我们上边的算法得到的next数组应该是[ -1，0，0，1 ]
所以下一步我们应该是把j移动到第1个元素咯：

不难发现，这一步是完全没有意义的。因为后面的B已经不匹配了，那前面的B也一定是不匹配的，同样的情况其实还发生在第2个元素A上。
显然，发生问题的原因在于 t[j] == t[next[j]]。
所以我们需要谈价一个判断：

//改进后==========================================// 获取到子串的部分匹配值表private static int[] kempNext1(String dest) {// next保存部分匹配值int[] next = new int[dest.length()];int k = -1;int j = 0;next[0] = -1;// 下面这段神仙代码只可意会不可言传，自行理解，最后自己试着走一遍就懂了while (j < dest.length() - 1) {if (k == -1 || dest.charAt(k) == dest.charAt(j)) {k++;j++;if(dest.charAt(k) == dest.charAt(j)) {next[j]=next[k];}else {next[j] = k;}} else {k = next[k];}}return next;}

5、贪心算法

贪心算法介绍.

1. 贪婪算法(贪心算法)是指在对问题进行求解时，在每–步选择中都采取最好或者最优(即最有利)的选择，从而希望能够导致结果是最好或者最优的算法
2. 贪婪 算法所得到的结果不一定是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果

贪心算法最佳应用——集合覆盖

1. 假设存在如下表的需要付费的广播台，以及广播台信号可以覆盖的地区。 如何选择最少的广播台，让所有的地区都可以接收到信号
   
2. 思路分析:
   ➢如何找出覆盖所有地区的广播台的集合呢，使用穷举法实现，列出每个可能的广播台的集合，这被称为幂集。假设总的有n个广播台，则广播台的组合总共有
   2ⁿ -1 个,假设每秒可以计算10个子集，如图:
   

➢使用贪婪算法，效率高:

1. 目前并没有算法可以快速计算得到准备的值，使用贪婪算法，则可以得到非常接近的解，并且效率高。选择策略上，因为需要覆盖全部地区的最小集合:
2. 遍历所有的广播电台，找到一个覆盖了最多未覆盖的地区的电台(此电台可能包含一些已覆盖的地区，但没有关系)
3. 将这个电台加入到一个集合中(比如ArrayList),想办法把该电台覆盖的地区在下次比较时去掉。
4. 重复第1步直到覆盖了全部的地区

package com.xhl.composite;import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;public class GreedyAlgorithm {public static void main(String[] args) {//创建广播电台，放到mapHashMap<String, HashSet<String>> broadcasts = new HashMap<String, HashSet<String>>();//将各个电台放到broadcastHashSet<String> hashSet1 = new HashSet<String>();hashSet1.add("北京");hashSet1.add("上海");hashSet1.add("天津");HashSet<String> hashSet2 = new HashSet<String>();hashSet2.add("广州");hashSet2.add("北京");hashSet2.add("深圳");HashSet<String> hashSet3 = new HashSet<String>();hashSet3.add("成都");hashSet3.add("上海");hashSet3.add("杭州");HashSet<String> hashSet4 = new HashSet<String>();hashSet4.add("上海");hashSet4.add("天津");HashSet<String> hashSet5 = new HashSet<String>();hashSet5.add("杭州");hashSet5.add("大连");broadcasts.put("K1", hashSet1);broadcasts.put("K2", hashSet2);broadcasts.put("K3", hashSet3);broadcasts.put("K4", hashSet4);broadcasts.put("K5", hashSet5);HashSet<String> allAreas = new HashSet();allAreas.add("北京");allAreas.add("上海");allAreas.add("天津");allAreas.add("广州");allAreas.add("深圳");allAreas.add("成都");allAreas.add("杭州");allAreas.add("大连");//创建ArrayList,存放选择的电台集合ArrayList<String> selects = new ArrayList();//定义一个临时的集合，在遍历的过程中，存放遍历过程中的电台覆盖的地区和当前还没有覆盖的地区的交集HashSet<String> tempSet = new HashSet();//定义给maxKey，保存在一次遍历过程中，能够覆盖最大未覆盖的地区对应的电台的keyString maxKey = null;//如果maxKey不为null,则会加入到selectswhile(allAreas.size()!=0) {// 如果alraes不为0,则表示还没有覆盖到所有的地区maxKey = null;for(String key : broadcasts.keySet()) {tempSet.clear();tempSet.addAll(broadcasts.get(key));tempSet.retainAll(allAreas);if(tempSet.size()>0&&(maxKey==null||tempSet.size()>broadcasts.get(maxKey).size())) {maxKey = key;}}if(maxKey!=null) {selects.add(maxKey);allAreas.removeAll(broadcasts.get(maxKey));}}System.out.println(selects);}}

总结

1. 贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果
2. 比 如上题的算法选出的是K1,K2, K3,K5，符合覆盖了全部的地区
3. 但是我们发现 K2, K3,K4,K5也可以覆盖全部地区，如果K2的使用成本低于K1,那么我们上题的K1, K2, K3,K5虽然是满足条件，但是并不是最优的

6、普里姆算法

应用场景——修路问题

➢看一个应用场景和问题:

最小生成树

修路问题本质就是就是最小生成树问题，先介绍一下最小生成树(Minimum Cost Spanning Tree),简称MST.给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小，这叫最小生成树

1. N个顶点，一定有N-1条边
2. 包含全部顶点.
3. N-1 条边都在图中
4. 举例说明(如图:)
5. 求最小生成树算法主要是普里姆算法和克鲁斯卡尔算法
   

普里姆算法介绍

普利姆(Prim)算法求最小生成树，也就是在包含n个顶点的连通图中，找出只有(n- 1)条边包含所有n个顶点的连通子图，也就是所谓的极小连通子图

普利姆的算法如下:

1. 设G=(V,E)是连通网，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边的集合
2. 若从顶点u开始构造最小生成树，则从集合V中取出顶点u放入集合U中，标记项点v的visited[u]=1
3. 若集合U中顶点ui与集合V中的顶点vj之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点vj加入集合U中，将边(ui,vj) 加入集合D中，标记visited[vj]=1
4. 重复步骤②，直到U与V相等，即所有顶点都被标记为访问过，此时D中有n-1条边
5. 图解普利姆算法
   

普里姆算法最佳实践(修路问题)

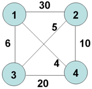
1. 有胜利乡有7个村庄(A, B, C, D,E,F,G)，现在需要修路把7个村庄连通
2. 各个村庄的距离用边线表示(权)，比如A-B距离5公里
3. 问: 如何修路保证各个村庄都能连通，并且总的修建公路总里程最短?
   以从A出发为例子
   ABCDEFG分别用0-6表示
   
   

package com.xhl.composite;public class MGraph {int verxs;//表示图的节点个数char[] data;//存放结点数据int[][] weight;//存放边public MGraph(int verxs) {this.verxs = verxs;data = new char[verxs];weight = new int[verxs][verxs];}
}

package com.xhl.composite;import java.util.Arrays;public class MinTree {//创建图的邻接矩阵/*@param graph图对象@param verxs图对应的顶点个数@param data图的各个顶点的值@param weight 图的邻接矩阵*/public void createGraph(MGraph graph , int verxs,char[] data,int[][] weight) {int i,j;for(i=0;i<verxs;i++) {graph.data[i]=data[i];for(j=0;j<verxs;j++) {graph.weight[i][j]=weight[i][j];}}}//显示图的邻接矩阵public void showGraph(MGraph graph) {for(int[] w:graph.weight) {System.out.println(Arrays.toString(w));}}/*编写prim算法，得到最小生成树@param graph图@param v表示从图的第几个顶点开始生成'A'->0 'B'->1...*/public void prim(MGraph graph,int v) {//记录以i为终点的边的最小权值;lowcost[i]=-1,表示终点i已加入生成树int[] lowcost = new int[graph.verxs];//记录对应lowcost[i]的起点；mst[i]=-1时，表示起点i已加入生成树int[] mst = new int[graph.verxs];for(int i=0;i<graph.verxs;i++) {lowcost[i]=graph.weight[v][i];mst[i] = v;}mst[v] = -1;//顶点v已加入生成树lowcost[v] = -1;for(int k=0;k<graph.verxs-1;k++) {int min = PrimDemo.max;//最小权值置为无穷大int minid = -1;//而边的终点下标置为0for(int i=0;i<graph.verxs;i++) {//查找当前的边的最小权值及对应的终点下标if(lowcost[i]<min&&lowcost[i]!=-1) {//还未加入生成树min = lowcost[i];minid = i;}}System.out.println(graph.data[mst[minid]]+"--->"+graph.data[minid]+"\t"+min);lowcost[minid]=-1;//minid顶点加入生成树mst[minid]=-1;for(int i=0;i<graph.verxs;i++) {if(mst[i]!=-1&&graph.weight[minid][i]<lowcost[i]) {lowcost[i]=graph.weight[minid][i];//更新权值信息mst[i]=minid;//更新最小权值边的起点}}System.out.println(Arrays.toString(mst));System.out.println(Arrays.toString(lowcost));}}}

package com.xhl.composite;public class PrimDemo {public static final int max = 10000;public static void main(String[] args) {char[] data = new char[] {'A','B','C','D','E','F','G'};int verxs = data.length;//邻接矩阵表示int[][] weight = new int[][] {{max,5,7,max,max,max,2},{5,max,max,9,max,max,3},{7,max,max,max,8,max,max},{max,9,max,max,max,4,max},{max,max,8,max,max,5,4},{max,max,max,4,5,max,6},{2,3,max,max,4,6,max}};MGraph graph = new MGraph(verxs);MinTree minTree = new MinTree();minTree.createGraph(graph, verxs, data, weight);minTree.showGraph(graph);minTree.prim(graph, 0);}
}

7、克鲁斯卡尔算法

克鲁斯卡尔算法基本介绍

1. 克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法。
2. 基本思想:按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路
3. 具体做法: 首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森;林中不产生回路，直至森林变成一棵树为止

克鲁斯卡尔算法图解说明

以城市公交站问题来图解说明克鲁斯卡尔算法的原理和步骤:

克鲁斯卡尔最佳实践公交站问题

package com.xhl.kruskal;public class EDate implements Comparable<EDate>{char start;//边的一个点int startid;char end;//边的另一个点int endid;int weight;public EDate(int startid,int endid, char start, char end, int weight) {super();this.startid=startid;this.endid = endid;this.start = start;this.end = end;this.weight = weight;}@Overridepublic String toString() {// TODO Auto-generated method stubreturn "<"+start+","+end+">="+weight;}@Overridepublic int compareTo(EDate arg0) {return this.weight-arg0.weight;}}

package com.xhl.kruskal;import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;public class MinTree {//存放边的集合private static List<EDate> edges = new ArrayList();public MinTree(int[][] weight,char[] data,int vertexs) {for(int i=0;i<vertexs-1;i++) {for(int j=i+1;j<vertexs;j++) {edges.add(new EDate(i,j,data[i], data[j], weight[i][j]));}}Collections.sort(edges);for(EDate e:edges) {System.out.println(e);}System.out.println();}public void kruskal(int vertexs) {int[] all = new int[vertexs];for(int i=0;i<vertexs;i++) {all[i]=-1;//表示未标记}all[edges.get(0).startid]=edges.get(0).startid;int count=1;for(EDate e:edges) {if(all[e.endid]!=-1&&all[e.startid]!=-1) {if(all[e.endid]!=all[e.startid]) {//来自两个不同的数System.out.println(e);for(int i=0;i<vertexs;i++) {//进行染色if(all[i]==all[e.endid]) {all[i]=all[e.startid];}}count++;}}else if(all[e.endid]==-1&&all[e.startid]==-1) {System.out.println(e);all[e.startid]=all[e.endid]=e.startid;count++;}else if(all[e.endid]!=-1&&all[e.startid]==-1){System.out.println(e);all[e.startid]=all[e.endid];count++;}else if(all[e.endid]==-1&&all[e.startid]!=-1) {System.out.println(e);all[e.endid]=all[e.startid];count++;}if(count==vertexs) {break;}}}
}

package com.xhl.kruskal;public class KruskalDemo {private static final int max = Integer.MAX_VALUE;public static void main(String[] args) {char[] data = new char[] {'A','B','C','D','E','F','G'};int vertexs = data.length;//邻接矩阵表示int[][] weight = new int[][] {{max,5,7,max,max,max,2},{5,max,max,9,max,max,3},{7,max,max,max,8,max,max},{max,9,max,max,max,4,max},{max,max,8,max,max,5,4},{max,max,max,4,5,max,6},{2,3,max,max,4,6,max}};MinTree mTree = new MinTree(weight, data, vertexs);mTree.kruskal(vertexs);;}
}

8、迪杰斯特拉算法

迪杰斯特拉(Dijkstra)算法介绍.

迪杰斯特拉(Djkstra)算法是典型最短路径算法，用于计算一个结点到其他结点的最短路径。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

迪杰斯特拉(Dijkstra)算法过程

1. 设置出发顶点为v，顶点集合V{v1，v2，…，vi }, v到V中各顶点的距离构成距离集合Dis, Dis{d1，d2，…，di }, Dis集合记录着v到图中各顶点的距离(到自身可以看作0，v到vi距离对应为di)
   

2. 从Dis中选择值最小的di并移出Dis集合，同时移出V集合中对应的顶点vi，此时的v到vi即为最短路径
   

3. 更新Dis集合， 更新规则为:比较v到V集合中顶点的距离值，与v通过vi到V集合中顶点的距离值，保留.值较小的一个(同时也应该更新顶点的前驱节点为vi,表明是通过vi到达的)

4. 重复执行两步骤，直到最短路径顶点为目标顶点即可结束

迪杰斯特拉(Dijkstra)算法最佳应用——最短路径

package com.xhl.Dijkstra;import java.util.Arrays;
import java.util.Stack;public class Dijkstra {private static final int max = 10000;private static int[] previous;private static int[] minPaths;public static void main(String[] args) {char[] data = new char[] {'A','B','C','D','E','F','G'};int vertexs = data.length;//邻接矩阵表示int[][] weight = new int[][] {{max,5,7,max,max,max,2},{5,max,max,9,max,max,3},{7,max,max,max,8,max,max},{max,9,max,max,max,4,max},{max,max,8,max,max,5,4},{max,max,max,4,5,max,6},{2,3,max,max,4,6,max}};dijkstra(weight, vertexs, 0);System.out.println(Arrays.toString(previous));System.out.println(Arrays.toString(minPaths));for(int i=0;i<vertexs;i++) {show(i,data);}}public static void show(int v,char[] data) {Stack stack = new Stack<>();int path = minPaths[v];stack.push(v);while(previous[v]!=-1) {stack.push(previous[v]);v=previous[v];}while(!stack.empty()) {System.out.print(data[(int) stack.pop()]+"-->");}System.out.println(path);}public static void dijkstra(int[][] weight,int vertexs,int v) {previous = new int[vertexs];minPaths = new int[vertexs];int[] flag = new int[vertexs];int min = 0;//坐标for(int i=0;i<vertexs;i++) {minPaths[i]=weight[v][i];min= minPaths[min]>minPaths[i]?i:min;previous[i]=v;}previous[v]=-1;//起始minPaths[v]=0;flag[v]=1;//标记while(true) {	flag[min]=1;int index = min;min = -1;boolean tag=true;for(int j=0;j<vertexs;j++) {if(flag[j]!=1) {tag =false;int k = minPaths[index]+weight[index][j];if(k<minPaths[j]) {minPaths[j]=k;previous[j]=index;}if(min == -1) {min = j;}else {min = minPaths[j]<minPaths[min]?j:min;}}}if(tag) {break;}}}
}

9、弗洛伊德算法

弗洛伊德(Floyd)算法介绍

1. 和Dijkstra算法-一样，弗洛伊德(Floyd)算法也是-种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978 年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特●弗洛伊德命名
2. 弗洛 伊德算法(Floyd)计算图中各个顶点之间的最短路径
3. 迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径。
4. 弗洛伊德算法VS迪杰斯特拉算法:迪杰斯特拉算法通过选定的被访问顶点，求出从出发访问顶点到其他顶点的最短路径;弗洛伊德算法中每一个顶点都是出发访问点，所以需要将每一个顶点看做被访问顶点，求出从每.一个顶点到其他顶点的最短路径。

弗洛伊德(Floyd)算法图解分析

1. 设置顶点 vi到顶点vk的最短路径已知为Lik,顶点vk到vj的最短路径已知为Lkj,顶点vi到vj的路径为Lij,则vi到vj的最短路径为: min((Lik+Lkj),Lij)， vk的取值为图中所有顶点，则可获得vi到vj的最短路径
2. 至于vi到vk的最短路径Lik或者vk到vj的最短路径Lkj，是以同样的方式获
   
   
   
   

弗洛伊德算法应用——最短路径

package com.xhl.Floyd;import java.util.Arrays;public class Graph {private char[] vertex;//存放顶点数组private int[][] dis;//保存从各个顶点出发到其他顶点的距离，最后结果要保留在该数组private int[][] pre;//保存达到目标顶点的前驱节点public Graph(char[] vertex, int[][] dis, int length) {super();this.vertex = vertex;this.dis = dis;this.pre = new int[length][length];for(int i=0;i<length;i++) {Arrays.fill(pre[i], i);}}//显示pre数组和dis数组public void show() {for(int[] i:dis) {System.out.println(Arrays.toString(i));}System.out.println();for(int[] i:pre) {for(int j:i) {System.out.print(vertex[j]+"\t");}System.out.print("\n");}}public void floyd() {int len = 0;//保存距离//对中间顶点遍历，k就是中间顶点的下标[A,B, C,D, E, F, G]for(int k=0;k<dis.length;k++) {//从i顶点开始出发[A,B,C,D,E, F, G]for(int i=0;i<dis.length;i++) {//到达j顶点//[A,B,C,D, E, F, G]for(int j=0;j<dis.length;j++) {len = dis[i][k]+dis[k][j];if(len<dis[i][j]) {dis[i][j]=len;pre[i][j]=pre[k][j];}}}}}//优化public void floyd1() {int len = 0;//保存距离//对中间顶点遍历，k就是中间顶点的下标[A,B, C,D, E, F, G]for(int k=0;k<dis.length;k++) {//从i顶点开始出发[A,B,C,D,E, F, G]for(int i=0;i<dis.length;i++) {if(dis[k][i]!=FloydDemo.max&&dis[k][i]!=0) {for(int j=i+1;j<dis.length;j++) {if(dis[k][j]!=0&&dis[k][j]!=FloydDemo.max) {len = dis[i][k]+dis[k][j];if(len<dis[i][j]) {dis[i][j]=dis[j][i]=len;pre[i][j]=pre[j][i]=pre[k][j];}}}}}}}
}

package com.xhl.Floyd;public class FloydDemo {public static final int max = 10000;public static void main(String[] args) {char[] vertex = new char[] {'A','B','C','D','E','F','G'};//邻接矩阵表示int[][] weight = new int[][] {{0,5,7,max,max,max,2},{5,0,max,9,max,max,3},{7,max,0,max,8,max,max},{max,9,max,0,max,4,max},{max,max,8,max,0,5,4},{max,max,max,4,5,0,6},{2,3,max,max,4,6,0}};Graph g = new Graph(vertex, weight, vertex.length);g.floyd1();g.show();}}

10、马踏棋盘算法

马踏棋盘算法介绍和游戏演示

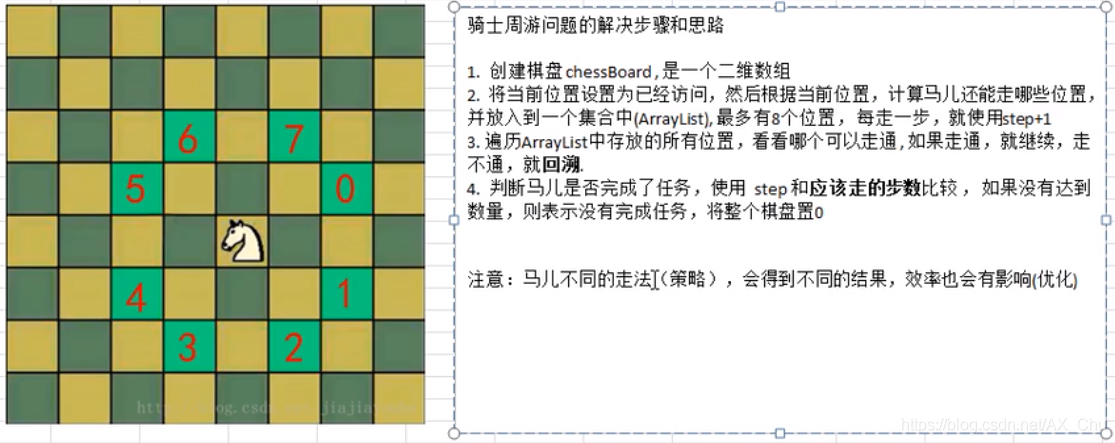
1. 马踏棋盘算法也被称为骑士周游问题
2. 将马随机放在国际象棋的8X 8棋盘Board[0~ 7][0~7]的某个方格中，马按走棋规则(马走日字)进行移动。要求每个方格只进入一次，走遍棋盘上全部64个方格
   

马踏棋盘游戏代码实现

1. 马踏棋盘问题(骑士周游问题)实际上是图的深度优先搜索(DFS)的应用。.
2. 如果使用回溯(就是深度优先搜索)来解决，假如马儿踏了53个点，如图:走到了第53个，坐标(1,0)，发现已经走到尽头，没办法，那就只能回退了，查看其他的路径，就在棋盘上不停的回溯…，思路分析+代码实现
   ➢对第一种实现方式的思路图解.
   
3. 分析第一种方式的问题，并使用贪心算法(greedyalgorithm) 进行优化。解决马踏棋盘问题.
   

package com.xhl.composite;import java.awt.Point;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;public class HorseChessboard {private static int X=8;//列private static int Y=8;//行private static boolean visited[];//标记各个位置是否被访问过private static boolean finished;//是否所以位置都被访问private static int[][] chessboard = new int[X][Y];public static void main(String[] args) {int row = 5;int column = 5;//初始行列visited = new boolean[X*Y];traversalChessboard(row-1, column-1, 1);for(int[] rows:chessboard) {System.out.println(Arrays.toString(rows));}}//* @param row马儿当前的位置的行从0开始//* @param column马儿当前的位置的列从0开始//* @param step 是第几步,初始位置就是第1步public static void traversalChessboard(int row,int column,int step) {chessboard[row][column]=step;visited[row*X+column]=true;//获取当前位置可以走的下一个位置的集合ArrayList<Point> ps = next(new Point(row,column));//对ps进行排序,排序的规则就是对ps的所有的Point对象的下一步的位置的数目，进行非递减排序sort(ps);while(!ps.isEmpty()) {Point p = ps.remove(0);if(!visited[p.y+p.x*X]) {traversalChessboard(p.x, p.y, step+1);}}//判断马儿是否完成了任务，使用step和应该走的步数比较//如果没有达到数量，则表示没有完成任务，将整个棋盘置0//说明:step<X*Y成立的情 况有两种//1.棋盘到目前位置，仍然没有走完//2.棋盘处于一个回溯过程if(step<X*Y&&!finished) {chessboard[row][column] = 0;visited[row*X+column]=false;}else {finished = true;}}private static void sort(ArrayList<Point> ps) {ps.sort(new Comparator<Point>() {@Overridepublic int compare(Point arg0, Point arg1) {int count0 = next(arg0).size();int count1 = next(arg1).size();return count0-count1;}});}public static ArrayList<Point> next(Point point) {ArrayList<Point> ps = new ArrayList();Point p = new Point();if((p.x=point.x-2)>=0&&(p.y=point.y-1)>=0) {ps.add(new Point(p));}if((p.x=point.x-1)>=0&&(p.y=point.y-2)>=0) {ps.add(new Point(p));}if((p.x=point.x-2)>=0&&(p.y=point.y+1)<Y) {ps.add(new Point(p));}if((p.x=point.x-1)>=0&&(p.y=point.y+2)<Y) {ps.add(new Point(p));}if((p.x=point.x+1)<Y&&(p.y=point.y-2)>=0) {ps.add(new Point(p));}if((p.x=point.x+2)<Y&&(p.y=point.y-1)>=0) {ps.add(new Point(p));}if((p.x=point.x+1)<Y&&(p.y=point.y+2)<Y) {ps.add(new Point(p));}if((p.x=point.x+2)<Y&&(p.y=point.y+1)<Y) {ps.add(new Point(p));}return ps;}}