练习:
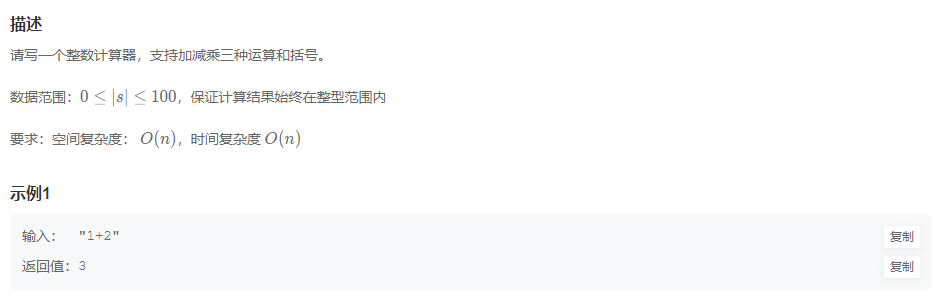
题目描述：
学校有一个在线学习系统，没门课程由N个页面组成（0< N<= 10000）个页面组成，学生从第一页开始按顺序学到最后一页提交学习记录。
系统会记录每页停留的时间（单位秒），当学生提交时会分析时间是否满足要求，分析规则如下：
每分钟（60秒）之内学完的页面不能大于4页。
例如系统记录到某学生页面停留时间如下：
10 120 10 20 10 10 50
该学生第一分钟学完1页，第二分钟学完0页，第三分钟学完5页，第四分钟学完1页，则判定为不满足要求。
输入描述：

输入数据包含多个学生的提交记录，第一行是整数表示记录个数，每个记录占一行，每行的第一个数是N，表示页面数，然后是每个页面的学习时间。

输出描述：

对于每组输入数据，满足输出1，不满足输出0，每组输出占一行。

输入

5
2 10 10
4 10 15 20 30
5 10 10 10 10 10
6 10 20 20 70 10 10
8 10 120 10 10 10 10 10 10

输出

1
1
0
1
0

---

思路：统计每一分钟，翻过的页数，超过60秒时，将时间与60取模，且页数归0，小于60就累加页数，大于4就返回0，否则返回1

#include <bits/stdc++.h>
using namespace std;
bool judge(vector<int> a) {int sum = 0, page = 0;for(int x : a) {sum += x;if(sum > 60) {sum %= 60;page = 0;}page++;if(page > 4) return 0;}return 1;
}
int main() {int t;cin >> t;while(t--) {int n, sum = 0, page = 0;vector<int> a;cin >>n;for(int i = 0; i < n; i++) {int x;cin >>x;a.push_back(x);}cout << judge(a) <<endl;}return 0;
}

2021华为秋招笔试题-软件 9.09 参考
1.完美序列

示例1：

输入：
3 2 1 1 2 3
输出：
1
说明：前三个玩具形成“完美序列”。

示例2：

输入：
3
1 2 3
3 2 1
6
1 2 1 2 3 3
5 4 3 2 1 1
输出：
1

#

2.最长的水沟

最长的水沟
#include <iostream>
#include <algorithm>using namespace std;const int N = 1e3 + 10;
int n, m;
int graph[N][N];
int flag[N][N];
int path[N][N];int dx[] = { -1, 0, 0, 1 };
int dy[] = { 0, 1, -1, 0 };int dfs(int x, int y) {if (path[x][y] > 1) return path[x][y];int bf = path[x][y];for (int k = 0; k < 4; ++k) {int nx = x + dx[k], ny = y + dy[k];if (nx >= 0 && nx < n && ny >= 0 && ny < m && flag[nx][ny] == 0 && graph[x][y] > graph[nx][ny]) {flag[nx][ny] = 1;path[x][y] = max(path[x][y], bf + dfs(nx, ny));flag[nx][ny] = 0;}}return path[x][y];
}int main() {cin >> n >> m;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {cin >> graph[i][j];flag[i][j] = 0;path[i][j] = 1;}}int ans = 1;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {flag[i][j] = 1;ans = max(ans, dfs(i, j));flag[i][j] = 0;}}cout << ans << endl;return 0;
}

3.最大异或和

最大异或路径
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<string>
using namespace std;
int name[100005], weight[100005], l[100005], r[100005];
int ans;
void dfs(int p, int now){now ^= weight[p];ans = max(now, ans);if (l[p] > 0){dfs(l[p], now);}if (r[p] > 0){dfs(r[p], now);}
}
void solve(){int n;cin >> n;for (int i = 1; i <= n; i++){int x;cin >> x;cin >> weight[x] >> l[x] >> r[x];}ans = 0;for (int i = 1; i <= n; i++){dfs(i, 0);}cout << ans << endl;
}
int main(){solve();return 0;
}