目录

2021华为笔试第一道

缓存转发数据包统计（100%）

解题思路：

参考代码：

2021华为笔试第二题

查找知识图谱中的实例知识（100%）

解题思路：

参考代码：

2021华为笔试第三题

湖泊连通（100%）

解题思路：

参考代码： 

---

2021华为笔试第一道

缓存转发数据包统计（100%）

题目描述

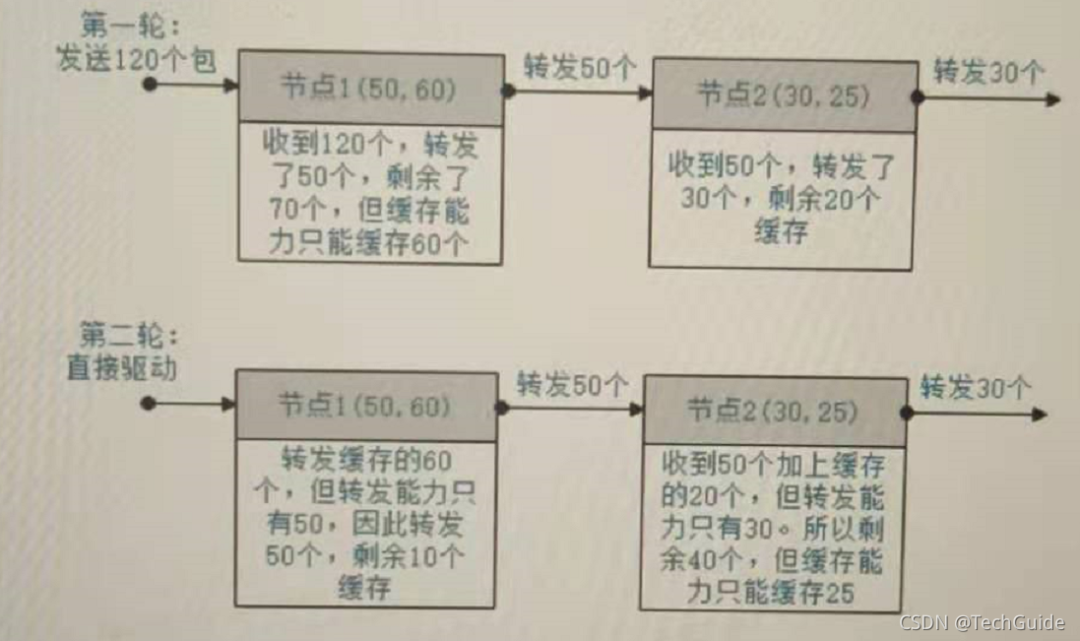
有k个节点的转发队列，每个节点转发能力为m，缓存能力n(表示此节点可立即转发m个包，剩余的缓存，最多缓存n个包，再剩余的丢弃，缓存的包在下一轮继续转发)。另外，此队列中某些节点可能因故障需要直接跳过转发，但不会有两个连续故障的节点。现分两轮操作，第一轮向此队列发送a个数据包让其转发;第二轮，直接驱动让缓存的数据包继续转发。

求两轮最后可能收到的最少数据包总个数(如果第二轮缓存仍有数据包缓存包按丢弃处理) 1 <= k <= 40 1 <= m,n <= 1000 1 <= a <= 1000

例如:有两个节点，节点1(转发能力m:50，缓存能力n:60) 和节点2(m:30，n:25)，发送包数为120。

在没有节点故障时:

输入描述：第一行队列长度k 第二行为k个节点转发能力数组，以空格分隔。m,n以逗号分隔，例如10,20 11,21 12,22 第三行数据包个数a

2
50,60 30,25
120

输出描述：

55 

解释:参见题目中的图例，当第一个节点故障时，仅第二个节点转发，此时收到的包最少。

解题思路：

双层动态规划。

1.首先是定义vector<vector<int>>cap(k+1, vector<int>(2))，保存每个节点的转发能力和缓存能力；(输入节点为第0个节点)

2.定义vector<vector<int>>dp(k+1, vector<int>(2))，保存每个节点第一次转发的数量和第二次转发的数量。(输入节点第一次转发数量为a，第二次转发数量为0)

3.计算(dpfun())每个节点第一次转发和第二次转发的数量send1和send2：

第一次转发的数量为从前一节点接收到的第一次转发的数量和该节点转发能力的最小值：

cur_cap[0]：为当前节点的转发能力，cur_cap[1]：当前节点的缓存能力，也就是dp_fun()传入的cap[i]。

pre[0]：上一节点第一次转发的数量，pre[1]：上一节点第二次转发的数量，也就是dp_fun()传入的cap[i]。

send1 = min(pre[0], cur_cap[0]);

第二次转发的数量需要分情况讨论，即第一次从上一节点转发来的是否全部被转走。不过最大转发数量也就是转发能力与缓存能力加上上一节点第二次转发数量的最小值。

send2 = min(pre[1] + cur_cap[1], cur_cap[0]);

如果上一节点第一次转发的数量大于当前节点的转发能力(有缓存的情况)，则当前节点第二次转发的数量为上一节点第二次转发的数量加上当前节点第一次的缓存：

send2 = min(pre[1] + pre[0] - cur_cap[0], send2);

否则，当前节点第二次转发的就是上一节点第二次转发的数量：

send2 = min(pre[1], send2);

4.再分析节点存在故障的情况，因为不会有连续两个节点故障，所以遍历所有节点，交叉转发，然后每一个节点转发情况取较小的一个。

vector<int> res1 = dpfun(dp[i - 1], cap[i]);//前一个节点没有故障
vector<int> res2 = dpfun(dp[i - 2], cap[i]);//前一个节点故障
dp[i] = res1[0] + res1[1] <= res2[0] + res2[1] ? res1 : res2;

5.输出最后一个节点，或倒数第二个节点转发数量中的较小值即可。

res = min(dp[k][0] + dp[k][1], dp[k - 1][0] + dp[k - 1][1]);

参考代码：

#include<bits/stdc++.h>
using namespace std;//根据前一个节点发送的数据包 和当前节点的能力
//计算当前节点发送的数据包
//pre:前一节点(两次)转发的数量  cur_cap：当前节点(转发能力，缓存能力)
vector<int> dpfun(vector<int> &pre, vector<int> &cur_cap) {int send1 = min(pre[0], cur_cap[0]);//第一次发送的数据包量int send2 = min(pre[1] + cur_cap[1], cur_cap[0]);//第二次发送的数据包数最大可能情况//判断第一次转发来的数据包是否已被转走if (pre[0] - cur_cap[0] > 0)//来的数据包大于当前节点的转发能力send2 = min(pre[1] + pre[0] - cur_cap[0], send2);elsesend2 = min(pre[1], send2);return vector<int> {send1, send2};
}
int main() {int k, a;//节点数k 发送包数aint res = 0;//两轮最少能转发的数据包vector<vector<int>> cap;//cap(k, vector<int>(2)) 节点能力数组 cap.push_back(vector<int>{0, 0});//头结点不需考虑能力cin >> k;int m1, n1;//m1转发能力 n1缓存能力char ch;for (int i = 0; i < k; i++) {cin >> m1 >> ch >> n1;cap.push_back(vector<int>{m1, n1});}cin >> a;vector<vector<int>> dp(k + 1, vector<int>(2));//第i个节点两次发送的数据包数dp[0][0] = a;//第0个节点第一次发送a个数据包dp[0][1] = 0;//第0个节点第二次发送0个数据包dp[1] = dpfun(dp[0], cap[1]);res = min(dp[0][0] + dp[0][1], dp[1][0] + dp[1][1]);//如果只有一个节点if (k == 0)cout << a << endl;else {for (int i = 2; i <= k; i++) {vector<int> res1 = dpfun(dp[i - 1], cap[i]);//前一个节点没有故障vector<int> res2 = dpfun(dp[i - 2], cap[i]);//前一个节点故障dp[i] = res1[0] + res1[1] <= res2[0] + res2[1] ? res1 : res2;}res = min(dp[k][0] + dp[k][1], dp[k - 1][0] + dp[k - 1][1]);cout << res << endl;}return 0;
}

2021华为笔试第二题

查找知识图谱中的实例知识（100%）

知识图谱是一种结构化的语义网络，用于描述物理世界中的概念及其实例的相关关系。可以把知识图谱看成是一种有向图，图中的点是概念或实例，图中的边是概念及其实例的相关关系。

现定义一种简单的知识图谱

概念：包括父概念及其子概念，通过subClassOf关系关联，父子概念可以有多个层级；实例:仅和概念之间通过instanceOf关系关联: 关系:以三元组的形式表示，三元组是一个以空格为成员间分隔符的字符串。例如"student subClassOf person"表示student是person的子概念，"apple instanceOf fruit"表示apple是概念fruit的实例。给定一个知识图谱，请编写一个方法，可以根据一个概念查找其所有的实例。如果一个概念拥有子概念，那么返回的结果需要包含其所有子概念的实例;如果输入的概念没有实例，则返回字符串"empty"(说明:输出字符串文本不需要包含引号)。

给定的图谱满足以下限制: 1、有向图中不存在环路 2、所有点和关系的定义对大小写敏感

输入描述：输入第1行，表示图谱中关系的数量n，取值范围[1,10000] 从第2行到n+1行，表示图谱中的关系，每一行是一个关系三元组第n+2行，表示待查找的元节点，是关系三元组中存在的点。每行字符的长度不超过100。

3
student subClassOf person 
Tom inslenceOf student 
Marry instanceOf person 
person

输出描述按字典序升序排列的字符串数组，其内容是概念及其子概念的所有实例。

Marry Tom 

解释:student是person的子概念，Tom是student的实例，Marry是person的 实例，Marry的字典序小于Tom，所以返回Marry Tom。

解题思路1：

根据instanceOf查找它的父节点是否为target。

1.不管是 subClassOf还是instancOf，左边的是子节点，右边的是父节点。

2.定义哈希集合hash_set(instance)存储instancOf的子节点(每一对的第一个输入)。

3.定义哈希映射unordered_map(hash)存储所有instanceOf和sunClassOf。

4.根据hash_set遍历其父节点是否能到达目标节点即可，若满足则存入到set中，默认字典排序。若不满足则一直向父关系寻找，直到该关系结束。

5.因为存储满足该实例的节点存在set中，是有序的。所以直接输出，无需排序。

也就是用一个map存储关系，用一个set存储instance。然后遍历每一个instance，如果其父节点，或者一直向父关系遍历，如果能找到与目标概念相等，则该实例满足要求，存在set里。

参考代码1：

#include <bits/stdc++.h>
using namespace std;int main(int argc,char* argv[]){int n;cin>>n;unordered_map<string,string> hash;//val是父节点unordered_set<string> instance;//存储instacnOfstring s1,s2,s3;for(int i=0;i<n;++i){cin>>s1>>s2>>s3;if(s2=="instanceOf")instance.insert(s1);hash[s1]=s3;}string ss;cin>>ss;set<string> ret;for(auto s:instance){string s1=s;while(hash.count(s1)){if(hash[s1]==ss){ret.insert(s);break;}s1=hash[s1];}}if(ret.size()==0){cout<<"empty"<<endl;}else{int i=0;for(auto s:ret){if(i==0) cout<<s;else cout<<" "<<s;++i;}}return 0;
}

解题思路2：

递归实现

1.定义两个map，分别存储instance，subClass。

    map<string, vector<string>> subClass;//存储subClassOf关系 可能会一对多
    map<string, vector<string>> instance;//存储instanceOf关系 可能会一对多

2.从子节点递归向上找

参考代码2：

#include<bits/stdc++.h>
using namespace std;void solve(map<string, vector<string>> &subClass, map<string, vector<string>> &instance, vector<string> &res, string &target) {for (string str : instance[target])res.push_back(str);for (string str : subClass[target])solve(subClass, instance, res, str);return;
}
int main() {int n;cin >> n;map<string, vector<string>> subClass;//存储subClassOf关系 可能会一对多map<string, vector<string>> instance;//存储instanceOf关系 可能会一对多for (int i = 0; i < n; i++) {string head;cin >> head;string relation;cin >> relation;string tail;cin >> tail;if (relation == "subClassOf")subClass[tail].push_back(head);elseinstance[tail].push_back(head);}string target;cin >> target;vector<string> res;solve(subClass, instance, res, target);sort(res.begin(), res.end());if (res.empty())cout << "empty";else {for (string str : res)cout << str << " ";}cout << endl;return 0;
}

2021华为笔试第三题

湖泊连通（100%）

题目描述

地图上有多个湖泊，为增强湖泊的抗暴雨能力，需要在湖泊间挖出通道使得湖泊之间能够连通(对角线视为不连通)。有的陆地是坚硬的石头，挖通需要耗费的精力是普通陆地的2倍，即一个普通格子的长度为1，一个有坚硬石头的格子的长度为2。地图用二维矩阵表示，每个位置只有三种可能，0为湖泊，1为普通陆地，2为坚硬的石头，地图最大为MN。需要返回挖通所有湖泊的最短通道，如果通道不存在的话，返回0 限制:M、N最大为20,湖泊个数不超过11。

输入描述：第一行为M 第二行为N 第三行开始为M*N的地图矩阵

5 
4
0 1 1 0
0 1 0 0
0 1 0 0
0 1 0 1
1 1 1 1

输出描述：返回挖通所有湖泊的最短通道

1

解释:地图上共有2片湖泊，只需要挖通1块陆地，2片湖泊即可连通。

解题思路：

这道题是【斯坦纳树】的经典例题。斯坦纳树是这样一类问题：带边权无向图上有几个（一般约10个）点是【关键点】，要求选择一些边使这些点在同一个联通块内，同时要求所选的边的边权和最小。

怎么解决斯坦纳树问题？……其实，就是一种状压DP。

dp[i][j]表示以i号节点为根，当前状态为j（j的二进制中已经与i连通的点对应位置为1）。

这个“以i为根”是哪来的呢？其实i可以是联通块中任意一个点，没有额外限制，只是引入这个i就可以DP了。

当根i不改变时（即合并两个都包含i的联通块）状态转移方程是：

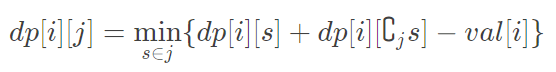
参考代码： 

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <queue>
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){char c;bool op = 0;while(c = getchar(), c < '0' || c > '9')if(c == '-') op = 1;x = c - '0';while(c = getchar(), c >= '0' && c <= '9')x = x * 10 + c - '0';if(op) x = -x;
}
template <class T>
void write(T x){if(x < 0) putchar('-'), x = -x;if(x >= 10) write(x / 10);putchar('0' + x % 10);
}const int INF = 0x3f3f3f3f;
int n, m, K, root, f[101][1111], a[101], ans[11][11];
bool inq[101];
typedef pair<int, int> par;
typedef pair<par, int> rec;
#define fi first
#define se second
#define mp make_pair
#define num(u) (u.fi * m + u.se)
rec pre[101][1111];
const int dx[] = {0, 0, -1, 1};
const int dy[] = {1, -1, 0, 0};
queue<par> que;bool legal(par u){return u.fi >= 0 && u.se >= 0 && u.fi < n && u.se < m;
}
void spfa(int now){while(!que.empty()){par u = que.front();que.pop();inq[num(u)] = 0;for(int d = 0; d < 4; d++){par v = mp(u.fi + dx[d], u.se + dy[d]);int nu = num(u), nv = num(v);if(legal(v) && f[nv][now] > f[nu][now] + a[nv]){f[nv][now] = f[nu][now] + a[nv];if(!inq[nv]) inq[nv] = 1, que.push(v);pre[nv][now] = mp(u, now);}}}
}
void dfs(par u, int now){if(!pre[num(u)][now].se) return;ans[u.fi][u.se] = 1;int nu = num(u);if(pre[nu][now].fi == u) dfs(u, now ^ pre[nu][now].se);dfs(pre[nu][now].fi, pre[nu][now].se);
}int main(){read(n), read(m);memset(f, 0x3f, sizeof(f));for(int i = 0, tot = 0; i < n; i++)for(int j = 0; j < m; j++){read(a[tot]);if(!a[tot]) f[tot][1 << (K++)] = 0, root = tot;tot++;}for(int now = 1; now < (1 << K); now++){for(int i = 0; i < n * m; i++){for(int s = now & (now - 1); s; s = now & (s - 1))if(f[i][now] > f[i][s] + f[i][now ^ s] - a[i]){f[i][now] = f[i][s] + f[i][now ^ s] - a[i];pre[i][now] = mp(mp(i / m, i % m), s);}if(f[i][now] < INF)que.push(mp(i / m, i % m)), inq[i] = 1;}spfa(now);}write(f[root][(1 << K) - 1]), enter;dfs(mp(root / m, root % m), (1 << K) - 1);for(int i = 0, tot = 0; i < n; i++){for(int j = 0; j < m; j++)if(!a[tot++]) putchar('x');else putchar(ans[i][j] ? 'o' : '_');enter;}return 0;
}