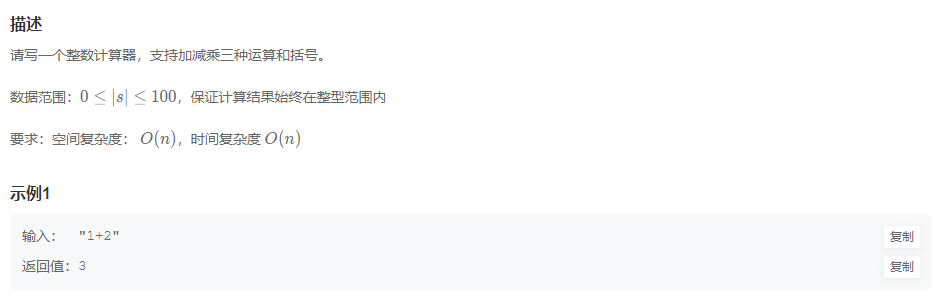
1、猪场防疫
老李在多年前承包了一个养猪场, 并引入了若干只种猪,经过这些年的经营,现在养猪场有N只猪,编号从0到N-1 (每只猪无论生死都有唯一的编号) ;
老李在每只猪生产的时候记下了生产的母猪和出生的小猪,格式: x y1 y2 …(注: x为猪妈妈,y1、 y2、 …为新生的猪崽,以上编码均在0…N-1内,每只猪可以多次生产,每个猪崽只有一个猪妈妈) ;
为了防疫需要,要检查任意两只猪是否有亲戚关系(两只猪具有相同的祖先),并计算出关系亲疏情况(关系距离,相同编号距离为0)。
输入
第一行猪总数N
第二行记录数M
后续M行记录,空格分割
x y1 y2 …
…
最后一行 两个编号 m1 和m2 表示待检查的两只猪的编号
思路: 这题一看就差不多能想到并查集,如果不是求距离而是求是否有亲戚关系(有共同祖先),那就是标准的并查集模板,但是加了求距离,并查集就不是很好做。所以我们呢换个思路
我们可以简单的想象出来 m1 一直往上溯源,是形成一条链是吧(类似高中生物的遗传图谱),那就意味着每个个体溯源到最初祖先 都是一条链表。换句话说,题目就是让我们求两条链表中相同数字出现的最早位置(就是最近公共祖先了),但是由于我用python写嘛,所以用数组,直接用index函数求下标了,所以用了数组来模拟。同时我俩简化判断一个属在不在另一条链中(数组),所以用到了set 加快速度
n = int(input())
m = int(input())
num_dict = dict()
for i in range(m): # 构建每只猪的父节点 dict ,处理输入arr = list(map(int,input().split(" ")))for i in range(1,len(arr)):num_dict[arr[i]] = arr[0]m1,m2 = list(map(int,input().split(" ")))# 构建两个数组(其实就是两条链辣)
arr1 = [m1]
while m1 in num_dict.keys():arr1.append(num_dict[m1])m1 = num_dict[m1]arr2 = [m2]
while m2 in num_dict.keys():arr2.append(num_dict[m2])m2 = num_dict[m2]set1 = set(arr1) # 便于后续检查
ans = -1
for i in range(len(arr2)):if arr2[i] not in set1: # 判断当前编号是否也在arr1中出现了continueelse:ans = i + arr1.index(arr2[i])break
print(ans)
测试用例1
输入 :
3
1
0 1 2
0 1
输出:
1
解释:0-1 是亲戚关系,距离是1
测试用例1
输入 :
5
2
0 1 2
1 3 4
2 4
输出:
3
解释:2-0-1-4 是亲戚关系,距离是3
2、速战速决
在一个MxN的街区中,有一个士兵S和一个敌人E, 标识X为无法通过的街区,标识B为可以通过的街区;士兵在一个单位时间内可以从一个街区移动到相邻的街区(土兵每次只能水平或者垂直方向移动一个街区) ;士兵每次改变方向时,需要额外花费个 单位的时间(士兵第一次移动个街区的时候,不用考虑其初始方向,即只需要一个单位时间即可到达相邻街区)。计算士兵S最少需要多少时间才能到达E所在的街区。
输入
第一行为两个数字,表示街区的大小,M行,N列; (1 <= M.N<=1000,M、N不同时为1)
接下来M行,每行N个字母,字母S表示士兵所在街区,字母E表示敌人所在街区,字母X表示障碍,字母B表示可以经过的街区。(只有1个S,一个E)
输出
最少需要的时间,当士兵S永远无法到达敌人E所在的街区时,输出-1
思路:其实很简单 就是二维数组两点最短路径 一般用bfs最好,但是由于题目加了限制,换向时要罚一单位时间,所以只能用dfs,记录一个方向信息即可,方向信息也简单,在dfs中一般有一个数组来充当上下左右嘛。数组下标和方向时一一对应的,所以直接使用来判断就行
m,n = list(map(int,input().split(" ")))
arr = []
startx,starty,endx,endy = -1,-1,-1,-1
for i in range(m):temp = list(input())arr.append(temp)if "S" in temp:startx = istarty = temp.index("S")if "E" in temp:endx = iendy = temp.index("E")class solution2:def help(self,arr,startx,starty,endx,endy,m,n):if startx == -1 or endx == -1 or starty==-1 or endy ==-1:return -1self.ans = 999999self.visit = set()self.arr = arrself.endx= endxself.endy = endyself.m = mself.n = nself.DFS(startx, starty, -1, -1)def DFS(self,x, y, length, direction):if x == self.endx and y == self.endy:self.ans = min(length,self.ans)print(length,self.ans)returnself.visit.add((x, y)) # 这个点探索过了nextarr = [[0, 1], [0, -1], [-1, 0], [1, 0]] # 上下左右for i in range(4):tx = x + nextarr[i][0]ty = y + nextarr[i][1]if tx < 0 or ty < 0 or tx >= self.m or ty >= self.n:continueif self.arr[tx][ty] == "X" or (tx, ty) in self.visit:continueself.DFS(tx, ty, length + 1 + int(i != direction), i)solu = solution2()
solu.help(arr,startx,starty,endx,endy,m,n)
if 999999==solu.ans:print(-1)
else:print(solu.ans)
测试用例