三道题

总结：写的时候太紧张了，很烦

T1

题目：给出n个任务的最晚完成时间（单位为小时）和对应积分，每小时只能做一个任务，且超时后不获得积分，求出最大的价值和。

解法：排序+堆
先对数组排序，先对最晚完成时间升序排序，再对积分降序排序。
用小根堆存储已经完成的任务的积分，遍历所有任务，当该任务未超时时加入堆，如果超时，比较两个任务的积分，将积分更多的任务加入堆，并且pop。
最后堆里面的就是能拿到积分的任务。

#include <bits/stdc++.h>using namespace std;using ll = long long;int main() {int n;cin >> n;vector<pair<ll, ll>> v;for (int i = 0; i < n; ++i) {int t1, t2;cin >> t1 >> t2;v.push_back({ t1, t2 });}sort(v.begin(), v.end(), [&](const auto& lhs, const auto& rhs) {return lhs.first != rhs.first ? lhs.first < rhs.first : lhs.second > rhs.second;});priority_queue<ll, vector<ll>, greater<ll>> pq;for (const auto& i : v) {if (i.first > pq.size()) pq.push(i.second);else {if (i.second > pq.top()) {pq.pop();pq.push(i.second);}}}ll res = 0;while (!pq.empty()) {res += pq.top();pq.pop();}cout << res << endl;return 0;
}
// T1
/*
7
1 6
1 7
3 2
3 1
2 4
2 5
6 115
*/

T2

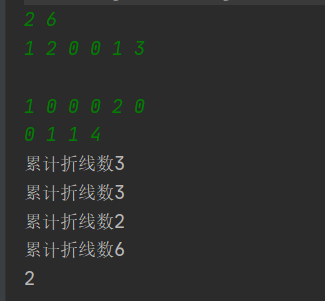
题目：给出n个节点，m条边的带权有向图，给出一个起点s，问是否能访问到所有点，能的话输出最长路径。
解法：dfs

只有图片，懒得打一遍了

T3

题目：给定一个棋盘，出发点和目的地，棋盘上有若干障碍，问棋子”马“最少需要多少步才能到达目的地。

解法：bfs

#include <bits/stdc++.h>using namespace std;using ll = long long;int main() {int w, h;cin >> w >> h;vector<string> v;string tmp;int start_i, start_j;int des_i, des_j;// INPUTfor (int i = 0; i < w; ++i) {cin >> tmp;v.push_back(tmp);int pos1 = tmp.find("H");if (pos1 != -1) {start_i = i;start_j = pos1;}int pos2 = tmp.find("T");if (pos2 != -1) {des_i = i;des_j = pos2;}}// INITvector<vector<int>> visit(w, vector<int>(h, 0));const vector<pair<int, int>> neighbor{ {-1, 0}, {0, 1}, {1, 0}, {0, -1} };const vector<vector<pair<int, int>>> direction{ {{-2,  1}, {-2, -1}},{{-1,  2}, {1 ,  2}},{{2 ,  1}, {2 , -1}},{{-1, -2}, {1 , -2}} };queue<pair<int, int>> q;q.push({ start_i, start_j });int res = 0;// BFSwhile (!q.empty()) {int len = q.size();for (int i = 0; i < len; ++i) {auto p = q.front(); q.pop();visit[p.first][p.second] = 1;if (p.first == des_i && p.second == des_j) {cout << res << endl;return 0;}for (int j = 0; j < 4; ++j) {int nei_i = p.first + neighbor[j].first, nei_j = p.second + neighbor[j].second;if (nei_i >= 0 && nei_i < w && nei_j >= 0 && nei_j < h && v[nei_i][nei_j] != '#') { // neighbor validfor (int k = 0; k < 2; ++k) {int newi = p.first + direction[j][k].first;int newj = p.second + direction[j][k].second;if (newi >= 0 && newi < w && newj >= 0 && newj < h && !visit[newi][newj]) {q.push({ newi, newj });}}}}}++res;}cout << "-1" << endl;return 0;
}
// T3
/*
5 13
........H...#
........#....
.....#.......
.#...........
..........T#.
4
5 13
........H...#
........#....
.....#.T.....
.#...........
...........#.
3
*/