等比数列求和

article/2025/9/17 14:55:51

引入：

先来看一个问题，求 $a^{b}$ 的所有约数之和 $mod$ $9901$ ；

解决思路如下：首先将 $a$ 分解质因数，表示为 $p_1^{c_1}\cdot p_2^{c_2}\cdot...\cdot p_{n}^{c_n}$ ，其中 $p_{i}\left ( 1\leqslant i\leqslant n \right )$ 均为质数，因此 $a^{b}$ 表示为： $p_1^{b\cdot c_1}\cdot p_2^{b\cdot c_2}\cdot...\cdot p_{n}^{b\cdot c_n}$ 。此时我们将 $a^{b}$ 的所有约数表示为集合 $\left \{ p_1^{k_1}\cdot p_2^{k_2} ...\cdot p_{n}^{k_{n}}\right \}$ ，从这 $n$ 个约数中选出 $i$ 个数的乘积即为一个约数。

此时我们根据乘法分配律反推：所有约数之和为： $\left ( 1+p_1+p_1^{2}+...+p_1^{b \cdot c_1} \right ) \cdot \left (1+p_2+p_2^{2}+...+p_2^{b \cdot c_2} \right ) \cdot ... \cdot \left ( 1+p_n+p_n^{2}+...+p_n^{b \cdot c_n} \right )$

而如何求解每一对括号内的等比数列和？

正文

等比数列求和通项公式：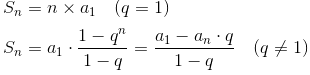

注意，如果解决此类问题，对于除法应为在 $mod\left ( p \right )$ 的条件下做同余，需要用到逆元，还需要关注 $p$ 是否为素数

而这里问题来了，我们想用更快的没有除法的方法求等比数列和 $sum(p,c)=\left ( 1+p+p^{2}+...+p^{c} \right )$

考虑分治法：如果 $c$ 为奇数， $sum(p,c)=\left ( 1+p+p^{2}+...+p^{\frac{c-1}{2}} \right )+\left ( p^{\frac{c+1}{2}}+...+p^{c} \right )$ $=\left ( 1+p+p^{2}+...+p^{\frac{c-1}{2}} \right )+p^{\frac{c+1}{2}} \cdot \left ( 1+p+p^{2}+...+p^{\frac{c-1}{2}} \right )$ $=(1+p^{ \frac {c+1} {2} }) \cdot sum(p, \frac{c-1}{2} )$

若 $c$ 为偶数：有类似地： $sum(p,c)=(1+p^{ \frac {c} {2} }) \cdot sum(p, \frac{c}{2} -1)+p^{c}$

具体代码实现：

ll sum(ll a,ll b,ll mod)
{if(b==0) return 1;if(b&1) return (sum(a,b/2,mod)*(quick_pow(a,b/2+1,mod)+1))%mod;else return ((sum(a,b/2-1,mod)*(quick_pow(a,b/2,mod)+1))+quick_pow(a,b,mod))%mod;
}

结合快速幂，可在 $Olog(c)$ 复杂度内求出等比数列和。