二叉树遍历
二叉树有三种遍历方法:前序(跟左右)跟节点在前面、中序(左跟右)跟节点在中间、后续(左右跟)跟节点在后面

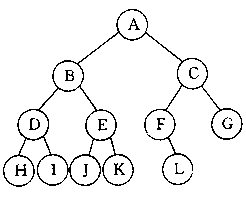
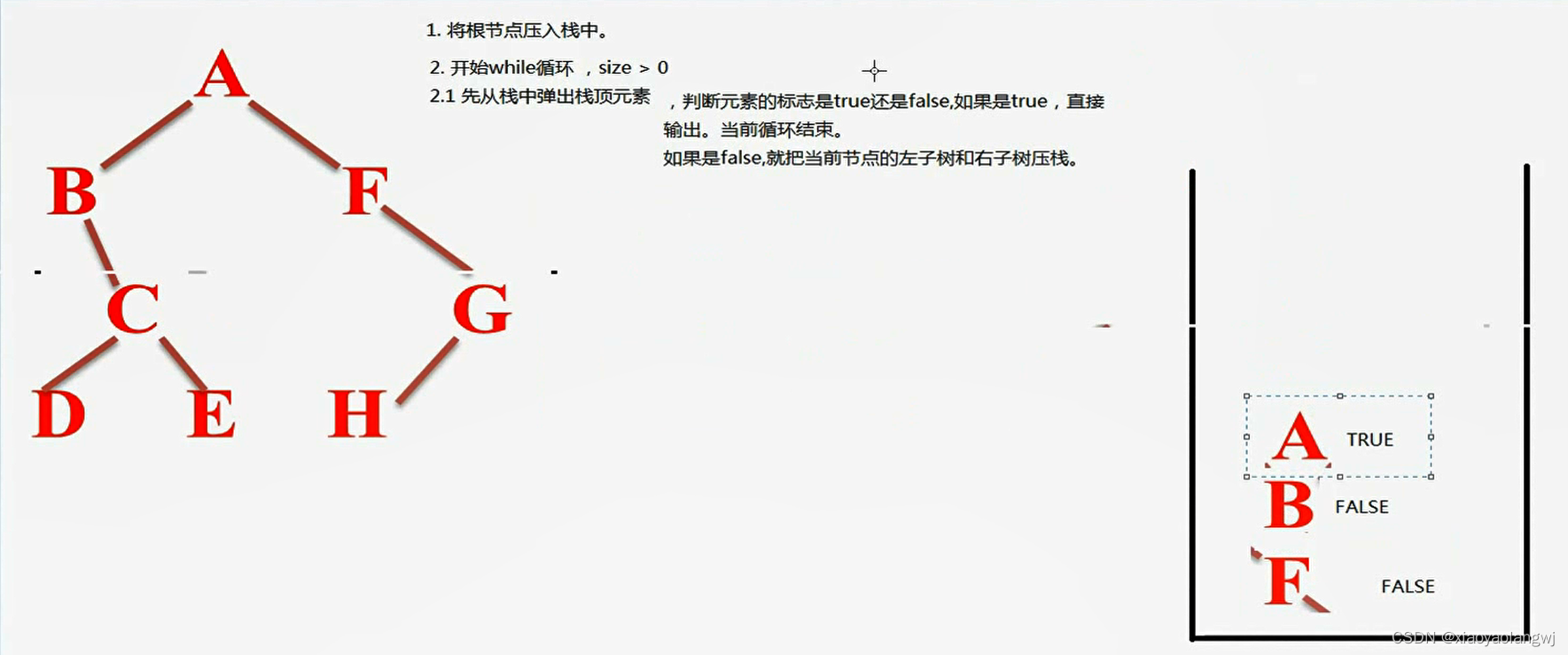
前序(跟左右):上图的二叉树,第一次跟左右对应ABC,对于B来说跟左右对应BD空, 汇总下顺序为:ABDC
如何通过计算机自动找出来呢?

我们实现的方法是通过栈来实现的,栈的特点是先进后出。

如果放入循序是A->B->C,出来的的是C->B->A 。如果希望出来的是A->B->C,则放入的顺序应该是C->B->A 。其中C对应上图树中的右,B对应于树中的左,A对应于树中的跟.
所以我们要按照右左跟的顺序往栈里面放数据,才能拿出来跟左右的前序遍历结果。

如何通过代码来实现
- new 一个
栈,栈是空的,我们首先把跟节点A放进去,目的是要变成放入顺序为C->B->A的栈。

先在的问题变成了,如何从只有跟节点A的栈变成放入顺序为C->B->A的栈。
- 首先
popA,然后把C放进去。 其中C=A->right,跟节点A比较有价值,他知道两个元素的地址。 - 然后把
A-right放进去,然后把A->left放进去,然后再把A放进去。此时A已经没有利用价值了,通过标记NULL将节点A杀掉。

- 如何
杀呢?先把nullpop掉,找到要卸磨杀驴的驴A,将它也pop掉。pop之后将A放在一个vector容器中。然后就变成了C->B

此时B没有NULL的标识,没有要杀的标签,所以说明这头驴B还有价值,那我们就需要利用它的价值,它的价值是左右两个节点的地址, - 在根据之前
A的流程,把B先pop出去,要获得B的跟左右的输出,就需要按照右左跟的顺序压栈。这里右是空,右就不用管了。B的左是D,因此将D压如栈中,然后跟上B本身。

- 此时
B就没有价值了,因为已经利用到了B它的左右子节点,因此B就是需要杀掉的驴,给B赋一个NULL,然后把NULLpop掉,把Bpop掉。紧接着把B放入vector容器中。 栈就剩下C和D了,此时Top不是NULL,说明D不是要杀掉的驴,它还存在使用价值,然后重复之前步骤,根据右左跟的顺序,D的右子节点为空因此不用写,D的左子节点也是空,不用写。此时D也就没有价值了,因为它的左右子节点都被找到并利用了。此时D就变成要杀掉的驴(比喻:卸磨杀驴,榨干玩剩余价值),将D赋予NULL,然后把NULLpop 出来,然后把Dpop出来,紧接着把D放入vector容器中。- 同理
C跟D一样,最后C也被放入了vector容器中 - 最后vector中的顺序为
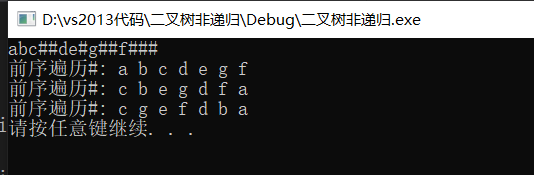
A->B->D->C,和我们之前自己算出来是一样的
代码
假设二叉树已经创建好了,需要有一个栈来实现,写一个函数来实现二叉树遍历。
定义树的节点.
typedef struct node
{int val;struct node* left; // 左子节点struct node* right; // 右子节点
}Treenode
定义函数void DieDai(Treenode* root) 形参为跟节点
先类似伪代码实现
vector<int> DieDai(Treenode* root)
{stack<Treenode*> stk;vector<int> v1;if(root!=NULL) stk.push(root);while(stk.empty==false){Treenode* top=stk.top;if(stk.top!=NULL) //不杀驴,利用其价值,可以找到左右子节点{stk.push(top->right);stk.push(top->left);stk.push(top);stk.push(NULL); //top的价值使用完了,需要贴上NULL标签}else{//stk.top=NULL 说明价值被利用干,需要卸磨杀驴stk.pop() //移除NULLtop=stk.top() //移除了NULL之后的,top对应的元素stk.pop() v1.push_back(top.val) }}return v1
}
总结
- 判断
top是否为NULL - 不是
NULL,按顺序右左跟 - 如果是
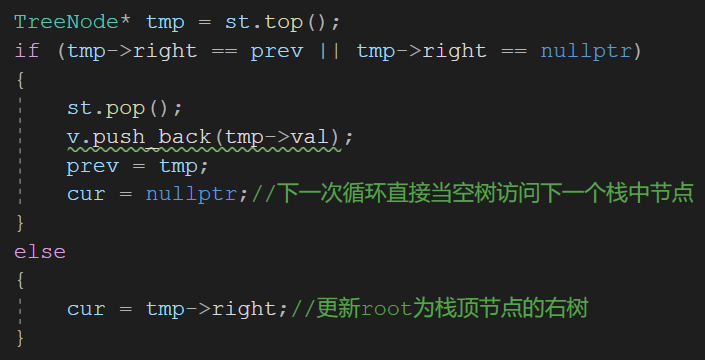
NULL,说明是要杀的驴:1. 将NULL(top)pop 掉 2.将新的top(栈元素)pop3. 将top中的val放到vector容器中
这就是完整的二叉树非递归遍历的顺序。