二叉树非递归遍历算法分析

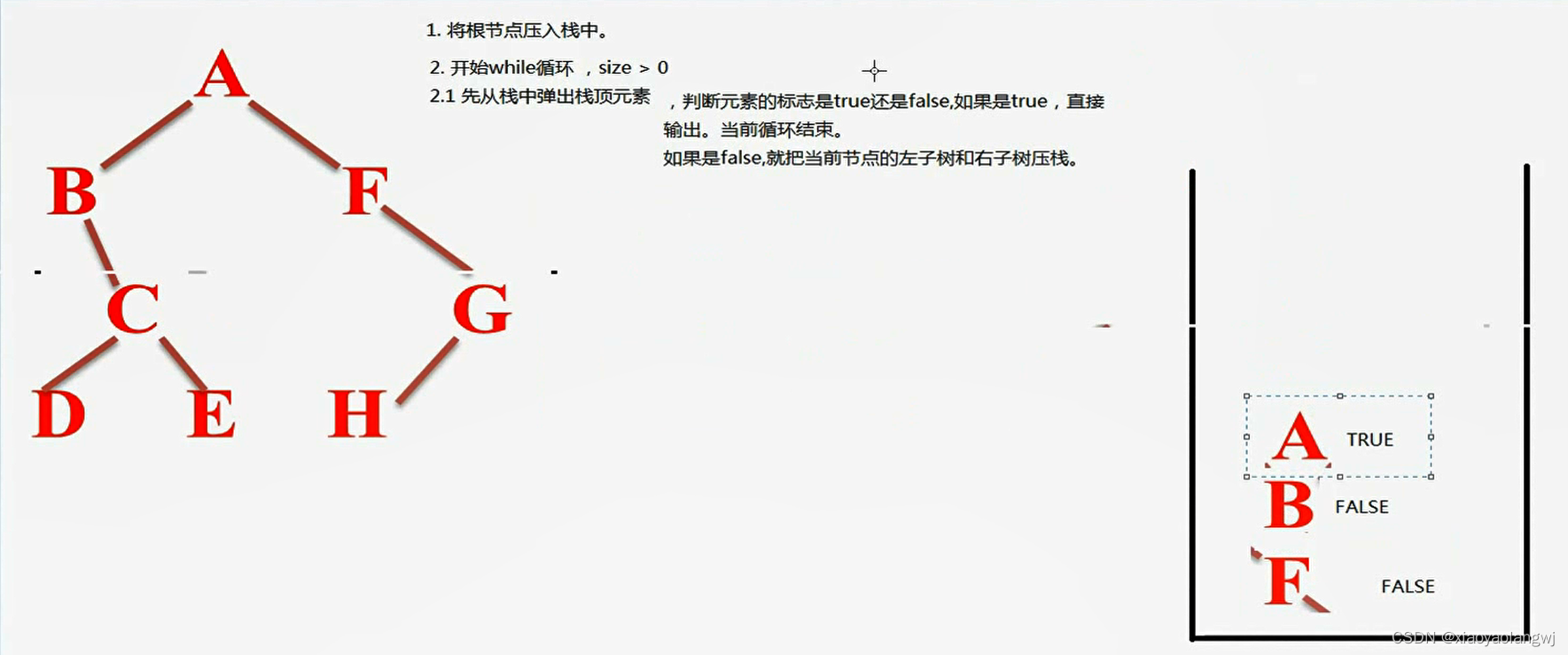
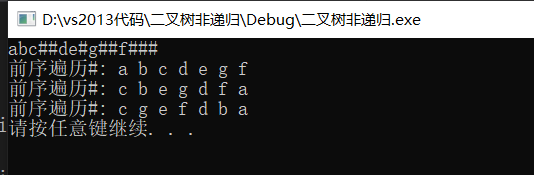
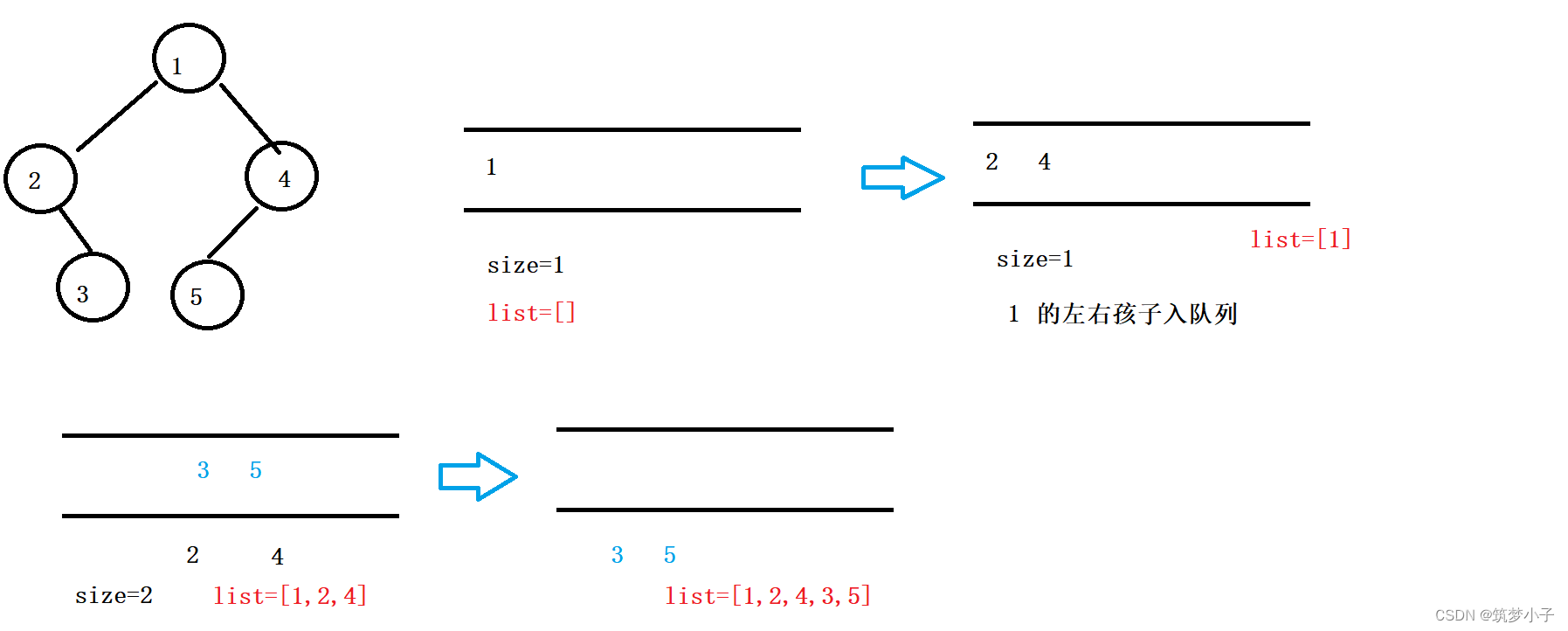
　　以前没有学习过树的相关算法，只是了解一些皮毛，最近开始认真学习它。看视频或者网上查资料，可以知道怎么去遍历一棵树，但是算法为什么是这样的呢？少有讲到。如果有一天，我忘记了这个算法，我需要重新去看视频，看文档，这不是我想要的。我想要的是，知道这个算法是怎么设计出来的。下次我忘记的时候，我需要一支笔，一张纸，重新设计出这个算法，而不是去找资料看视频。我想要知道的是，为什么如此，而不是仅仅知道如此而已。

一、三种遍历顺序

　　怎么记住三种遍历顺序：前序、中序、后序；前、中、后指的是什么。一棵树是怎么发展起来的：me，my->left_child，my->right_child，这是最基本的关系，me是中心，left和right跟me建立了一种联系，left和right再各自发展自己的child，于是一棵树就越来越庞大了。遍历过程，就是要把所有节点走一遍，而最基本的就是me/left/right这三者，所以根据访问它们的顺序，划分出了三种顺序，首先是先左后右，其次是me放在哪个位置，根据me的位置对遍历顺序进行命名，me在前即前序，在中即中序，在后即后序。

二、递归遍历的实现

　　递归是符合我们的思维习惯的，一个复杂的问题总是可以分解为若干简单的问题。无论一棵树多么庞大，我从它的根节点出发，看到的是最多３个节点：我自己，我的左孩子，我的右孩子。我自己可以直接访问，然后是访问左孩子和右孩子。访问左孩子和右孩子的方法是一样的，访问它们自己节点，以及它们的左右孩子。这就是递归，这就是分治，把一个问题分解为几个子问题，分别考虑每个子问题，如果子问题跟我的处理逻辑一样，那么就成了递归。

// 这里以前序遍历为例，中序/后序只需要调整visit(node)所在位置即可
void traverse(node_t *node) {visit(node);traverse(node->left);traverse(node->right);
}

　　但是递归存在一个问题：如果树很深，那么函数的栈可能溢出。通常情况下栈的大小是固定的，不会动态扩展（go语言除外，它的栈可以伸缩，所以用go写递归，不用考虑栈溢出的问题）。每调用一个函数，就消耗一定的函数栈空间，如果这个函数没有结束，那么它会一直占用栈空间；在这个函数内部调用一个函数，又开辟了新的栈空间，如果树太深，那么栈就可能耗尽，然后访问越界，发生踩内存，coredump等未知问题。

　　所以，我们需要非递归，至少我们可以仿照函数栈的方式，自己实现栈，组织树的节点，完成遍历。当树太深的时候，我们可以动态扩展栈的空间，最终完成树的遍历。怎么实现栈的动态扩展，网上可以找到很多相关介绍。我的另外一篇博客实现了一种栈扩展的方法。在这里，只需要知道栈怎么用的：push/pop，后进先出，不考虑栈空间的扩展问题（假设它已经可以自动扩展了）。

三、怎么设计出非递归遍历算法

　　函数栈实现了递归，我们需要用自己的栈替换掉函数的栈，组织树的节点。一开始，我尝试分析函数栈的过程，发现太复杂了。函数栈很通用，一个节点会反复的入栈出栈，栈中的元素带了状态信息，这些状态信息就是我们的栈变量，所以每次处理当前栈顶元素的时候，总是可以知道应该做什么。以上面的前序递归函数为例，执行函数traverse(node)，首先需要访问node这个节点，于是开辟新的函数栈调用函数visit(node)，当visit结束后，重新回到traverse(node)，这时候pc指针已经指向了visit之后的代码，会调用traverse(node->left)。如果我们要用这种方式，那么需要压栈的时候，不仅把node入栈，还需要把node已经完成了多少工作也压栈，即

typedef enum {STATE_INIT,           // 刚刚开始STATE_VISITED_MYSELF, // 已经访问了自己STATE_LEFT_HANDLED,   // 已经处理了左孩子STATE_RIGHT_HANDLED,  // 已经处理了右孩子
} node_state_t;typedef struct {node_t *node;node_state_t state;
} node_info_t;

也就是说，每次入栈的元素是node_info_t，每次处理之后修改state信息，直到node_info_t处理完之后从栈里面弹出销毁。我没有继续走下去，我认为这么做是可以行得通的，但是比较复杂，显然我们知道的非递归遍历算法，只是把node压栈了，没有这么多信息入栈，所以需要寻找更简单的方法。我放弃了分析函数栈推导非递归算法这条路。

　　梳理一下思路：实现非递归遍历算法，需要用到栈，人工遍历是可以知道结果的。所以，我需要一张纸，一支笔，人工遍历，如果走到某一步发现走不下去了，看看可以怎么利用栈来帮我记录信息，然后重新开始，最终，应该可以找到一种方法，利用栈，实现非递归遍历。

　　设计遍历算法的步骤是：

　　　　1、明确遍历的顺序：前序、中序、还是后序；

　　　　2、人工遍历；

　　　　3、发现人工遍历进行不下去的时候，回头看看，怎么利用栈保存需要的信息；这一步可以总结出一些规则；

　　　　4、根据步骤3总结的规则，从步骤2重新开始，如此反复几次，应该就可以归纳出遍历的方法，最终完成遍历，并设计出一种算法。

四、推导非递归算法——前序遍历

（没有画图，感兴趣的朋友，可以自己找一张纸，一支笔，在纸上画画。下面的树只是用文字简单描述一下形状。）

                     <00>/\<01>                    <02>/\                      /\<03>        <04>        <05>        <06>/\          /\          /\          /\ 
<07>  <08>  <09>  <10>  <11>  <12>  <13>  <14>

　　明确遍历顺序：我->左->右。

　　开始遍历：00->01->03->07->?，当遍历到07的时候，已经没有左子树了，遍历不下去了。我们知道下一个应该遍历08，我们用栈可以用。08是03的右孩子，所以遍历03的时候应该把08压入栈。制订规则1：当遍历访问某个节点的时候，把它的右孩子入栈。这条规则是否有什么问题，暂且不管，如果最终发现遍历结果有问题，我们再回头来调整已经制订的规则，暂且用它。

　　已经有一条规则，现在重新遍历，同时准备一个栈，每次遍历到一个节点，都把它的右孩子入栈（如果它有右孩子）：

　　开始遍历：00->01->03->07（07没有有孩子，不压栈）->?现在可以出栈了，正好是08出栈，符合预期……

　　栈空间：|->02->04->08

　　刚才的问题已经解决，重新整理一下草稿纸，继续：

　　开始遍历：00->01->03->07->08(出栈)->04(出栈,压10)->09->10(出栈)->02(出栈,压06)->05->11->12->06(出栈,压14)->13->14

　　栈空间：|->(出02)->(出04)->(出08)->(出10)->(出06)->(出12)->(出14)。

说明：不方便展示入栈/出栈的全过程，需要自己手画。(出x)表示x曾经入栈，现已出栈。

至此，制订了一条规则，遍历可以完成。实际上，还有一条默认规则，手动遍历的时候，总是从一个节点（根节点）出发，打印自己，然后一路向左下方，直到没有左孩子为止，然后弹栈。这个过程中，每遍历到一个节点，把它的右孩子压栈（如果有右孩子）。

也就是说，根据上面提供的设计步骤，我们推导出前序遍历的非递归算法：

void
preorder(node_t *node)
{if (!node)return;stack_t *stk = NULL;// 当node为空的时候弹栈while (node || (node = stack_pop(&stk))) {visit(node);// 有右孩子就入栈if (node->right)stack_push(&stk, node->right);// 一路下去遍历左孩子node = node->left;}
}

备注：代码中用到的栈，请参考另外一篇博客。

五、推导非递归算法——中序遍历

　　明确遍历顺序：左->我->右。

开始遍历：00->...

一开始遍历，发现这里不对头，上面遍历到一个节点，可以立即访问遍历到的节点，那是前序遍历。中序遍历不能立即访问00，必须先访问它的左孩子，但是遍历需要从它经过。所以准备两条线索，一条线索描述走过的路径——遍历线，一条线索描述真正访问节点的顺序——访问线，访问线才是我们真正想要的结果。重新开始如下：

遍历线：00->01->03->07(07没有左孩子，可以访问它）。07之后，应该访问03，开始思考制订规则……

访问线：------------------07------

07之后应该访问03，所以遍历到03的时候应该把03压栈。另外遍历到07的时候，并没有把07压栈，因为07已经是叶子节点（没有左孩子了，它可以直接被访问了）。所以，制订规则如下：

1、一路往左往下走，走过的每个节点，如果还有左孩子，就把它压栈；如果没有左孩子，那么访问它，然后弹栈；

2、弹栈的节点不能继续往左遍历了，否则就重复了；（因为是往左往下走的过程压栈的节点，说明入栈的节点已经处理过左孩子了。）

3、弹栈的节点，直接访问它。（上述过程，把03压栈，07访问之后，03就应该出栈，出栈03立即访问它。这条规则是否正确，暂且不论，至少03这个点是正确的，之后如果发现这条规则有错，再重新考虑。所以我们的设计过程，就是基于遇到的情况尝试写出一条规则，然后基于规则从头开始，遇到问题时，修改我们的规则，这样周而复始不断尝试。）

基于已经制订的3条规则，重新开始如下（遍历过程请按照上述3条规则做）：

遍历线：00->01->03->07(不压)->03(出)。接下来怎么做？我们的规则，只说了弹出的节点，不用遍历它的左孩子，同时直接访问它，然后？

访问线：------------------07-----------03--------

栈空间：|->00->01->(出03)------

03出栈之后，访问03，然后应该访问03的右子树，03的右子树是08，08是叶子节点，可以直接访问。那么，如果出栈的是01呢，01的右孩子是04，04有左孩子，而且没有处理。所以这是更通常的一种情况，考虑这种情况应该怎么处理？根据上述规则，01出栈之后，不要遍历左孩子，直接访问01。之后呢？我们应该处理01的右子树04，但是从遍历04开始，继续一路向左向下，沿用之前的规则，遇到节点，压右孩子，遍历左孩子，直到遍历到左子树的叶子。所以，制订规则4（或者完善规则3）：弹栈的节点，先直接访问它，然后处理它的右孩子，处理方式参考已经制订的其他规则。（遍历它的左孩子，一路遍历和压栈……）

基于已经制订的规则，重新开始（03出栈后，先访问它，然后处理它的右孩子08，已经到了叶子，访问后再次弹栈……）：……重新梳理3条线的时候，发现自己凌乱了，画遍历线的时候，发现有些节点是从栈里面出来的，但是没有标注（出）这个字样，因为忘了。我想，可以甩锅给规则，规则不清晰，所以容易出错。因此，再次梳理上述的几条规则，让规则更加清晰一些。

重新梳理规则如下：

1、处理一个节点，如果它有左孩子：把该节点压栈，处理它的左孩子；

2、处理一个节点，如果它没有左孩子，但是有右孩子：访问该节点（例如打印它），处理它的右孩子；

3、处理一个节点，如果它没有左孩子，也没有右孩子：访问该节点，然后弹栈处理新的节点（来自于栈顶），处理方式参考这3条规则。

说明一下：重新梳理后的规则，首先是基于已有规则来梳理的，新规则的第2条是在梳理过程中变得明确的。上述三条规则相对于之前的规则，更加清晰，首先主题明确，怎么处理一个节点；其次，处理方式分了多种情况，分类是完备的，即3种情况涵盖了所有可能，任何一种可能都可以按照顺序归为情况1、或情况2、或情况3。

基于新的规则，重新开始人工遍历：

遍历线：00->01->03->07(规则3)->？发现出栈的节点，规则没有明确该怎么做，或者说规则出错了，因为按照规则1应该遍历它的左孩子

访问线：------------------07---

栈空间：|->00->01->(出03)->

（很抱歉，这是一篇很啰嗦的文章，如果我直接修改上面的规则，可能就看不到这个算法的设计推导过程了，一波三折的过程。）可以看到，梳理上述三条规则的时候，遗漏了之前的规则，弹栈的节点不能遍历左孩子，否则就重复了。

又一次修订规则：

1、处理一个非出栈的节点：

1.1、如果它有左孩子：把该节点压栈，处理它的左孩子；

1.2、如果它没有左孩子、有右孩子：访问该节点（例如打印它），处理它的右孩子；

1.3、如果它没有左孩子、没有右孩子：访问该节点，然后弹栈处理新的节点（来自于栈顶），处理方式参考第2条大规则。

2、处理一个出栈的节点：

2.1、（这不是一条规则，而是一条说明）它一定有左孩子：因为有左孩子的节点才会被压栈；

2.2、如果它有右孩子：访问该节点，处理它的右孩子；（处理方式跟规则1.2相同。）

2.3、如果它没有右孩子：访问该节点，然后弹栈处理新的节点。（处理方式跟规则1.3相同。）

不敢保证上述规则一定正确，但是可以重新开始了（严格按照规则去做，执行规格，我不如计算机，容易出错）：

遍历线：00->01->03->07->03->08->01->04->09->04->10->00->02->05->11->05->12->02->06->13->06->14

访问线：------------------07---03---08---01--------09---04---10---00---------------11---05--12---02---------13---06--14

栈空间：|->(出00)->(出01)->(出03)->(出04)->(出02)->(出05)->(出06)

按照规则遍历完所有树的节点，栈已经空了，再检查了一遍，发现没有问题。另外，遍历线没有标注（出），因为老是忘记，但这不影响结果的正确性，所以干脆不标注。

基于上述规则实现代码：

void
inorder(node_t *node)
{if (!node)return;stack_t *stk = NULL;int come_from_stack = 0;while (node) {// 非出栈节点的处理if (!come_from_stack) {// 有左孩子if (node->left) {stack_push(&stk, node);node = node->left;continue;}// 没有左孩子, 有右孩子if (node->right) { visit(node);node = node->right;continue;}// 没有左孩子和右孩子visit(node);node = stack_pop(&stk);come_from_stack = 1;continue;}// 出栈节点的处理come_from_stack = 0; // 每次清理标记, 弹栈的时候重新设置标记assert(node->left); // 一定有左孩子// 有右孩子if (node->right) {visit(node);node = node->right;continue;}// 没有右孩子visit(node);node = stack_pop(&stk);come_from_stack = 1;}
}

忠实于规则的代码实现了，但是看着不是那么满意。代码有点长，增加了一个标记come_from_stack，还有很多if-else，能否整理一下，让代码看起来更加简洁漂亮呢？首先还是应该从规则入手，上述规则能否简化？

回顾一下基于规则的人工遍历流程：

1、遍历左孩子压栈（这个过程不会处理节点），直到没有左孩子为止；

2、访问这个节点（它没有左孩子），然后访问它的右孩子（如果有），否则弹栈；

3、弹栈节点，一定有左孩子，但是已经遍历过了，不要处理它的左孩子，直接访问它，然后处理它的右孩子（处理方式回到步骤1）；如果没有右孩子，再次弹栈。

从一个节点的处理流程来说，是这样的：

1、是否要遍历它的左孩子：

1.1、要遍历的情况：它有左孩子，而且没有遍历过它的左孩子（即这个节点不是从栈里面来的），注意遍历左孩子前把它压栈；

1.2、不遍历的情况：它没有左孩子，或者它是来自于栈，已经遍历过它的左孩子了；

2、如果不遍历它的左孩子：直接访问它；

3、访问了这个节点之后，下一步怎么做？

3.1、如果它有右孩子，回到步骤1，处理它的右孩子，记住，这个新的节点不是弹栈的节点；

3.2、如果没有右孩子，弹栈，回到步骤1，记住，这个新节点是弹栈的节点。

关于下一个节点来源问题：可以封装一个函数，专门获取下一个节点，逻辑很简单——如果node非空，什么都不做；如果node为空，从栈中弹出一个节点，同时设置标记，表示节点来自于栈。经过流程梳理之后，可以按照下面的方式实现代码：

// 注意: stack可以动态扩展, 扩展的时候stack指针会变化, 所以需要传递二级指针
static inline node_t*
get_next_node(node_t *node, stack_t **pstk, int *come_from_stack)
{// 如果node为空, 从栈中弹出nodeif ((*come_from_stack = !node))node = stack_pop(pstk);return (node);
}void
inorder(node_t *node)
{if (!node)return;stack_t *stk = NULL;int come_from_stack;while (get_next_node(node, &stk, &come_from_stack)) {// 如果有左孩子, 而且该节点不是来自于栈, 则遍历左孩子if (node->left && !come_from_stack) {stack_push(&stk, node);node = node->left;continue;}// 不需要处理左孩子, 直接访问这个节点visit(node);/* 如果有右孩子, 下一次处理右孩子;* 如果没有右孩子(node->right为NULL), 下次从栈弹出 */node = node->right;}
}

重新梳理流程之后，代码看起来要好多了。

六、推导非递归算法——后序遍历

后序遍历简单说明下推导过程中遇到的一些问题，不再详细推导。上面二叉树的图离得太远了，所以先自行在纸上画出二叉树的图。

首先明确顺序：左->右->我。然后沿左子树一路遍历到底，因为底部的节点7没有右孩子，所以可以访问7；然后应该访问8，所以想到应该提前把8压栈，8是3的右孩子，所以沿左子树遍历过程中把节点的右孩子压栈，重新来过。会发现，只压右孩子是不行的，因为右孩子完了之后，需要它的父节点，所以干脆直接把遍历到的节点压栈，自然可以找到它的右孩子。所以，规则1是延左子树遍历过程中把途经节点压栈，直到到达叶子节点，访问叶子节点。

访问叶子节点之后，需要弹栈。弹出的节点，显然不能遍历左孩子了。应该先处理右孩子，假设右孩子是一颗树，那么按照规则1处理即可。然而问题来了，出栈的那个节点丢失了，处理完右子树之后，应该处理之前出栈的节点，即右子树的父节点。但是找不到它了。所以，出栈的节点如果有右子树，先把自己重新压栈，再处理右子树（因为顺序是左->右->我），当右子树处理完了之后，出栈处理自己。

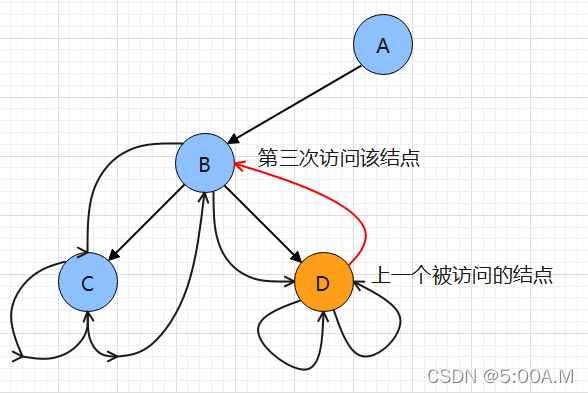
那么，出栈的节点究竟应该怎么处理？因为，出栈的节点，可能刚刚遍历了它的左子树，那么它出栈了，应该处理它的右孩子；也有可能，出栈的节点进入栈2次，已经处理过右孩子，那么应该直接访问它。

所以，我们需要知道出栈的节点，究竟处理了有没有处理过右孩子。最直接的想法是，增加一个状态信息，记录入栈节点的状态。但是，这需要新增一个数据结构来记录，这就涉及到为数据结构分配内存，以及释放内存等相关处理，会增加一定的代码量，这些代码只是针对这个问题而编写，几乎不会被其他地方复用，没有太大价值。可以有另外一种方式，设原来的栈为栈A，再新增一个栈B，如果一个节点从栈A出来之后，发现它需要重新入栈（因为它有右孩子，需要先处理右孩子，然后再处理它自己），那么把节点同时入栈A和栈B，所以出栈的时候，先从栈A出，然后拿出栈的节点跟栈B的顶部节点比较，如果相同，那么说明该节点入栈两次，即说明它的右子树已经被处理。这时候把栈B的节点也出栈，即一个节点从两个栈出，则说明它的左右子树都被处理了；如果只从一个栈出，说明只有左孩子被处理，右孩子没有被处理。另外，可以从入栈的时候来看这条规则，入栈的时候，如果在处理左子树的时候入栈，则入栈A（从栈A出表示左子树已经被处理过了）；如果遍历到底部，这个节点没有左子树，但是有右子树，那么节点同时入栈A和栈B（入栈A表示左子树被处理过，因为它没有左子树，所以也可以等价认为已经被处理过）。

整理下栈A和栈B入栈规则：

1、一个节点如果没有左右孩子（叶子节点），那么可以直接访问它；

2、如果有左孩子，且左孩子没有被遍历，那么把它放入栈A；

3、如果从栈A出来（或者没有左孩子，视为左孩子被遍历过了）之后，发现它有右孩子，那么这个节点同时入栈A和B，然后处理它的右孩子；

4、如果从栈A出来（或无左孩子），但是没有右孩子，那么直接处理这个节点。

5、如果同时从栈A和B出来，说明左右孩子都被处理过了，那么直接处理这个节点。

说明一下：

1、新增一个栈B，相当于给节点新增一个状态信息，但是不需要新增结构，复用原来的栈就ok了。

2、一个节点同时入栈A和B，当从栈A出来的时候，一定可以从栈B出来。因为这个节点同时进入栈A和B，此时它们位于两个栈的底部，然后处理它的右子树，它的右子树处理过程中可能入栈一些节点，但是当右子树处理结束的时候，所有入栈的节点应该都已经处理完了。如若不然，右子树就还没有处理完。

没有进一步整理规则，附上代码：

static inline node_t*
get_next_node(node_t *node, stack_t *stk_arr[2], int *from_stk_times)
{*from_stk_times = 0;if (!node) {node = stack_pop(&stk_arr[0]);if (node) {*from_stk_times += 1;if (node == stack_top(&stk_arr[1])) {*from_stk_times += 1;stack_pop(&stk_arr[1]);}}}return (node);
}void
postorder(node_t *node)
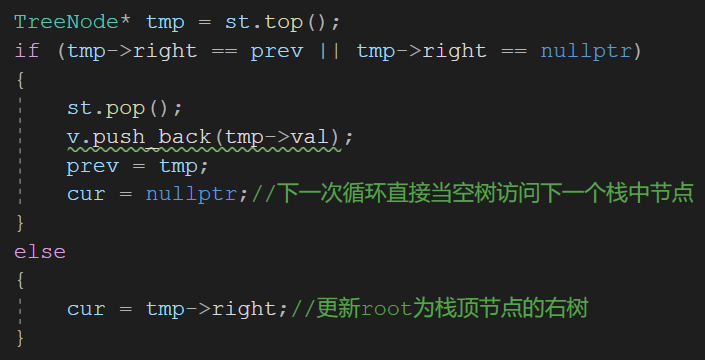
{if (!node)return;stack_t *stk_arr[2] = { NULL };int from_stk_times;while ((node = get_next_node(node, stk_arr, &from_stk_times))) {// 遍历左子树if (node->left && from_stk_times == 0) {stack_push(&stk_arr[0], node);node = node->left;continue;}// 处理右子树if (node->right && (!node->left || from_stk_times == 1)) {stack_push(&stk_arr[0], node);stack_push(&stk_arr[1], node);node = node->right;continue;}// 访问当前节点visit(node);node = NULL;}
}

一支笔，一张纸，所以附一张图：要理解这个过程，动手画一画挺重要，可以加深理解。