一.前序遍历（根左右）

1.思路图解

循环处理条件为栈是否为空或当前结点是否为空

第一次遍历根结点1且根结点入栈，然后循环处理当前根结点的左子树，当根结点及根的左子树处理完后，开始处理以栈中结点的右子树为根结点重复上述步骤，最终处理完成后后，list中的元素结果就是前序遍历的结果

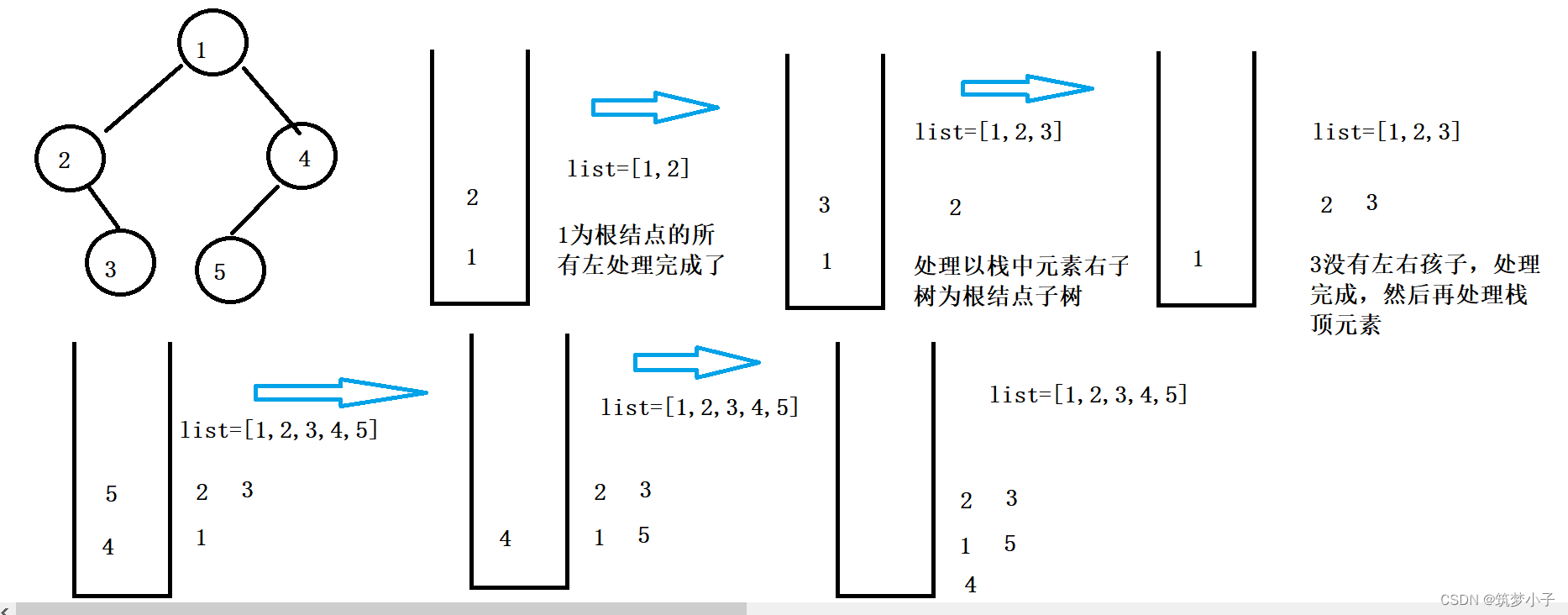
2.代码

 public List<Integer> preorderTraversal(TreeNode root) {Stack<TreeNode> stack = new Stack<>();List<Integer> list = new ArrayList<>();TreeNode node = root;while(!stack.empty() || node!=null) {//一直处理当前结点的左子树，左孩子处理完后入栈while(node!=null) {list.add(node.val);stack.push(node);node = node.left;}//左子树处理完，处理栈顶元素的右子树（根节点和左子树已经处理完）node = stack.pop().right;}return list;}

二.中序遍历（左根右）

1.思路图解

先处理以当前结点为根的所有左孩子（入栈），当所有的左孩子处理完成后，这时候栈顶元素就是最左边的孩子，然后处理该元素（放到集合中），接着以该元素为根节点再重复上面的步骤，最终集合结果就是中序遍历.

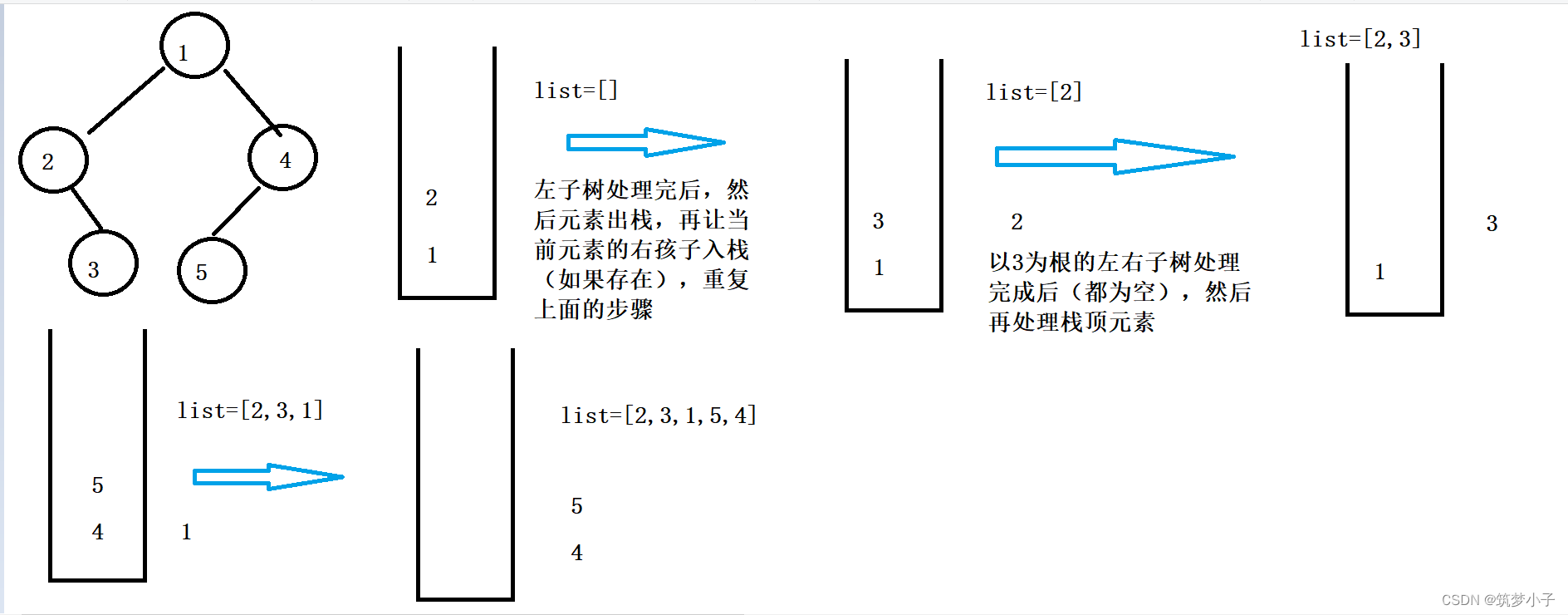
2.代码

public int[] inorderTraversal (TreeNode root) {// write code hereList<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while(!stack.isEmpty() || cur!=null) {//先处理所有的左子树中的节点while(cur!=null) {stack.push(cur);cur = cur.left;}//处理栈中的根结点，然后再重复上面步骤处理以当前结点为根节点的子树TreeNode tmp = stack.pop();list.add(tmp.val);cur = tmp.right;}int[] res = new int[list.size()];for(int i=0; i<list.size(); i++) {res[i] = list.get(i);}return res;}

三.后序遍历（左右根）

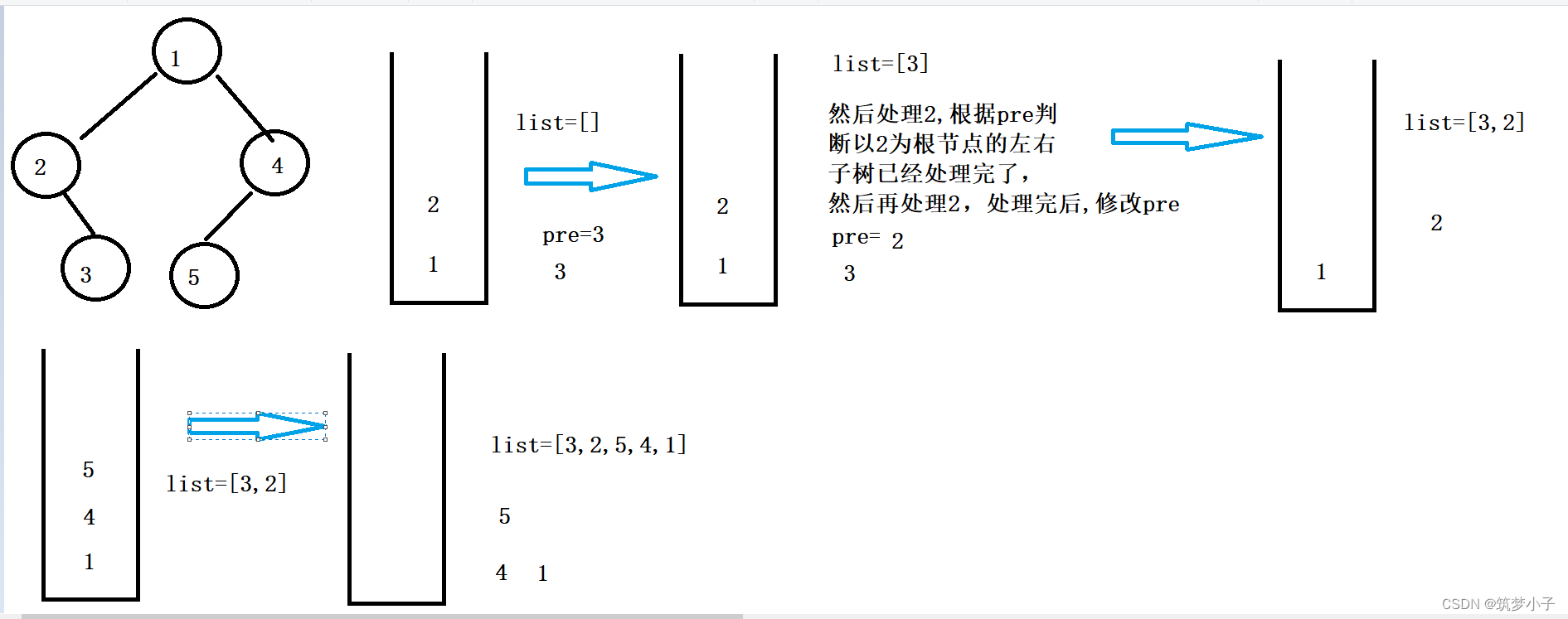
1.思路图解

先处理根的左右子树，由于在处理到右子树的时候，会回溯到父节点，所以需要借助一个前驱结点来记录当前结点的右子树是否已经遍历过了，如果当前结点的右子树已经遍历过，或者当前结点的右子树为空（这两种结果都说明以当前结点为根节点的左右子树都已经处理完了），这时候就需要处理当前结点，处理完当前结点后，记录前驱结点为当前结点，然后将当前结点置为空（置空说明当前结点的左右子树都已经处理完成了）

2.代码

    public int[] postorderTraversal (TreeNode root) {// write code hereTreeNode pre = null;//标记右子树是否访问过TreeNode cur = root;Stack<TreeNode> stack = new Stack<>();ArrayList<Integer> list = new ArrayList<>();while(cur!=null || !stack.empty()) {//将左子树的所有节点放到栈中while(cur != null) {stack.push(cur);cur = cur.left;}//查看栈顶元素的是否存在右子树，如果存在，是否已经访问过cur = stack.peek();if(cur.right == null || pre==cur.right) {//说明当前结点没有右子树或者右子树已经处理了//这时候就可以处理当前根结点了stack.pop();list.add(cur.val);pre = cur;cur = null;}else {//说明当前节点的右子树没有处理，继续处理cur = cur.right;}}int[] res = new int[list.size()];for(int i=0; i<list.size(); i++) {res[i] = list.get(i);}return res;}

四.层序遍历

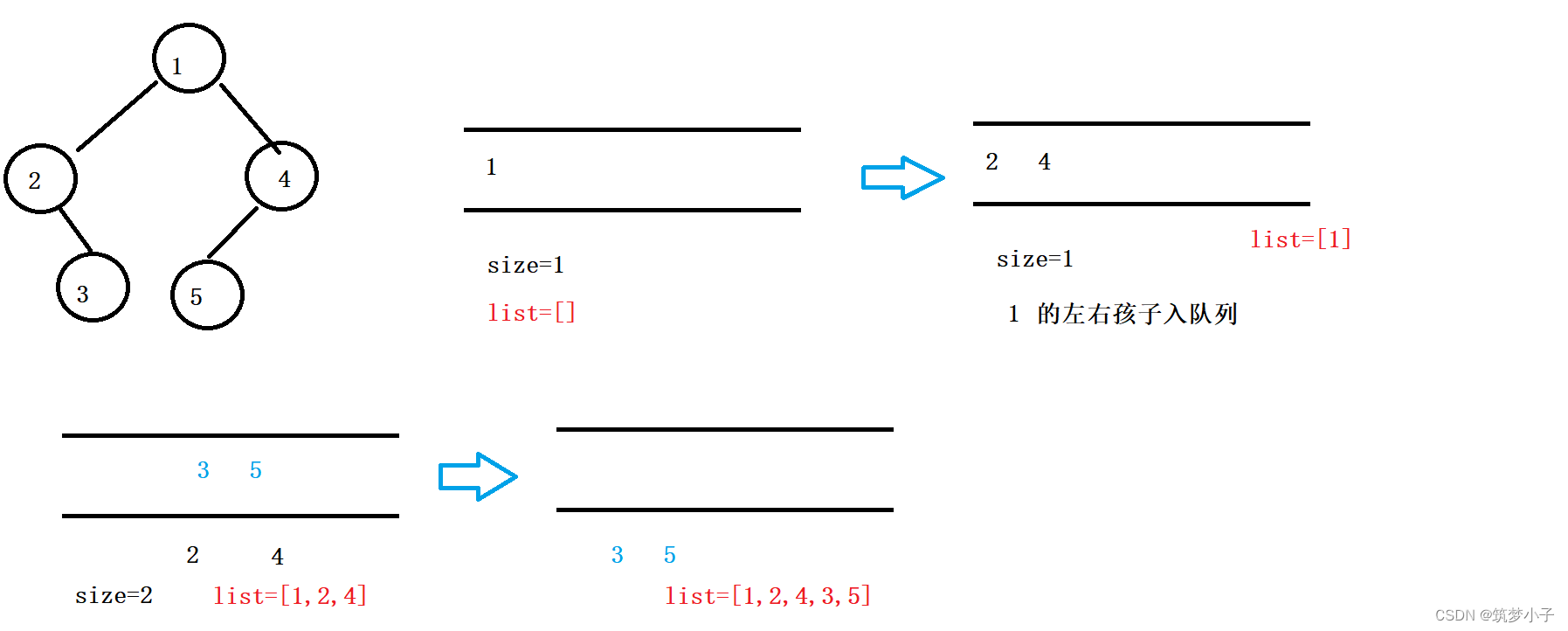
1.思路图解

借助队列先进先出的原理，实现每一层元素的遍历，在遍历当前层元素的时候，首先需要获取队列当前的大小，因为初始时队列中元素是只有一层元素，在出队列的时候之后可能会有元素入队列，在处理当前层元素的时候，需要判断当前元素的左右孩子是否存在，如果存在，就入队列，因为队列需要保存下一层元素；之后集合中的结果就为层序遍历的结果。

2.代码

 public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {ArrayList<ArrayList<Integer>> res = new ArrayList<>();//空树，直接返回if(root == null) {return res;}//借助队列实现层序遍历Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while(!queue.isEmpty()) {//计算当前一层元素的个数，之后根据该大小出队列int size = queue.size();//使用list保存当前层的元素个数ArrayList<Integer> list = new ArrayList<>();for(int i=0; i<size; i++) {TreeNode tmp = queue.poll();list.add(tmp.val);//处理当前结点的左右子树if(tmp.left != null) {queue.offer(tmp.left);}if(tmp.right != null) {queue.offer(tmp.right);}}//将当前层元素添加到结果集中res.add(list);}return res;}