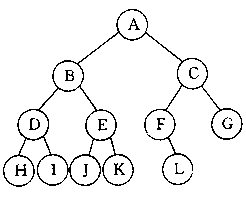
默认给一棵树前序遍历的结果，按要求创建这棵树（#表示空），并用非递归的方法对它进行遍历。

解题思路

1.递归遍历： 则将二叉树的遍历看作是分治问题，将每一棵树都分为根-左子树-右子树三部分，每部分按同样的方法递归遍历即可。具体实现见下篇博客 二叉树的实现&递归遍历
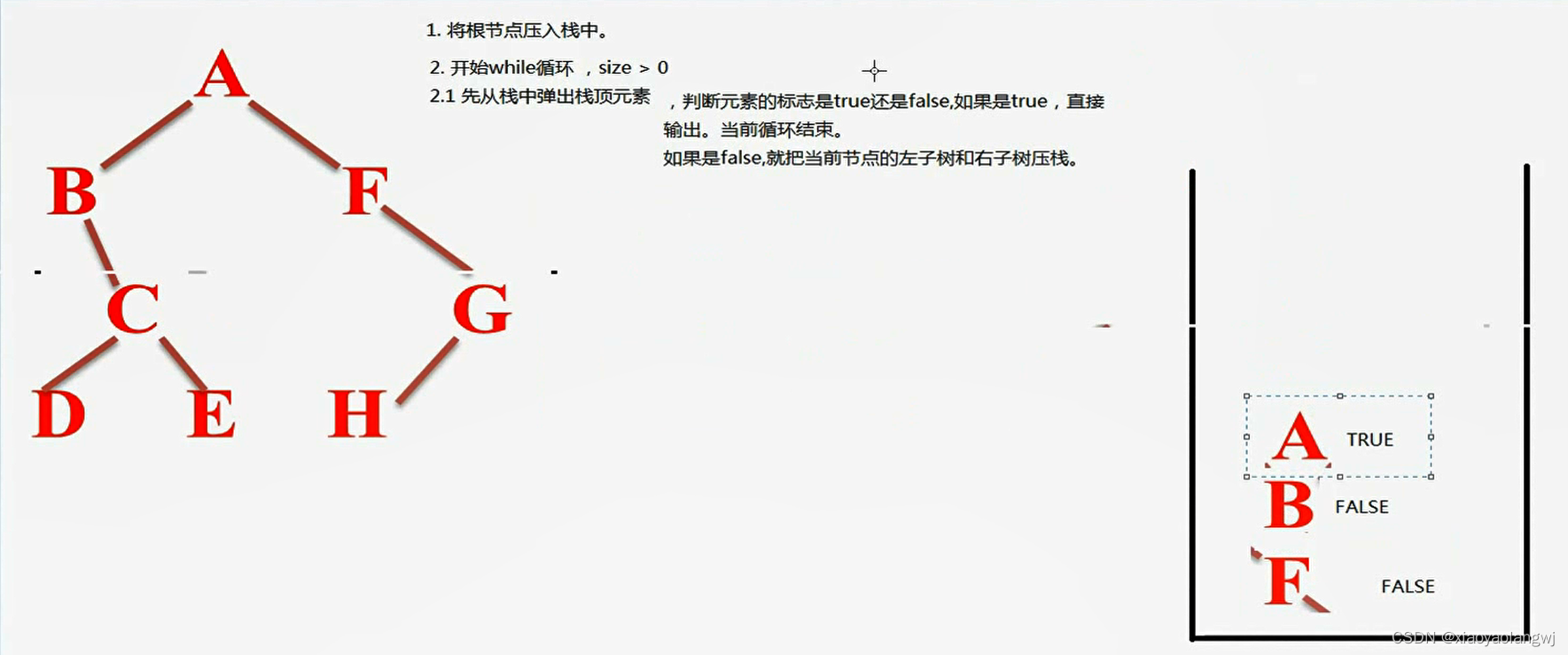
2.非递归遍历：我们可以借用栈的知识完成树的遍历。使用栈完成的过程以下面的前序遍历为例

前序： 根–> 左–> 右
主要思路：若根节点有效则输出并入栈；访问其左子树遇到根节点输出并入栈直到根节点下再无左子树，将栈顶元素出栈，并继续访问它的右子树；直至栈内无元素且当前元素无效，遍历结束。
具体过程如下：

1.根节点A有效则输出并入栈，访问A左树（输出条件：当前根节点有效；也是入栈条件）
2.B有效则输出并入栈，访问B左树
3.D有效则输出并入栈，访问D左树
4.D左树为空，当前栈顶D出栈，访问D右树（出栈条件：左树/右树 为空，栈顶元素出栈）
5.D右树为空，当前栈顶B出栈，访问B右树
6.E有效则输出并入栈，访问E左树
7.E左树为空，当前栈顶E出栈，访问E右树
8.F有效则输出并入栈，访问F左树
9.F左树为空，当前栈顶F出栈，访问F右树
10.F右树为空，当前栈顶A出栈，访问A右树
11.C有效则输出并入栈，访问C左树
12.C左树为空，当前栈顶C出栈，访问C右树
13.C右树为空，栈内无元素 （结束条件：栈内无元素，或者当前元素为空）
遍历结束！！

实现前序的代码如下所示：

//前序：A  B  D  E  F  C
while (StackEmpty(&st) != 0 || cur != NULL)  //循环条件：与（栈内无元素，或者当前元素为空）相反
{while (cur != NULL)  //输出/入栈条件：当前节点不为空{printf("%c ", cur->_data);  //输出StackPush(&st, cur);  //入栈cur = cur->_left;  //访问节点左子树}BTNode* top = StackTop(&st);  //找到栈顶元素StackPop(&st);   /出栈条件：左树/右树 为空，栈顶元素出栈cur = top->_right;  //访问右子树
}

中序： 左 --> 根 --> 右

//中序：D  B  E  F  A  C
while (StackEmpty(&st) != 0 || cur != NULL) //当栈不为空或当前节点有效，循环继续{while (cur != NULL)  //当前节点不为空{StackPush(&st, cur); //节点入栈cur = cur->_left;  //访问左子树}BTNode* top = StackTop(&st);  //找到栈顶元素printf("%c ", top->_data);  //输出栈顶元素StackPop(&st);  //栈顶元素出栈cur = top->_right;  //访问右子树}

后序： 左 --> 右 --> 根
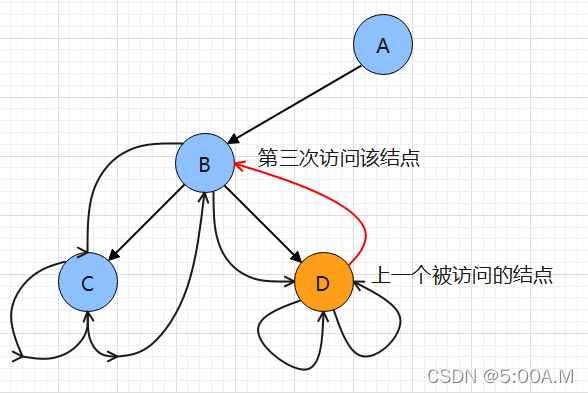
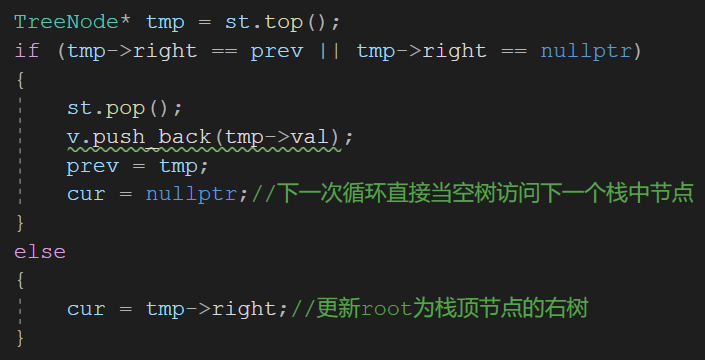
注意：要判断此时访问的结点之前是否访问过！！

//后序：D  F  E  B  C  A
BTNode* prev = NULL;
while (cur || StackEmpty(&st) != 0){while (cur != NULL){StackPush(&st, cur);  //入栈cur = cur->_left;  //访问左子树}BTNode* top = StackTop(&st);if (top->_right == NULL || top->_right == prev) //右子树为空，或者已经访问过{StackPop(&st);  //栈顶元素出栈printf("%c ", top->_data); //输出prev = top;}else cur = top->_right;}

完整代码

BT.h – 头文件

#define _CRT_SECURE_NO_WARNINGS 1
#ifndef __TREE_H__
#define __TREE_H__ #include <stdlib.h>
#include <stdio.h>
#include <assert.h>
#include <string.h>typedef char BTDataType;
typedef struct BinaryTreeNode   //树节点定义
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;//创建树
BTNode *BinaryTreeCreate(BTDataType*a, int*pi);
//销毁树
void BinaryTreeDestory(BTNode* root);
//非递归遍历
void BinaryPrevOrder(BTNode* root);  //前序
void BinaryInOrder(BTNode* root);   //中序
void BinaryPostOrder(BTNode* root);   //后序
//测试类
void Test();typedef BTNode* STDataType;
typedef struct Stack   //栈定义
{STDataType* _a;int _top;int _capacity;
}Stack;//栈的操作
void StackInit(Stack* ps);  //初始化
void StackDestory(Stack* ps);  //销毁
void StackPush(Stack *ps, STDataType x);  //入栈
void StackPop(Stack* ps);  //出栈
STDataType  StackTop(Stack* ps);  //取栈顶元素
int StackEmpty(Stack* ps); //判断栈空
int StackSize(Stack* ps);  //判断栈内元素
void StackPrint(Stack* ps);   //栈节点输出#endif//__TREE_H__

BT.c – 树的操作

#define _CRT_SECURE_NO_WARNINGS 1
#include "BT.h"BTNode *BinaryTreeCreate(BTDataType*a, int* pi)  //创建树
{if (a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->_left = root->_right = NULL;root->_data = a[*pi];(*pi)++;root->_left = BinaryTreeCreate(a, pi);root->_right = BinaryTreeCreate(a, pi);return root;
}void BinaryTreeDestory(BTNode* root)  //销毁树
{if (root){BinaryTreeDestory(root->_left);BinaryTreeDestory(root->_right);free(root);root = NULL;}
}void BinaryPrevOrder(BTNode* root)  //前序遍历
{Stack st;StackInit(&st);BTNode* cur = root;while (StackEmpty(&st) != 0 || cur != NULL){while (cur != NULL){printf("%c ", cur->_data);StackPush(&st, cur);cur = cur->_left;}BTNode* top = StackTop(&st);StackPop(&st);cur = top->_right;}
}void BinaryInOrder(BTNode* root)  //中序遍历
{Stack st;StackInit(&st);BTNode* cur = root;while (StackEmpty(&st) != 0 || cur != NULL){while (cur != NULL){StackPush(&st, cur);cur = cur->_left;}BTNode* top = StackTop(&st);printf("%c ", top->_data);StackPop(&st);cur = top->_right;}
}void BinaryPostOrder(BTNode* root)  //后序遍历
{BTNode* cur = root;BTNode* prev = NULL;Stack st;StackInit(&st);while (cur || StackEmpty(&st) != 0){while (cur != NULL){StackPush(&st, cur);cur = cur->_left;}BTNode* top = StackTop(&st);if (top->_right == NULL || top->_right == prev){StackPop(&st);printf("%c ", top->_data);prev = top;}else cur = top->_right;}
}void Test()  //测试
{char a[20] = "ABD##E#H##CF##G##";int pi = 0;int i = 0;BTNode* root = BinaryTreeCreate(a, &pi);printf("树创建成功！\n");printf("树前序遍历的结果是： ");BinaryPrevOrder(root);printf("\n");printf("树中序遍历的结果是： ");BinaryInOrder(root);printf("\n");printf("树后序遍历的结果是： ");BinaryPostOrder(root);printf("\n");BinaryTreeDestory(root);printf("销毁成功！\n");
}

ST.c – 栈的操作

#define _CRT_SECURE_NO_WARNINGS 1
#include "BT.h"void StackInit(Stack* ps)  //栈的初始化
{assert(ps);ps->_a = NULL;ps->_capacity = 0;ps->_top = 0;
}void StackDestory(Stack* ps)  //栈的销毁
{assert(ps);ps->_capacity = 0;ps->_top = 0;free(ps->_a);ps->_a = NULL;
}void StackPush(Stack *ps, STDataType x)  //入栈
{assert(ps);if (ps->_top == ps->_capacity){size_t newcapacity = (ps->_capacity == 0 ? 4 : ps->_capacity * 2);ps->_a = (STDataType*)realloc(ps->_a, sizeof(STDataType)*newcapacity);ps->_capacity = newcapacity;}ps->_a[ps->_top] = x;ps->_top++;
}void StackPop(Stack* ps)  //出栈
{assert(ps&&ps->_top>0);ps->_top--;
}STDataType  StackTop(Stack* ps)  //取栈顶元素
{assert(ps&&ps->_top>0);return ps->_a[ps->_top - 1];
}int StackEmpty(Stack* ps)  //判断栈是否为空
{assert(ps);if (ps->_top == 0)return 0;else return 1;
}int StackSize(Stack* ps)  //判断栈内元素
{assert(ps);STDataType size = ps->_top;return size;
}void StackPrint(Stack* ps)  //输出栈内元素
{assert(ps);while (StackEmpty(ps) != 0){printf("%d ", StackTop(ps));StackPop(ps);}printf("\n");
}

main.c – 主文件

#define _CRT_SECURE_NO_WARNINGS 1
#include "BT.h"int main()
{printf("      *******二叉树的实现******\n");Test();printf("\n");system("pause");return 0;
}