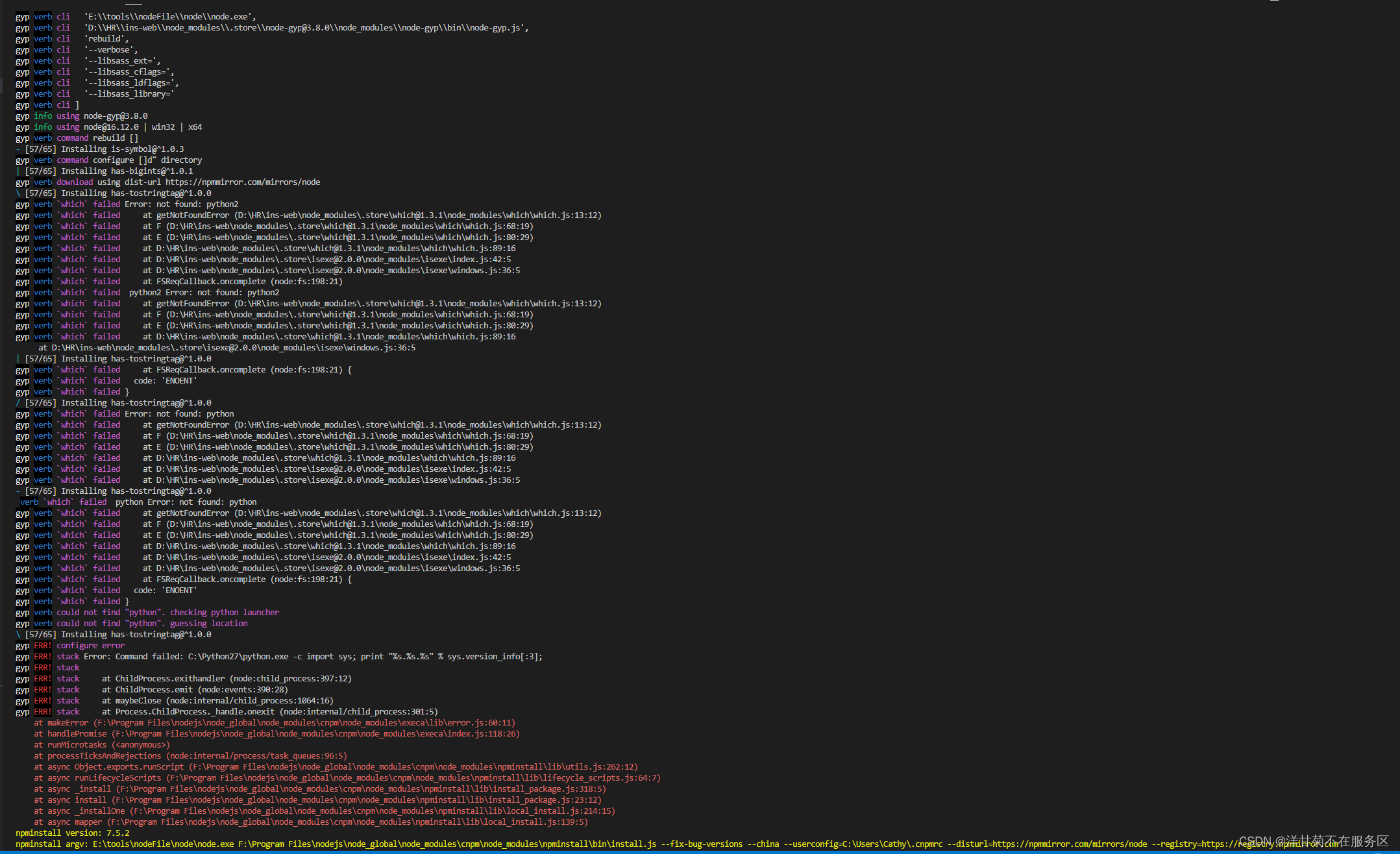
稀疏矩阵:
当一个矩阵中的很多元素都是零,而且非零元素的分布没有规律时,该矩阵称为稀疏矩阵。
稀疏矩阵的压缩存储方法:
从稀疏矩阵的概念,我们可以知道,稀疏矩阵的大多元素都是零。所以,我们只需要存储非零元素即可。这时,我们引入三元组表的概念:三元组表是一个线性表,线性表中的每一个结点对应稀疏矩阵的一个非零元素。结点包括三个域,分别为非零元素的行下标、列下标和值。并且,结点按矩阵的行优先顺序排列。
【例】存在矩阵A。那么矩阵A是怎么存储的呢?
A矩阵的三元组表:索引为0时,存储的是稀疏矩阵的行数、列数和非零元素的个数。
索引
i
j
v
0
5
6
6
1
1
1
3
2
1
6
7
3
2
3
6
4
3
1
2
5
3
2
3
6
5
5
2
表中结点类型定义如下:(JAVA)
package com.linearList.matrix; /* * 说明: 三元组的结点描述 * @author 秦霞爱朱剑锋 */ public class Node { int i; // 行下标 int j; // 列下标 int value; // 值 public Node() {} public Node(int i, int j, int vlaue) { this.i = i; this.j = j; this.value = vlaue; } }
矩阵类型定义如下:
package com.linearList.matrix; /** 说明:矩阵的压缩存储描述(行优先)*/ public class Matrix {final int MAX = 10; // 非零元素个数的最大值int rows, cols, vals; // 分别为行、列、非零元素个数Node data[] = new Node[MAX];public Matrix(int rows, int cols, int vals) {this.rows = rows;this.cols = cols;this.vals = vals;// 初始化data[0]:data[0]的i,j,v分别存储稀疏矩阵的行数、列数和非零元素的个数data[0] = new Node(rows, cols, vals);// 申请剩余空间if(vals <= MAX) {for (int i = 1; i <= vals; i++) {data[i] = new Node();}}} }
矩阵的转置运算:

A的三元组表
索引
i
j
v
0
5
6
6
1
1
1
3
2
1
6
7
3
2
3
6
4
3
1
2
5
3
2
3
6
5
5
2
B的三元组表
索引
i
j
v
0
5
6
6
1
1
1
3
2
1
6
7
3
2
3
6
4
3
1
2
5
3
2
3
6
5
5
2
也就是说,矩阵的转置实际上是三元组表的改变。
【算法一】
算法思路:
①将两个矩阵的行数和列数相互交换;
②将每个三元组中的i和j互相调换;
③重排三元组之间的次序。
代码实现:(JAVA)
// 稀疏矩阵的转置 public static Matrix transpose(Matrix a) { Matrix b = new Matrix(a.cols, a.rows, a.vals); // 转置后的矩阵b int bindex = 1; for(int col = 1; col <= a.cols; col++) { // 按a的列序转置 for(int aindex = 1; aindex <= a.vals; aindex++) { // 扫描整个三元组表 if(a.data[aindex].j == col) { b.data[bindex].i = a.data[aindex].j; b.data[bindex].j = a.data[aindex].i; b.data[bindex].value = a.data[aindex].value; bindex++; } } } return b; }
核心代码讲解:
①我们遍历矩阵a的列序,保证转置之后的矩阵行优先的原则。
②扫描整个三元组,找到当前列的结点。(此时,浪费了一定的时间。因为对于每一个col,我们都需要遍历整个三元组,直到与其对应的为止。)
算法评价:
上述算法是在二重循环内完成的,算法的时间复杂度为O(cols*vals)。当非零元素的个数值vals=cols*rows时,时间复杂度为O(
)。可见,该算法虽然节省了空间,但时间复杂度提高了。所以,上述算法只适用于当vals<<rows*cols(非零元素较少)的情况。
【算法二:快速转置算法】
原理:
我们已经知道,矩阵的转置实际上是改变其对应的三元组。那么,我们事先能不能知道改变之后的三元组是什么样子呢?答案是肯定的。进一步,既然我们已经知道了转置之后的三元组,那么对于索引为1的第一个非零元素,我们可不可以直接确定它转置之后再哪一个位置呢?同理,索引为2的第二个非零元素,我们能不能直接确定它转置之后的位置呢?以此类推,如果我们知道了这样一个映射关系,我们就可以做到直接定位,把结点插入到新的位置。
举个例子:
我们去图书馆找书的时候,我们不会从图书馆的第一个书架开始,一本一本的去找。我们是怎么做的呢?根据书的编号,参考图书馆存放书的信息,直接定位到相应的书架去找!那么,在这个例子中,图书馆为大家提供的馆藏信息表(记录不同的书的存放位置)就显的很重要了。这个表,实际上就是一个映射关系。
那么,如果我们也构建这样一个映射关系表,是不是也可以做到直接定位了呢?答案是肯定的。
如何构建这样一个映射关系?
第一列的元素转置之后在第一行。那么如果第一列的非零元素有两个,那么他们肯定占据的是索引1和2位置。同理,第二列的非零元素如果有两个,占据的应该是索引3和4位置。以此类推,我们便可以确定转置之后的位置了。因此,我们需要记录:每一列非零元素的个数num[col]以及该列第一个非零元素的起始索引位置cpot[col]。
这里,还是以矩阵A举例。
col
1
2
3
4
5
6
num[col]
2
1
1
0
1
1
cpot[col]
1
3
4
5
6
从表格我们可以发现:cpot[col]=cpot[col-1]+num[col]
算法思路:
①构建映射关系。即初始化num[col]和cpot[col]。
②将结点放到指定的位置。
代码实现:
// 稀疏矩阵的快速转置算法 public static Matrix fastTranspose(Matrix a) {Matrix b = new Matrix(a.cols, a.rows, a.vals);int num[] = new int[a.cols + 1];// 初始化 num[]for(int i = 1; i < a.vals; i++) {++num[a.data[i].j];}int cpot[] = new int[a.cols + 1];// 初始化 cpot[]cpot[1] = 1;for(int col = 2; col < num.length; col++) {cpot[col] = cpot[col-1] + num[col];}for(int index = 1; index <= a.vals; index++) {int col = a.data[index].j;int newIndex = cpot[col];b.data[newIndex].i = a.data[index].j;b.data[newIndex].j = a.data[index].i;b.data[newIndex].value = a.data[index].value;cpot[col]++;}return b; }代码讲解:
这里,初始化数组的时候,多开辟一个空间,是因为三元数组表的第一个元素)(索引为0的位置)存储的是矩阵的行数、列数以及非零元素的个数。
(欢迎评论指导!转载时,请注明出处,谢谢。)