一.矩阵快速幂

（1）矩阵定义

什么是矩阵运算呢？

在理解这个问题前，我们先要知道什么是矩阵

百度百科给的定义如下

矩阵是一个按照长方阵列排列的复数或实数集合

复数实数什么的我们先不管，总之，矩阵就是一堆数，按照矩形排列形成的集合
那么，我们所需要记录的也就是它的长、宽以及矩阵中存储的元素特殊的，长宽相等的矩阵我们定义它为方阵当两个矩阵的长宽相等时，我们认为这两个矩阵为同型矩形。

基本运算
矩阵的运算我们可以类比实数的运算来理解
在实数运算中，一般由进行运算的实数和运算符组成，运算符决定了运算类型
那么同样的，矩阵运算也是如此

（2）加法运算

首先，我们来看加法运算
两个矩阵进行一般的加法运算的前提是两个矩阵为同型矩阵
我们只需要将对应位置的元素相加即可，如下图
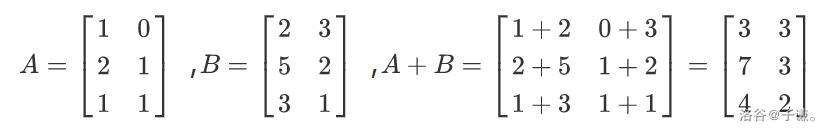
在这里插入图片描述

在矩阵的加法运算中，满足交换律和结合律，也就是
$A + B = B + A A + B = B + A$
$(A + B) + C = A + (B + C) (A + B) + C = A + (B + C)$
也许有人想问了，如果我想让两个非同型矩形进行相加可不可以实现呢？

答案是可以的，这种运算是被支持的，我们称这种运算为直和

但由于这种运算使用较少，且与本文关系不大，我们在此不多做解释，感兴趣的朋友可以阅览下面的链接，相信它会给你一个满意的答复

矩阵加法

（3）减法运算

在实数运算中，减法为加法的逆运算，同样的，在矩阵运算中也是如此，如下图

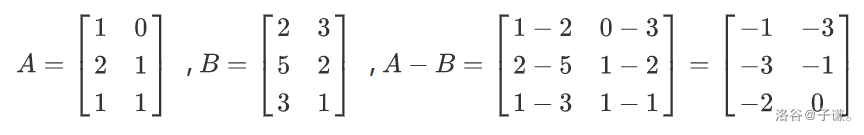
在这里插入图片描述

（4）数乘

在实数运算中我们并没有数乘这种运算（毕竟本身就是数，直接叫乘法了）

所以在数乘运算中，我们类比向量来进行理解

在数乘向量运算中，只需要将向量中的每个元素乘上那个数就可以了

数乘矩阵也是如此，如图

数乘矩阵运算中，满足如下运算律
$(\lambda\mu)A=\lambda(\mu A)(λμ)A=λ(μA)$
$(\lambda+\mu)A=\lambda A+\mu A(λ+μ)A=λA+μA$
$\lambda(A+B)=\lambda A+\lambda Bλ(A+B)=λA+λB$
矩阵乘法（矩阵乘矩阵）
在向量乘向量的运算中，是将每个元素与它对应的元素相乘，求所有乘积之和

那么矩阵乘矩阵是不是就是两个同型矩阵的对应元素相乘呢？

两个矩阵相乘的前提是前一个矩阵的列数等于后一个矩阵的行数

举个栗子， A为 nk矩阵， B 为 km 矩阵， C 为 m*n 矩阵，那么 A 可以与 BB 相乘， B 可以与 C 相乘， C 可以与 A 相乘，其他均不成立

我们知道了什么情况下两个矩阵可以相乘，那么他们怎么相乘呢？不讲每个对应位置相乘还能怎么乘呢？

设 A 为 n*k矩阵， B 为 k∗m 矩阵,那么它们的乘积 C 则为一个 n∗m 矩阵
$C_{i,j}=\sum_{r=1}^kA_{i,r}*B_{r,j}C _{i,j} $
是不是不太好理解，没关系看看图就知道了
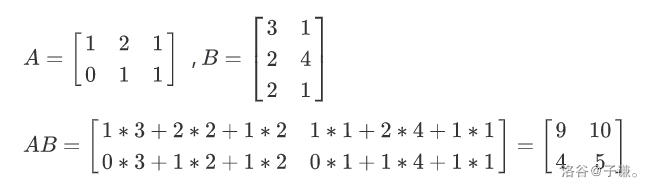
在这里插入图片描述

在矩阵乘法中满足以下运算律：
$(A B) C = a (B C) (A B) C = a (B C)$
$(A + B) C = A C + B C (A + B) C = A C + B C$
$C (A + B) = C A + C B C (A + B) = C A + C B$
在普通的乘法中，一个数乘1还是等于它本身，在矩阵乘法中也有这么一个“1”，它就是单位矩阵

不同于普通乘法中的单位1，对于不同矩阵他们的单位矩阵大小是不同的

对于 nm 的矩阵，它的单位矩阵大小为m∗m ，对于m∗n 的矩阵，它的单位矩阵大小为 nn

也就是说单位矩阵都是正方形的，这是因为只有正方形的矩阵能保证结果和前一个矩阵形状相同

单位矩阵的元素非0即1，从左上角到右下角的对角线上元素皆为1，其他皆为0

了解了这么多，我们开始看题

（5）P3390 【模板】矩阵快速幂

P3390 【模板】矩阵快速幂
题目背景
矩阵快速幂
题目描述
给定 n×n 的矩阵 A，求 A^k。
输入格式
第一行两个整数 n,k接下来 n 行，每行 n 个整数，第 i行的第 j的数表示A_i,j
输出格式
输出 A^k
共 n 行，每行 n 个数，第i行第 j 个数表示 (A^k)_i,j ，每个元素对 10⁹+7取模。
矩阵快速幂，由于矩阵乘法满足结合律，所以我们只需要把它按照一般的快速幂打，再重载一下运算符就可以了，好了我们直接放代码

#include<bits/stdc++.h>
using namespace std;
#define mod 1000000007
typedef long long ll;
const ll N=1e2+7;
ll n;
inline ll read()//快读
{ll a=0;ll f=0;char ch=getchar();while(!isdigit(ch)){f|ch=='-';ch=getchar();}while(isdigit(ch)){a=(a<<3)+(a<<1)+(ch^48);ch=getchar();}return f?-a:a;
}
struct node
{ll a[N][N];//下面的这个函数就是每次定义一个新的node类型的数的时候这个函数就会被调用node(){memset(a,0,sizeof a);}//每定义一个node类型的值的时候，就把a数组置零，不然之前的会将其覆盖inline void build(){for(int i=1;i<=n;i++)a[i][i]=1;//给a数组初始化（因为是矩阵乘法，要初始为1而不是0）}
}date;
node operator*(const node &x,const node &y)//重载乘法运算符
{node z;for(int k=1;k<=n;k++)//矩阵乘法是x的i,k乘以y的k,j;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)z.a[i][j]=(z.a[i][j]+x.a[i][k]*y.a[k][j]%mod)%mod;return z;
}
int main()
{ll k;n=read();k=read();for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)date.a[i][j]=read();node ans;ans.build();do{if(k&1)ans=ans*date;date=date*date;//重载的运算符*不能缩写为 * =k>>=1;}while(k);for(int i=1;i<=n;puts(""),i++)for(int j=1;j<=n;j++)cout<<ans.a[i][j]<<" ";return 0;
}

二.矩阵求斐波那契数列

P1962 斐波那契数列
题目背景
大家都知道，斐波那契数列是满足如下性质的一个数列：
$F_n = \left\{\begin{aligned} 1 \space (n \le 2) \\ F_{n-1}+F_{n-2} \space (n\ge 3) \end{aligned}\right.$
题目描述
请你求出 F_nmod 10⁹ + 7的值。

输入格式
一行一个正整数 n

输出格式
输出一行一个整数表示答案。

输入输出样例
输入：

输出：

详细解析

#include<bits/stdc++.h>
using namespace std;
#define mod 1000000007
typedef long long ll;
const ll N=1e2+7;
ll n;
inline ll read()
{ll a=0;ll f=0;char ch=getchar();while(!isdigit(ch)){f|ch=='-';ch=getchar();}while(isdigit(ch)){a=(a<<3)+(a<<1)+(ch^48);ch=getchar();}return f?-a:a;
}
struct Matrix
{ll a[3][3];Matrix(){memset(a,0,sizeof a);}Matrix operator*(const Matrix &b)const{Matrix res;for(int k=1;k<=2;++k)for(int i=1;i<=2;++i)for(int j=1;j<=2;++j)res.a[i][j]=(res.a[i][j]+a[i][k]*b.a[k][j]%mod)%mod;return res;}
}ans,base;
void init()
{base.a[1][1] = base.a[1][2] = base.a[2][1] = 1;ans.a[1][2] = ans.a[1][1] = 1;
}
void qpow(ll x)
{while(x){if(x&1)ans=ans*base;base=base*base;x>>=1;}
}
int main()
{n=read();if(n<=2) return puts("1"),0;init();qpow(n-2);cout<<ans.a[1][1]%mod;
}