SFM是什么?
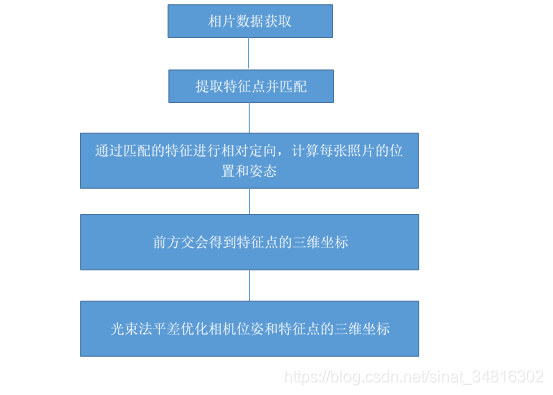
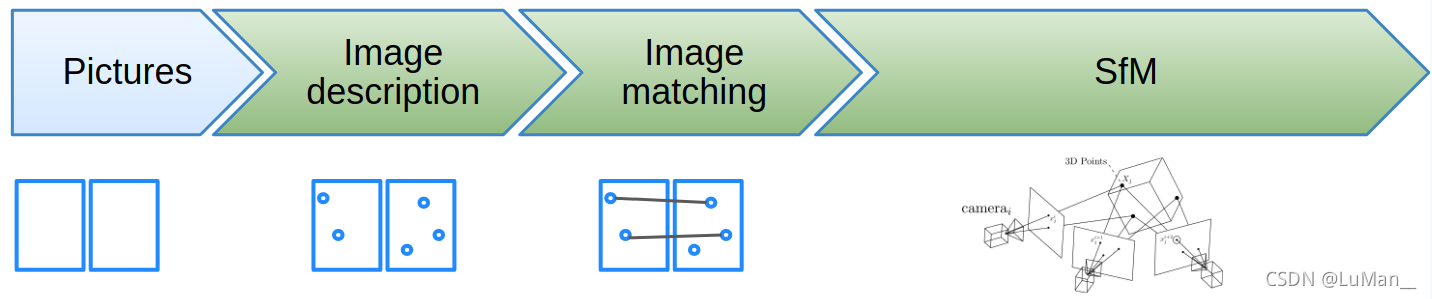
SFM即Structure-from-motion运动结构重建,从大批量图像数据出发,通过相关处理,获取目标图像集3D几何(结构)和摄像机姿态(运动)信息,主要处理流程可分为如下几步:特征提取;特征匹配;姿态估计;束调整。具体处理流程参见下图:
本文主要聚焦于对不同SFM处理方式的梳理总结,对SFM原理部分,可参考该博主的文章:SFM原理简介
总体来说,现有的主流SFM方式可分为如下四类:
全局式SFM
增量式SFM
分层式SFM
混合式SFM
其中后两种处理方式,是近些年来随着三维重建数据量的不断攀升,而逐渐兴起的针对大规模数据处理而诞生的新的处理方式。
全局式SFM
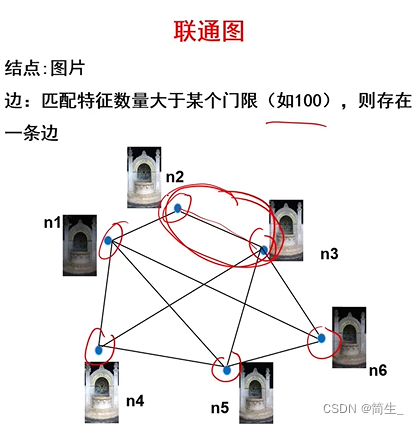
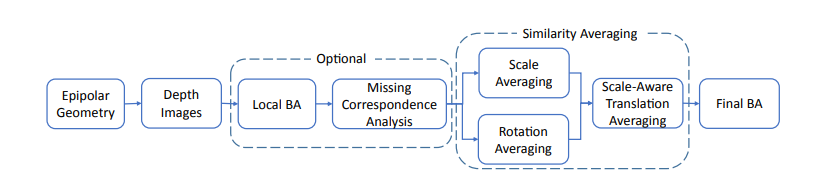
大多数的全局SFM处理可分为如下两步进行。首先,针对场景中的N个视图计算各视图的全局旋转,即旋转平均;然后在该基础上计算各视图的平移,以及结构,即平移平均。而将这两个步骤分开的好处是,即使对于小基线,也可以相当精确地估计相对双视图旋转,而相对平移则不是这样。这些方法考虑了整个极线图,其节点表示视图,并且其中边链接具有足够一致匹配点的视图。图的所有循环都产生多视图约束,也就是说,循环的连续节点中的局部相对运动应该在循环结束时被同一连接。实施这些约束极大地降低了即将介绍的增量方法中所会出现漂移的风险,同时,由于其只需要对数据进行一次全局的BA,因而其对于时间效率的提升也是十分明显的。
但全局式SFM的缺点也是很明显的,由于其是一次性的对所有数据进行处理,因而,其对于噪声特别敏感,如果要使用该处理方式,就必须对数据进行仔细的“过滤”。以去除错误极线信息的影响。
参考文献:
A Global Linear Method for Camera Pose Registration
Global Structure-from-Motion by Similarity Averaging
Linear Global Translation Estimation from Feature Tracks
Shapefit and Shapekick for Robust, Scalable Structure from Motion
Optimizing the Viewing Graph for Structure-from-Motion
Robust Camera Location Estimation by Convex Programming
Robust Global Translations with 1DSfM
Very Large-Scale Global SfM by Distributed Motion Averagin
增量式SFM
增量式SFM基于两个或三个视图的最小重构开始,然后逐渐添加新的视图
,每次添加之后均需要对场景数据进行一次束调整。目前最广泛使用的增量式sfm是ColMap。它执行多个束调整(BA)以使局部结构和运动刚性化。因此,这是一个相当缓慢的过程。由于在处理过程中,每添加一张影像就需要对数据做一次束调整,因而其时间规模是非常恐怖的,但也正由于这一点的存在,使得该种处理方式非常的稳健。
然而,已知增量方法由于误差的累积和难以处理相机轨迹的循环闭合而存在很致命的漂移危险。同时,增量式SFM重建的质量很大程度上取决于初始图像对的选择和后续图像添加的顺序。

参考文献:
Adaptive Structure from Motion with a contrario model estimation
Batched Incremental Structure-from-Motion
Modeling the World from Internet Photo Collections
Photo Tourism- Exploring Photo Collections in 3D
Progressive Large-Scale Structure-from-Motion with Orthogonal MSTs
Structure-from-Motion Revisited
Towards linear-time incremental structure from motion
分层式SFM
随着三维处理数据量呈指数式的爆发,对于动辄几万、几十万张的数据量,传统的全局式SFM已经很难满足人们对于数据处理要求,我们迫切的需要寻求一种可以快速进行大批量数据处理的稀疏重建方法,因而分层式SFM应运而生。
该方法的主要思想很简单,就是对传统增量式SFM的改进,针对传统增量式SFM处理速度同数据量呈线性相关的特点,提出了针对大规模数据集分而治之的处理思想,即首先对原数据集进行划分,获得N个相互关联的子图,然后对个子图进行并行的增量式SFM处理(Local SFM),处理完毕后,对各子图进行合并,获取当前数据的最终处理结果。
该方法的优点是显而易见的,即提升了大规模数据的处理效率,但,另一方面,该方法也存在很多缺点,首当其冲的便是不够稳健,目前大多数的算法都是在子图重建成功的假设上进行后续处理的,没有考虑,一旦处理失败,应该如何处理,同时,必须仔细的考虑图割算法的选择,因为此方法,直接关系着后续局部SFM的重建成功与否;最后子图合并过程中,锚节点的选择也是十分重要的,如果选择错误,很容易出现漂移危险。
参考文献:
Efficient large-scale structure from motion using graph partitioning
Improving the efficiency of hierarchical structure-and-motion.
Structure-and-motion pipeline on a hierarchical cluster tree.
Hierarchical structure-and-motion recovery from uncalibrated images.
混合式SFM
混合式SFM,顾名思义,该处理方式结合了上述处理方式的优点所提出的,该方法处理流程大致如下:
实现进行子图分割,获得N组相互关联的子图,之后对各子图分别采用增量式或者全局式sfm处理,获取其全局旋转信息,然后不进行BA,直接进行后续步骤,使用全局式或者增量式SFM对上一步所获得信息进行处理,获取影像的全局平移信息。
坦率地讲,本人对该方法的研究很浅,因而,对其优缺点的表述也不是十分深刻,因而略过。
参考文献:
HSfM Hybrid Structure-from-Motion.
Parallel Structure from Motion from Local Increment to Global Averaging
Multistage SFM: A Coarse-to-Fine Approach for 3D Reconstructio
欢迎补充!