论文阅读笔记，论文链接

Generative Adversarial Network 生成对抗网络 GAN 理解gan的原理

网络思想

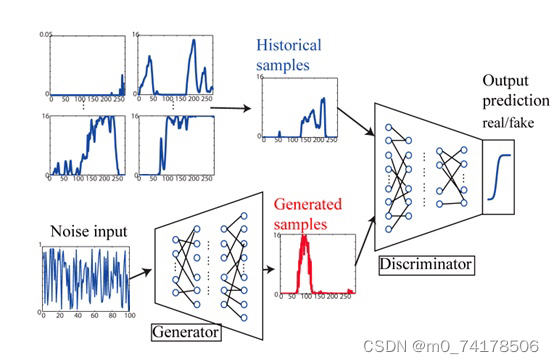
  在GAN网络当中，有两个网络，一个是生成网络G，另外一个是判别网络D。生成网络G的目的是生成数据，这里的数据可以是图片等数据形式。鉴别网络的目的是鉴别输入的数据是真实的数据还是由我们的生成网络生成的数据。对于生成网络，其输入就是一个噪声，输出一个我们想要的逼真的数据（假如说数据是熊猫图像的话，那么输入一个噪声，输出的是熊猫图片，并且这个熊猫图片在我们的判别网络中判别不出来是生成的）。对于鉴别网络，其输入就是数据（真实的数据或者由生成网络生成的数据），输出的就是对这张图片的判别结果，是真实的数据还是由生成网络生成的数据。

  整个网络训练的流程就是，首先固定生成网络的参数（最开始生成网络的参数可以随机初始化），然后使用生成网络生成一堆数据，这堆数据我们将其标签为生成的数据（0为假，1为真）。接着将这堆生成的数据与原始数据混合在一起，去训练我们的鉴别网络。当此次训练完成之后，接着去训练我们的生成网络。我们可以想到，鉴别网络输出的是输入数据是真实数据的概率，那么对于鉴别网络而言，肯定是想让来自生成网络的数据经过鉴别网络，输出的概率越小越好。对于生成网络而言，它则是想要其输出的数据经过鉴别网络，输出的概率越大越好。那么，在训练生成网络的时候，就是最大化其输出结果在经过鉴别网络后的概率。那么这一轮鉴别网络与生成网络的训练就结束了，接着只需要循环上面的步骤即可（固定生成网络的参数，训练鉴别网络。固定鉴别网络的参数，训练生成网络）。

  如果上面的内容你听懂了，那么恭喜你，你已经明白了GAN网络的核心原理。如果你没有听懂，那么接下来举个栗子~

  假设你是一名学画画的学生，现在老师要求你们不用任何参考资料画出考拉🐨。你当时就懵逼了😕，这什么SB老师，不用任何参考资料画出考拉，关键这玩意儿我也没在现实中见过啊😢，算了硬着头皮上吧，要不然给挂科了就难受了。首先你画了10张考拉的画像（图个稳妥，这张不行用那张，不至于都不像），然后你拿到老师那里去交作业。这个老师也是个奇葩，他说他也没见过考拉，所以他打印了一些考拉的照片，然后把你画的图片拿过来一张一张看（这里假设你画的的图像与老师打印出来的图像除了内容上的不一样，其它方面都是一样的），然后他说你这画的是个啥，一点都不像考拉，回去重画，要不然给你0分。mmp，然后你没办法，你就回去重画了。不过接下来在画的过程中你不是一次性画10张图像然后再去找老师了，你现在是画一张，接着就问老师这张有多大的概率像真的考拉，老师给出了一个概率。接着你又画了一张，又去问老师，老师又给出了一个概率，你发现只要你某次画的考拉老师给出的概率比上一次你画的考拉老师给出的概率大，那么这一次考拉与上一次不同的部分，你就可以认为要是像真的考拉靠近，这一部分该这样画。在经过一定数量的询问之后，你心里知道考拉应该怎么画了，然后你拿着你新画出的考拉图像去老师那里，然后老师看你画的考拉与打印出来的考拉，在看的过程中，老师发现了一些东西，然后老师说，虽然这次有些进步，但是画的考拉与真实的考拉还是有不同，要想拿到满分，那就下去继续画吧。然后为了卷死同学，你下去又接着画了，同样重复上述的步骤，在经过n次之后，你心里想着，小样儿，看这次不拿个满分我倒立洗头。然后你拿着你新画的考拉去找老师，老师这个时候傻眼了，卧槽，毕加索再世啊。老师这个时候已经分不出你画的考拉与打印出来的考拉的区别了，于是你成功地拿到了100分，成为卷王。

  虽然我想举原文中的钞票栗子，不过想了想还是谨言慎行为好。在上面的栗子中，你就是生成网络，老师就是鉴别网络。你从最开始的不会画到最后能够画出老师都不能判断是打印出来的还是你画的。老师从最开始的不认识考拉，到最后能够鉴别出画的考拉和打印的考拉。在这个过程中你们相互促进，共同成就，双向奔赴😌~最开始你拿着10张考拉图像去找老师的过程就是固定生成网络参数，训练鉴别网络的过程。然后你每画一张就问一下老师这张像真的可能性有多大，这个过程就是固定鉴别网络参数，训练生成网络的过程（你的每一次询问就是在训练你自己，当概率增大的时候，你觉得你刚才这样画是对的，当概率减小的时候你认为刚才这样画不对）。而上述步骤重复直到最终连老师都不能分辨你画的是真的还是假的，这个时候双方都得到最大的提升。

目标(损失)函数

  在结束了上面的理解之后，我们现在理解一下原文中提出来的目标函数，如下图：

  在理解公式之前，我们先对公式里的几个符号做一个解释：

• D(x):表示的是，对于鉴别网络，输入的是真实的数据x，输出的是该数据是真实数据的概率
• G(Z):表示的是，对于生成网络，输入噪声Z，输出生成的数据
• D(G(Z)):表示的是，对于鉴别网络，输入生成的数据，输出的是该数据是真实数据的概率
• $x\sim P_{data}(x)$:表示的是，真实数据服从的分布
• $z\sim P_z(z)$:表示的是，噪声数据服从的分布

  在理解了GAN的原理之后，我们再来看这个目标函数就会发现很容易理解了。对于里面的max，首先是固定生成网络的参数，将鉴别网络的参数当做我们需要训练的，所以max下面有个D，说明D里的是变量。接着固定鉴别网络的参数，将生成网络的参数当做我们需要训练的，所以min下面有个G，说明G里的是变量。上面的目标函数可以从下面这几个角度来解读：

• 对于鉴别网络而言，我们希望最大化真实数据的概率，而最小化来自生成数据的概率，而最小化来自生成数据的概率相当于最小化$1-D(G(z))$
• 对于生成网络而言，我们希望最大化来自生成数据的概率，而最大化来自生成数据的概率相当于最小化$1-D(G(Z))$

KL散度

  在信息论当中，我们用一件事情发生的概率的负对数表示信息量，如下面的公式(1)所示。也就是事情发生的概率越大，其包含的信息就越少。而一件事情发生的概率越小，那么其包含的信息就越大。
$$\begin{array}{r}H(x_i)=-\log p_i\end{array}\text{\hspace{1em}(1)}$$
  信源熵，也是平均自信息量，如公式(2)所示。其表示的是自信息量(也就是上面提到的信息量)的数学期望，表示为概率与其自信息量的乘积然后再求和。除此之外，还有一个交叉熵的概念，这个我们在深度学习中常常会用到，交叉熵其实就是对于一个分布p来说，我们用分布q来对分布p中的信息进行编码，所需要的信息量。所以我们可以对公式(2)进行改造，改造成公式(3)。如果交叉熵越小，说明用分布q来表示分布p所需要的信息量越小，这也就说明q分布接近p分布，如果这里还不能理解可以去看交叉熵与极大似然的关系，这里不做过多阐述。
$$\begin{array}{r}H(X)=-\sum _i^n{p}_i\log p_i\end{array}\text{\hspace{1em}(2)}$$
$$\begin{array}{r}H(p,q)=-\sum _i^n{p}_i\log q_i\end{array}\text{\hspace{1em}(3)}$$
  根据上面对交叉熵的理解，我们可以知道，交叉熵表示用分布q表示分布p所需要的平均信息量。而这里我们提出一个新的概念，叫做相对熵，也就是我们常说的KL散度，描述两个概率分布之间差异的非对称量。其定义就是用理论分布去拟合真实分布时产生的信息损耗。看完定义之后我想我们就能够推倒（推导）出相对熵的公式了，如公式(4)所示。对，没错，相对熵也就等于交叉熵，减去原始的平均信息量得到我们的信息损耗。从公式(4)(5)我们可以看出KL散度的不对称性，也即是$KL(P||Q)\ne KL(Q||P)$。
$$\begin{array}{r}KL(P||Q)=H(P,Q)-H(P)=\sum _i^n{p}_i\log p_i-\sum _i^n{p}_i\log q_i=-\sum _i^n{p}_i\log \frac{q_i}{p_i}\end{array}\text{\hspace{1em}(4)}$$

$$\begin{array}{r}KL(Q||P)=-\sum _i^n{p}_i\log \frac{p_i}{q_i}\end{array}\text{\hspace{1em}(5)}$$

JS散度

  由于KL散度的不对称性，所以这里引入了一个JS散度，也就是Jensen-Shannon散度，JS散度度量了两个概率分布的相似度，基于KL散度的变体，解决了KL散度非对称的问题，一般地，JS散度是对称的，其取值为[0,1]之间，定义如公式(6)所示。
$$\begin{array}{r}JS(P_1||P_2)=\frac{1}{2}KL(P_1||\frac{P_1+P_2}{2})+\frac{1}{2}KL(P_2||\frac{P_1+P_2}{2})\end{array}\text{\hspace{1em}(6)}$$

目标(损失)函数的证明

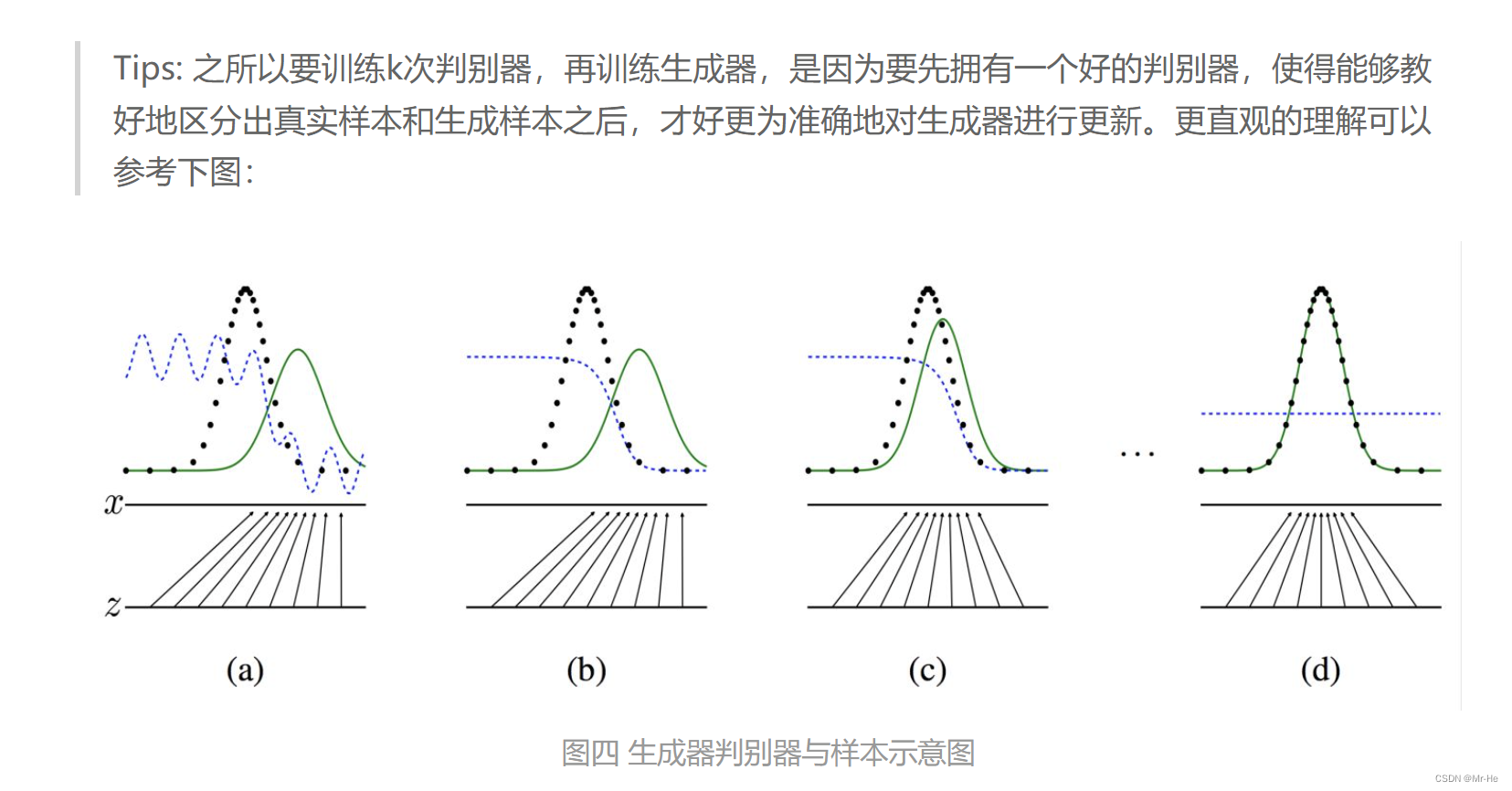
  在了解了上述问题之后，我们回到目标函数。作者提出，这个目标函数的全局最优，存在于生成的数据的概率分布等于真实数据的概率分布。接下来作者给出了数学证明，我们一起来解读一下。首先考虑对于给定的生成器参数，鉴别器什么时候最优。也就是min-max里的max。上面给出的式子是离散情况下的表示，现在我们使用连续情况下的式子表示。下面这个式子也很好理解，第一行就是讲min-max里的max写成积分形式，第二行则是做了一个替换，从$p_z$到$p_g$，其实在生成网络中，利用噪声数据来生成模拟数据，也就是用$p_z$来生成$p_g$，所以等价于第二个积分使用$p_g$做一个替换。
$$\begin{array}{rl}& V(G,D)={\int }_x{p}_{data}(x)\log (D(x))dx+{\int }_z{p}_z(z)\log (1-D(g(z)))dz\\ & ={\int }_x{p}_{data}(x)\log (D(x))+p_g(x)\log (1-D(x))dx\end{array}$$
  那么对于上述的式子我们求解最大值，相当于求解$f(x)=a\log x+b\log (1-x)$的最大值，那么我们求导得$f^{\prime }(x)=\frac{a}{x}-\frac{b}{1-x}=\frac{a(1-x)-bx}{x(1-x)}=\frac{a-(a+b)x}{x(1-x)}$，我们很容易知道当$x=\frac{a}{a+b}$的时候，该函数有最大值。那么对于上述的式子，取得最大值时，鉴别器的分布如下：
$$\begin{array}{r}{D}_G^{\ast }(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\end{array}$$
  现在我们已经求出当生成器的参数固定的时候，鉴别器的最优解。那么现在我们固定鉴别器的参数，来求生成器参数的最优解。首先，将上述求得的值带入式子得。

  接着我们再把上面的式子改写成积分形式，如下。从(1)到(2)也就是对数里，分子分母同时乘以$\frac{1}{2}$，从(2)到(3)，也就是两个对数相加等于对数里的数相乘。从(3)到(4)也就是将积分写开。从(4)到(5)利用的是$p_{data}$与$p_g$的积分为1。从(5)到(6)其实就是套用JS散度公式。那么现在求这个函数的最小值，也就是求JS散度的最小值，而对于JS散度来说，当两个分布相同的时候，也就是$p_{data}=p_g$，那么JS散度取得最小值0。至此，也就证明了该目标函数存在全局最优，也即是当真实的数据分布与生成的数据分布一致的时候达到最优。
$$\begin{array}{rl}& {\int }_x{p}_{data}(x)\log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}dx+{\int }_x{p}_g(x)\log \frac{p_g(x)}{p_{data}(x)+p_g(x)}dx\end{array}\text{\hspace{1em}(1)}$$
$$\begin{array}{rl}& ={\int }_x{p}_{data}(x)\log \frac{\frac{1}{2}{p}_{data}(x)}{\frac{p_{data}(x)+p_g(x)}{2}}dx+{\int }_x{p}_g(x)\log \frac{\frac{1}{2}{p}_g(x)}{\frac{p_{data}(x)+p_g(x)}{2}}dx\end{array}\text{\hspace{1em}(2)}$$
$$\begin{array}{rl}& ={\int }_x{p}_{data}(x)(\log \frac{1}{2}+\log \frac{p_{data}(x)}{\frac{p_{data}(x)+p_g(x)}{2}})dx+{\int }_x{p}_g(x)(\log \frac{1}{2}+\log \frac{p_g(x)}{\frac{p_{data}(x)+p_g(x)}{2}})dx\end{array}\text{\hspace{1em}(3)}$$
$$\begin{array}{rl}& ={\int }_x{p}_{data}(x)\log \frac{1}{2}dx+{\int }_x{p}_{data}(x)\log \frac{p_{data}(x)}{\frac{p_{data}(x)+p_g(x)}{2}}dx+{\int }_x{p}_g(x)\log \frac{1}{2}dx+{\int }_x{p}_g(x)\log \frac{p_g(x)}{\frac{p_{data}(x)+p_g(x)}{2}}dx\end{array}\text{\hspace{1em}(4)}$$
$$\begin{array}{rl}& =2\log \frac{1}{2}+2\times [\frac{1}{2}KL(p_{data}(x)||\frac{p_{data}(x)+p_g(x)}{2})]+2\times [\frac{1}{2}KL(p_g(x)||\frac{p_{data}(x)+p_g(x)}{2})]\end{array}\text{\hspace{1em}(5)}$$
$$\begin{array}{rl}& =-2\log 2+2JSD(p_{data}||p_g(x))\end{array}\text{\hspace{1em}(6)}$$

参考资料

[1] 于风,2020.GAN原理[DB/OL].[2021.11.10].https://www.cnblogs.com/xiaohuiduan/p/13246139.html
[2] Raywit,2020.GAN讲解[DB/OL].[2021.11.10].https://blog.csdn.net/qq_40520596/article/details/1046506909.html
[3] hsinjhao,2019.KL散度介绍及详细公式推导[DB/OL].[2021.11.10].https://hsinjhao.github.io/2019/05/22/KL-DivergenceIntroduction/