状态机与序列机

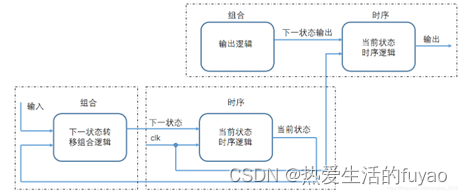
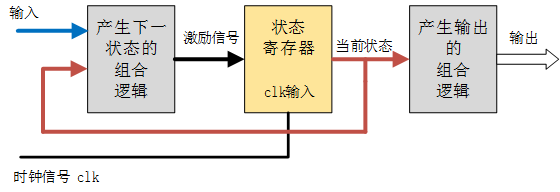
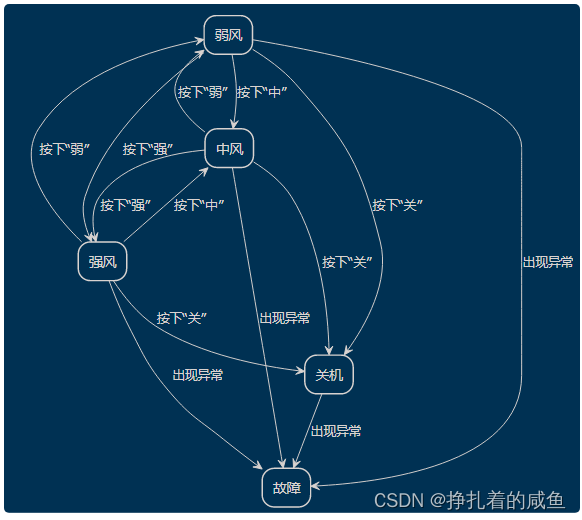
状态机由状态寄存器和组合逻辑电路构成，能够根据控制信号按照预先设定的状态进行状态转移，是协调相关信号动作、完成特定操作的控制中心。

一、线性序列机

序列机是什么：用计数器对时钟个数计数，根据相应时钟周期下的单个周期时间和计数个数可以确定某个时刻的时间，确定时间后再需要时间点转换电平！

采用的是线性序列机其原理就是设计者必须清楚每一个时钟节拍，都有哪些东西发生变化；举个例子：这个东西就好比我们的课表一样，我们第一节上语文课，第二节上数学课，第三节上英语课，它是按照时钟节拍一拍一拍的按照事先已经知道要发生的步骤做着每件事情，而状态机则不同它的灵活性比较高可以随意的从一个状态跳到另一个状态。状态机里面case（state），而序列机里面则是case（count），count表示的是时钟节拍数。

线性序列机的应用：在应用中理解线性序列机

1、ADC驱动实例：

使用一个计数器不断的计数，每个数值对应一个时间，该时间需要进行什么操作就写上去。这样就可以轻松设计出各种时序接口。

TLC5620驱动模块：

module TLC5620_ctrl(clk50M,rst_n,ctrlword,updatareq,updatadone,TLC5620_CLK,TLC5620_DATA,TLC5620_LOAD,TLC5620_LDAC
);input clk50M;input rst_n;input [10:0] ctrlword;input updatareq;output reg updatadone;output reg TLC5620_CLK;output reg TLC5620_DATA;output reg TLC5620_LOAD;output reg TLC5620_LDAC;reg [9:0] counter;/*************************产生计数器************************/always @ (posedge clk50M or negedge rst_n) beginif(!rst_n)counter<=10'd0;else if(updatareq==1|(counter!=10'd0)) beginif(counter==10'd820)counter<=10'd0;elsecounter<=counter+1'b1;endelse counter<=10'd0;end /**********************************************************//*********************线性序列机写接口时序*******************/always @ (posedge clk50M or negedge rst_n) beginif(!rst_n) beginupdatadone<=1'b0;TLC5620_CLK<=1'b0;TLC5620_DATA<=1'b0;TLC5620_LOAD<=1'b0;TLC5620_LDAC<=1'b0;updatadone<=1'b0;endelse begincase(counter)0:beginTLC5620_CLK<=1'b0;TLC5620_DATA<=1'b0;TLC5620_LOAD<=1'b1;TLC5620_LDAC<=1'b0;updatadone<=1'b0;end10:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[10];				end40:TLC5620_CLK<=1'b0;70:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[9];				end100:TLC5620_CLK<=1'b0;130:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[8];				end160:TLC5620_CLK<=1'b0;190:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[7];				end220:TLC5620_CLK<=1'b0;250:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[6];				end280:TLC5620_CLK<=1'b0;310:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[5];				end340:TLC5620_CLK<=1'b0;370:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[4];				end400:TLC5620_CLK<=1'b0;430:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[3];				end460:TLC5620_CLK<=1'b0;490:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[2];				end520:TLC5620_CLK<=1'b0;550:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[1];				end580:TLC5620_CLK<=1'b0;610:beginTLC5620_CLK<=1'b1;TLC5620_DATA<=ctrlword[0];				end640:TLC5620_CLK<=1'b0;670:TLC5620_LOAD<=1'b0;800:TLC5620_LOAD<=1'b1;820:updatadone<=1'b1;default:;endcaseendendendmodule

2、UART发送设计：

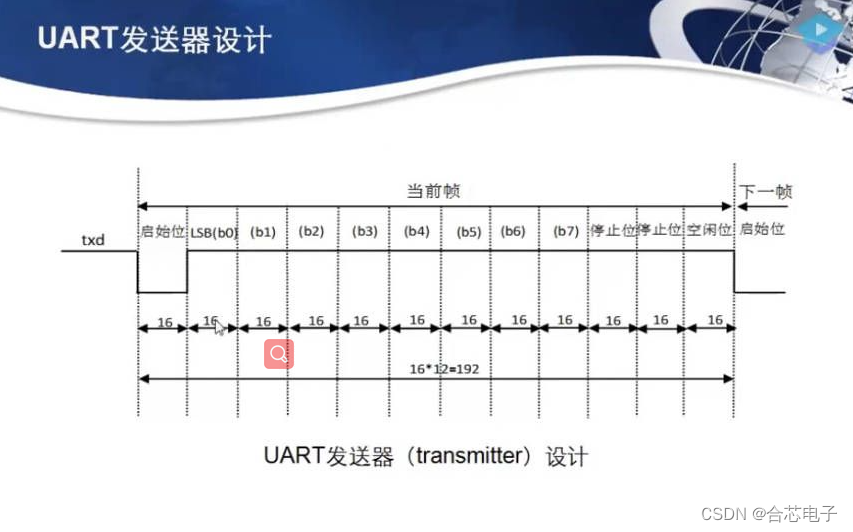
module uart_tx (input			uart_clk,    input			rst_n,  input			tf_empty,input	[7:0]	tf_data,output reg		tf_rdreq,output reg		txd
);reg [7:0] cnt;//节拍计数
reg [7:0] temp_data;//FIFO读数据后进行寄存//LSM_1
always @(posedge uart_clk or negedge rst_n) beginif(rst_n == 1'b0) cnt <= 8'd192;else if (cnt >= 8'd192 && tf_empty == 1'b0) cnt <= 8'd0;eles if(cnt < 8'd192)cnt <= cnt + 1'd1;
end//LSM_2
always @(posedge uart_clk or negedge rst_n) beginif(rst_n == 1'b0) begintxd <= 1'b1;tf_rdreq <= 1'b0;temp_data <= 8'd0;end else case (cnt)0 : begintf_rdreq  <= 1'b0;txd       <= 1'b0;end1 : temp_data <= tf_data;1*16 : txd    <= temp_data[0];2*16 : txd    <= temp_data[1];3*16 : txd    <= temp_data[2];4*16 : txd    <= temp_data[3];5*16 : txd    <= temp_data[4];6*16 : txd    <= temp_data[5];7*16 : txd    <= temp_data[6];8*16 : txd    <= temp_data[7];9*16 : txd    <= 1'b1;endcaseendendmodule

二、有限状态机

1、有限状态机简写为FSM（Finite State Machine），主要分为2大类：

第一类，输出只和状态有关而与输入无关，则称为Moore状态机；

第二类，输出不仅和状态有关而且和输入有关系，则称为Mealy状态机。

Mealy型：输出信号不仅取决于当前状态，还取决于输入；

Moore型：输出信号只取决于当前状态；

实现相同的功能时，Mealy型比Moore型能节省一个状态（大部分情况下能够节省一个触发器资源，其余情况下使用的资源相同，视状态数和状态编码方式决定），Mealy型比Moore型输出超前一个时钟周期。

2、状态机写法

一段式：一个always块，既描述状态转移，又描述状态的输入输出，当前状态用寄存器输出。一段式写法简单，但是不利于维护，状态扩展麻烦，状态复杂时易出错，不推荐；

二段式：两个always块，时序逻辑与组合逻辑分开，一个always块采用同步时序描述状态转移；另一个always块采用组合逻辑判断状态转移条件，描述状态转移规律以及输出，当前状态用组合逻辑输出，可能出现竞争冒险，产生毛刺，而且不利于约束，不利于综合器和布局布线器实现高性能的设计；

三段式：三个always块，一个always模块采用同步时序描述状态转移；一个always采用组合逻辑判断状态转移条件，描述状态转移规律；第三个always块使用同步时序描述状态输出，寄存器输出。

三段式与二段式相比，关键在于根据状态转移规律，在上一状态根据输入条件判断出当前状态的输出，从而在不插入额外时钟节拍的前提下，实现了寄存器输出。

3、状态机序列检测

使用三段式FSM有限状态机进行序列检测，使用摩尔型状态机，最终输出与输入无关。

使用状态机检测“1101”，串行输入的测试序列为“11101101011010”，输出信号为valid有效信号，检测到时输出高，否则为低，考虑序列叠加情况，比如“1101101”，则有两个“1101”，

即：

时钟	1	2	3	4	5	6	7	8	9	10	11	12	13	14	…
输入	1	1	1	0	1	1	0	1	0	1	1	0	1	0	…
输出	0	0	0	0	0	1	0	0	1	0	0	0	0	1	…

11101101011010，在第5个时钟检测到序列，下一个时钟输出高电平；

11101101011010，在第8个时钟检测到序列，下一个时钟输出高电平；

11101101011010，在第13个时钟检测到序列，下一个时钟输出高电平；

根据待检测的序列“1101”确定状态，其中S1为检测到第1个有效位“1”，S2为检测到2个有效位“11”，S3为检测到3个有效位“110”，S4位检测到4个有效位“1101”，IDLE为其他状态；

IDLE：初始状态，除S1~S4外的其他所有状态

S1：1，来1则到S2(11)，否则回到IDLE；

S2：11，来0则到S3(110)，否则保持S2(11)；

S3：110，来1则到S4(1101)，否则回到IDLE；

S4：1101，来1则到S2(11)，否则回到IDLE；

摩尔型，输出和输入无关，S4时无论输入什么，都输出1

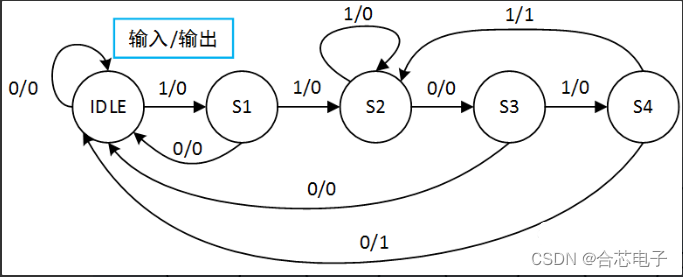
即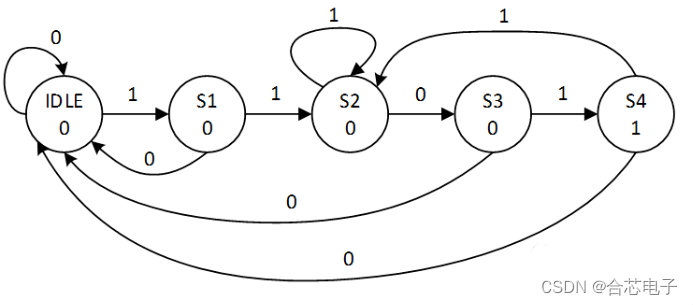

三段式FSM的代码：

module FSM_SequDetection_1(clk,rst_n,data_in,data_valid
);input clk;
input rst_n;
input data_in;
output reg data_valid;//定义状态，这里采用的独热码（One-Hot），FPGA中推荐用独热码和格雷码（Gray）
//状态较少时（4-24个状态）用独热码效果好，状态多时格雷码（状态数大于24）效果好
parameter IDLE = 5'b00001;
parameter S1       = 5'b00010;
parameter S2       = 5'b00100;
parameter S3       = 5'b01000;
parameter S4       = 5'b10000;reg [4:0] current_state;             //现态
reg [4:0] next_state;                 //次态//三段式FSM，第一段，同步时序逻辑，描述状态切换，这里的写法固定
always @ ( posedge clk )
beginif(!rst_n ) begincurrent_state<= IDLE;endelsebegincurrent_state<= next_state;end
end//三段式FSM，第二段，组合逻辑，判断状态转移条件，描述状态转移规律
//这里面用"="赋值和用"<="没区别
always @ (*)
beginif(!rst_n ) beginnext_state<= IDLE;endelsebegincase(current_state )IDLE:    beginif(data_in == 1 )next_state<= S1;elsenext_state<= IDLE;endS1   :      beginif(data_in == 1 )next_state<= S2;elsenext_state<= IDLE;endS2   :      beginif(data_in == 0 )next_state<= S3;elsenext_state<= S2;endS3   :      beginif(data_in == 1 )next_state<= S4;elsenext_state<= IDLE;endS4   :      beginif(data_in == 1 )next_state<= S2;elsenext_state<= IDLE;enddefault   : beginnext_state<= IDLE;endendcaseend
end//三段式FSM，第三段，同步时序逻辑，描述状态输出，摩尔型输出
always @ ( posedge clk )
beginif(!rst_n ) begindata_valid<= 1'b0;endelsebegincase(next_state )S4   : data_valid <= 1'b1;default   : data_valid <= 1'b0;endcaseend
endendmodule

三、总结

线性序列机LSM（Linear Sequential Machine）是比较新的一种自动机模型，也可以说模型的提出并不新（上世纪50年代），但作为高端EDA理论的补充，的确是非常新颖的。

有限状态机（Finite State Machine），在理论体系中，隶属于有限自动机FA的集合，或者说，LSM与FAM的理论体系是相同的。广义的FSM包含LSM，或者说，LSM是广义FSM的特例：状态转移按照线性规律，始终从上一个状态转向唯一的一个下一个状态。

因此，可以这样定义：侠义的FSM：状态转移过程是非线性的，状态的转移具有多个出口（多个分支）LSM：状态的转移过程是线性的，LSM中的任一个状态有且仅有一个出口历史上学术界，并不像现在这样将上述定义用作LSM的定义，而是将后者称为SM（Sequential Machine）。由于大多数复杂控制逻辑中，既有线性转移部分，也有非线性转移部分，所以历史上这种按照FSM理论实现非线性转移，按照SM（或LSM）理论实现线性转移的应用例子很多，学术界称为PLSM（或PSM， Partitioned Sequential Machine）。它（PLSM）线性序列机LSM是更深入的数学模型，是指由节点组成的线性序列过程中，仅有乘加模型，因此其分析方法可以采用线性数学理论。相关研究属于比较前沿的领域。