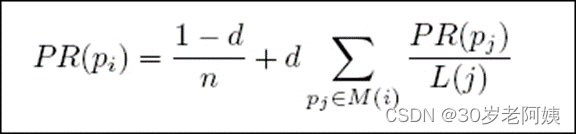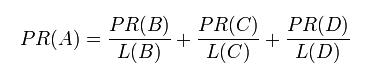PageRank算法到 textRank

1. PageRank算法概述

PageRank,即网页排名，又称网页级别、Google左侧排名或佩奇排名。

是Google创始人拉里·佩奇和谢尔盖·布林于1997年构建早期的搜索系统原型时提出的链接分析算法，自从Google在商业上获得空前的成功后，该算法也成为其他搜索引擎和学术界十分关注的计算模型。目前很多重要的链接分析算法都是在PageRank算法基础上衍生出来的。PageRank是 Google用于用来标识网页的等级/重要性的一种方法，是Google用来衡量一个网站的好坏的唯一标准。在揉合了诸如Title标识和 Keywords标识等所有其它因素之后，Google通过PageRank来调整结果，使那些更具“等级/重要性”的网页在搜索结果中另网站排名获得提升，从而提高搜索结果的相关性和质量。其级别从0到10级，10级为满分。PR值越高说明该网页越受欢迎（越重要）。例如：一个PR值为1的网站表明这个网站不太具有流行度，而PR值为7到10则表明这个网站非常受欢迎（或者说极其重要）。一般PR值达到4，就算是一个不错的网站了。Google把自己的网站的PR值定到10，这说明Google这个网站是非常受欢迎的，也可以说这个网站非常重要。

2. 从入链数量到 PageRank

        在PageRank提出之前，已经有研究者提出利用网页的入链数量来进行链接分析计算，这种入链方法假设一个网页的入链越多，则该网页越重要。早期的很多搜索引擎也采纳了入链数量作为链接分析方法，对于搜索引擎效果提升也有较明显的效果。 PageRank除了考虑到入链数量的影响，还参考了网页质量因素，两者相结合获得了更好的网页重要性评价标准。
对于某个互联网网页A来说，该网页PageRank的计算基于以下两个基本假设：
l    数量假设：在Web图模型中，如果一个页面节点接收到的其他网页指向的入链数量越多，那么这个页面越重要。
l    质量假设：指向页面A的入链质量不同，质量高的页面会通过链接向其他页面传递更多的权重。所以越是质量高的页面指向页面A，则页面A越重要。
       利用以上两个假设，PageRank算法刚开始赋予每个网页相同的重要性得分，通过迭代递归计算来更新每个页面节点的PageRank得分，直到得分稳定为止。 PageRank计算得出的结果是网页的重要性评价，这和用户输入的查询是没有任何关系的，即算法是主题无关的。假设有一个搜索引擎，其相似度计算函数不考虑内容相似因素，完全采用PageRank来进行排序，那么这个搜索引擎的表现是什么样子的呢？这个搜索引擎对于任意不同的查询请求，返回的结果都是相同的，即返回PageRank值最高的页面。

3. PageRank算法原理

PageRank的计算充分利用了两个假设：数量假设和质量假设。步骤如下：
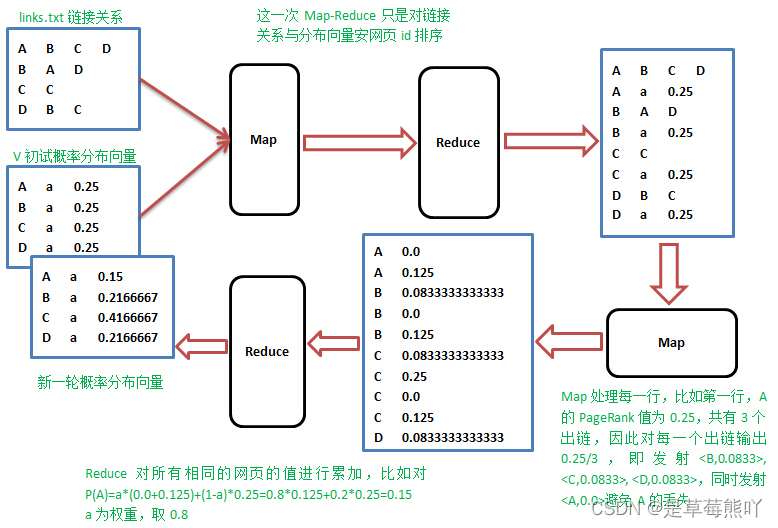
1）在初始阶段：网页通过链接关系构建起Web图，每个页面设置相同的PageRank值，通过若干轮的计算，会得到每个页面所获得的最终PageRank值。随着每一轮的计算进行，网页当前的PageRank值会不断得到更新。

2）在一轮中更新页面PageRank得分的计算方法：在一轮更新页面PageRank得分的计算中，每个页面将其当前的PageRank值平均分配到本页面包含的出链上，这样每个链接即获得了相应的权值。而每个页面将所有指向本页面的入链所传入的权值求和，即可得到新的PageRank得分。当每个页面都获得了更新后的PageRank值，就完成了一轮PageRank计算。

3.2 基本思想：

如果网页T存在一个指向网页A的连接，则表明T的所有者认为A比较重要，从而把T的一部分重要性得分赋予A。这个重要性得分值为：PR（T）/L(T)

　其中PR（T）为T的PageRank值，L(T)为T的出链数

则A的PageRank值为一系列类似于T的页面重要性得分值的累加。

即一个页面的得票数由所有链向它的页面的重要性来决定，到一个页面的超链接相当于对该页投一票。一个页面的PageRank是由所有链向它的页面（链入页面）的重要性经过递归算法得到的。一个有较多链入的页面会有较高的等级，相反如果一个页面没有任何链入页面，那么它没有等级。

3.3 PageRank简单计算：

假设一个由只有4个页面组成的集合：A，B，C和D。如果所有页面都链向A，那么A的PR（PageRank）值将是B，C及D的和。

继续假设B也有链接到C，并且D也有链接到包括A的3个页面。一个页面不能投票2次。所以B给每个页面半票。以同样的逻辑，D投出的票只有三分之一算到了A的PageRank上。

换句话说，根据链出总数平分一个页面的PR值。

例子：

如图1 所示的例子来说明PageRank的具体计算过程。

3.4 修正PageRank计算公式：

由于存在一些出链为0，也就是那些不链接任何其他网页的网，也称为孤立网页，使得很多网页能被访问到。因此需要对 PageRank公式进行修正，即在简单公式的基础上增加了阻尼系数（dampingfactor）q， q一般取值q=0.85。

其意义是，在任意时刻，用户到达某页面后并继续向后浏览的概率。 1-q= 0.15就是用户停止点击，随机跳到新URL的概率）的算法被用到了所有页面上，估算页面可能被上网者放入书签的概率。

最后，即所有这些被换算为一个百分比再乘上一个系数q。由于下面的算法，没有页面的PageRank会是0。所以，Google通过数学系统给了每个页面一个最小值。

这个公式就是.S Brin和 L. Page 在《The Anatomy of aLarge- scale Hypertextual Web Search Engine Computer Networks and ISDN Systems 》定义的公式。

所以一个页面的PageRank是由其他页面的PageRank计算得到。Google不断的重复计算每个页面的PageRank。如果给每个页面一个随机PageRank值（非0），那么经过不断的重复计算，这些页面的PR值会趋向于正常和稳定。这就是搜索引擎使用它的原因。

4. PageRank幂法计算(线性代数应用)

4.1 完整公式：

关于这节内容，可以查阅：谷歌背后的数学

首先求完整的公式：

Arvind Arasu 在《Junghoo Cho Hector Garcia - Molina, Andreas Paepcke, SriramRaghavan. Searching the Web》更加准确的表达为：

是被研究的页面，是链入页面的数量，是链出页面的数量，而N是所有页面的数量。

PageRank值是一个特殊矩阵中的特征向量。这个特征向量为：

R是如下等式的一个解：

如果网页i有指向网页j的一个链接，则

否则＝0。

4.2 使用幂法求PageRank

那我们PageRank 公式可以转换为求解的值，

其中矩阵为 A = q × P + ( 1 一 q) * /N 。 P 为概率转移矩阵，为 n 维的全 1 行. 则 =

幂法计算过程如下：
X 设任意一个初始向量, 即设置初始每个网页的 PageRank值均。一般为1.

R = AX;

while (1 )(

if ( l X - R I < ){ //如果最后两次的结果近似或者相同，返回R

returnR;

} else {

X =R;

R = AX;

}

4.3 求解步骤：

一、 P概率转移矩阵的计算过程:

先建立一个网页间的链接关系的模型,即我们需要合适的数据结构表示页面间的连接关系。

1) 首先我们使用图的形式来表述网页之间关系：

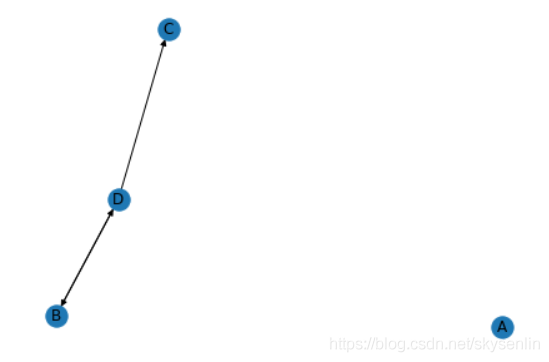
现在假设只有四张网页集合：A、B、C，其抽象结构如下图1：

图1 网页间的链接关系

显然这个图是强连通的（从任一节点出发都可以到达另外任何一个节点）。

2）我们用矩阵表示连通图：

用邻接矩阵 P表示这个图中顶点关系，如果顶（页面）i向顶点（页面）j有链接情况，则pij = 1 ，否则pij = 0 。如图2所示。如果网页文件总数为N ，那么这个网页链接矩阵就是一个N x N 的矩阵。

3）网页链接概率矩阵

然后将每一行除以该行非零数字之和，即（每行非0数之和就是链接网个数）则得到新矩阵P’，如图3所示。这个矩阵记录了每个网页跳转到其他网页的概率，即其中i行j列的值表示用户从页面i 转到页面j的概率。图1 中A页面链向B、C，所以一个用户从A跳转到B、C的概率各为1/2。

4）概率转移矩阵P

采用P’ 的转置矩阵进行计算，也就是上面提到的概率转移矩阵P 。如图4所示：

图2 网页链接矩阵：图3 网页链接概率矩阵：

图4 P’ 的转置矩阵

二、 A矩阵计算过程。

1）P概率转移矩阵 :

2）/N 为：

3）A矩阵为：q × P + ( 1 一 q) * /N = 0.85 × P + 0.15 */N

初始每个网页的 PageRank值均为1 ，即X~t = ( 1 ， 1 ， 1 ) 。

三、循环迭代计算PageRank的过程

第一步：

因为X 与R的差别较大。继续迭代。

第二步：

继续迭代这个过程...

直到最后两次的结果近似或者相同，即R最终收敛，R 约等于X，此时计算停止。最终的R 就是各个页面的 PageRank 值。

用幂法计算PageRank 值总是收敛的，即计算的次数是有限的。

Larry Page和Sergey Brin 两人从理论上证明了不论初始值如何选取，这种算法都保证了网页排名的估计值能收敛到他们的真实值。

由于互联网上网页的数量是巨大的，上面提到的二维矩阵从理论上讲有网页数目平方之多个元素。如果我们假定有十亿个网页，那么这个矩阵就有一百亿亿个元素。这样大的矩阵相乘，计算量是非常大的。Larry Page和Sergey Brin两人利用稀疏矩阵计算的技巧，大大的简化了计算量。

5. PageRank算法优缺点

优点：

是一个与查询无关的静态算法，所有网页的PageRank值通过离线计算获得；有效减少在线查询时的计算量，极大降低了查询响应时间。

缺点：

1）人们的查询具有主题特征，PageRank忽略了主题相关性，导致结果的相关性和主题性降低

2）旧的页面等级会比新页面高。因为即使是非常好的新页面也不会有很多上游链接，除非它是某个站点的子站点。

TextRankPageRank关键词提取算法

本文主要用于实现使用TextRank算法的关键字提取

TextRank是PageRank算法的变种，用于文本关键字关键句的提取

主要参考为原作者Rada Mihalcea论文《TextRank：Bring Order into texts》

整个算法步骤：

【1】文本分词

可以使用常见的java分词，本例使用的是IKAnalyer

【2】词性标注

这个暂时没有实现【只是对提取效果会有一定的影响一般会选择名次和动词作为关键字】不影响算法思想实现

【3】构建初始转置矩阵【图的一种表示方式】

我们以文本对象中的每一个独立文本分词作为一个顶点，采用邻接矩阵来表示文本之间的关联，比如：

“A B C D”

"BC A"

"AC

	A	B	C	D
A	0	0	0	0
B	1	0	0	0
C	1	1	0	0
D	0	0	1	0

(不知道怎么搞的这表格删除不了多余请无视)

words=【A,B,C,D】整个文档的单词数（去重复）

（每个单元格的含义：M[i,j]代表从j->i有指向意即单词words[j] 后面有单词words[i]）

假设上面为3段待提取的文字，分词以空格形式切分，那么我们可以得到下面的一个矩阵M

对上面的矩阵稍作处理使每一列的值结果如下：[有点像单元化处理m[i][j]=m[i][j]/(sum[0-N][j])

	A	B	C	D
A	0	0	0	0
B	1/2	0	0	0
C	1/2	1	0	0
D	0	0	1	0

具体实现：部分源码

[java] view plaincopy

/**
* 传入经过分词处理后的wordsWrapper对象
*matrix[i][j]代表从j->i有指向现在为未带权处理
* @param wordsWrapper
* @return 返回生成的double矩阵
*/
public static double[][] listToGraph(WordsWrapper wordsWrapper) {
int wordCount = wordsWrapper.wordcount;
List<String> nodulWords = Arrays.asList(wordsWrapper.nodulWords);
double[][] a = new double[wordCount][wordCount];
ArrayList<String> content = wordsWrapper.words;
for (String x : content) {
String xs[] = x.split(" ");
int curindex = -1, preindex = -1, nextindex = -1;
for (int i = 0; i < xs.length; i++) {
String tx = xs[i];
int index = nodulWords.indexOf(tx);
if (i != 0) {
preindex = nodulWords.indexOf(xs[i - 1]);
}
if (preindex != -1) {
a[index][preindex] = 1d;
}
}
}
//just for test
// System.out.println("before ...");
//~~~test end here
//初始矩阵处理
for (int j = 0; j < wordCount; j++) {
//这里可以修正为带权值的
int nozero = 0;
for (int i = 0; i < wordCount; i++) {
if (a[i][j] != 0) {
nozero++;
}
}
if (nozero != 0) {
for (int i = 0; i < wordCount; i++) {
a[i][j] = a[i][j] / nozero;
}
}
}
return a;
}

【4】迭代运算

采用最大迭代次数和误差控制判断是否要求迭代

关于每个单词的PR（PageRank）值计算，在论文总是得分计算公式：

其中各个参数含义：

S（Vi）--顶点i的得分可以理解为单词i的PR值

d-----阻尼系数默认为；0.85

In(Vi)---所有指向顶点i的顶点【比如：单词A 面跟着单词B 那么A属于In（B）】

|Out（Vj）|---节点j的出度【与图算法中的出度意义一样上面的是入度】

具体实现：【最大迭代次数(20)和最大容错率由自己指定（0.000001）】

[java] view plaincopy

/**
* 判断是否需要下一次pagerank迭代会进行精度计算和总的迭代次数考虑
*
* @param before 之前迭代结果 PR值
* @param cur当前迭代结果 PR值
* @param curIteration 已经迭代次数
* @return 是否需要下一次迭代
*/
public static boolean neededDoNext(double[] before, double[] cur, int curIteration) {
//先检查迭代次数是否已经超过最大迭代次数
if (curIteration > MAX_ITERATE_NUM) {
return false;
} else {
//精度要求
int n = before.length;
for (int i = 0; i < n; i++) {
if (Math.abs(cur[i] - before[i]) > DEFAULT_ERROR_RATE) {
return true;
}
}
System.out.println("All is ok???");
outputArray(before);
outputArray(cur);
//所有都满足精度要求
return false;
}
}