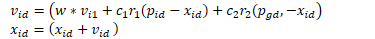0 前言

优化是找到目标函数一组输入的问题，这是机器学习算法的基础，从拟合回归模型到训练人工神经网络，优化算法都是具有挑战性的问题。

流行的优化算法可能有数百种，流行的科学代码库中可能有数十种算法可供选择，这使得从了解到给定优化问题到考虑用哪些算法变得具有挑战性。

1 优化算法

机器学习中最常见的优化问题是连续函数优化，其中函数的输入参数是实数，输出是对输入参数的评估。我们将这种类型的问题称为连续函数优化，以区别于采用离散变量并被称为组合优化问题的函数。

有许多不同类型的优化算法可用于连续函数的优化问题，对优化算法进行分类的一种方法是基于目标函数的可用信息量，而这些信息又可以被优化算法使用和利用。通常，目标函数的可用信息量越多，如果这些信息可以有效地用于搜索，则该函数就越容易优化。

优化算法的主要划分是目标函数是否可以在某一点上微分，即对于给定的候选解，是否可以计算函数的一阶导数（梯度或斜率），这将算法划分为可以利用计算出的梯度信息的算法和不能计算出梯度信息的算法。

可微的目标函数？

• 使用梯度信息的算法
• 不使用梯度信息的算法

下面分别从可微的目标函数和不可微的目标函数进行说明。

2 可微的目标函数

可微函数是可以计算出输入空间中任何给定点的导数的函数。函数某一点的导数是函数在该点的变化率或变化量，通常被称为斜率。
一阶导数： 目标函数在给定点的斜率或变化率。
当导数为0时，该点可能为函数的鞍点或极值点。

多元目标函数的导数是一个向量，向量中的每个元素称为偏导数，或假设所有其他变量保持不变的情况下给定变量在该点的变化率。
如果只想计算函数与某个变量的变化关系时，需要计算偏导数。
偏导数： 多元目标函数的导数。
当函数中某点的所有偏导数都为0时，则该点为函数的极值点或者鞍点。

具有多个输入变量（例如多变量输入）的函数的导数通常称为梯度。
梯度： 多元连续目标函数的所有偏导数构成的向量。

我们可以计算目标函数的导数的导数，即目标函数的变化率的变化率，称为二阶导数。
二阶导数： 目标函数的导数变化的速率。

对于接受多个输入变量的函数，这是一个矩阵，称为Hessian矩阵。
Hessian矩阵： 具有两个或多个输入变量的函数的二阶导数。

简单的可微函数可以使用微积分进行分析优化，如果我们感兴趣的目标函数比较复杂而无法解析求解，此时如果可以计算目标函数的梯度，优化会变得容易很多，因此对使用导数的优化算法的研究要比不使用导数的优化算法要多得多。

使用梯度信息的算法主要包括：

• Bracketing Algorithms
• Local Descent Algorithms
• First-Order Algorithms
• Second-Order Algorithms

2.1 Bracketing Algorithms

Bracketing Algorithms旨在解决具有一个输入变量的优化问题，其中已知最优值存在于特定范围内。

如果没有梯度信息，一些Bracketing Algorithms可以在没有梯度信息的情况下使用。

Bracketing Algorithms原理如下：

Bracketing Algorithms的例子包括：

• 斐波那契搜索
  

• 黄金分割搜索
  

• 二分法
  

2.2 Local Descent Algorithms

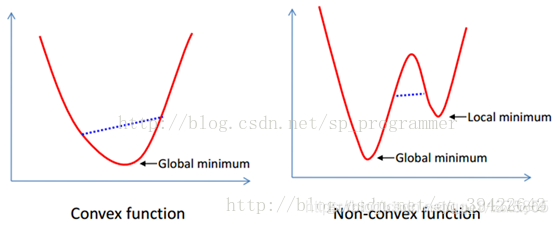
有些算法只能在自己的小范围内搜索极大值或极小值，这些算法称为局部优化算法，常称为经典优化算法。另有些算法，可以在整个超曲面取值范围内搜索最大值或最小值，这些算法称为全局性优化算法，又称为现代优化算法。
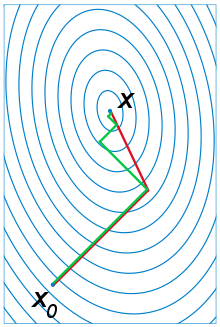
如下图所示，如果自变量 x 是一维的，即一个实数，我们要优化 f(x) ，就只能将 x 向左移动或向右移动，如下图所示。我们希望f(x)最大，就将 x 向使能使f(x)增大的方向移动（左或右）。对于A和B，它们分别向右向左移动，最终到达全局最优点P；而对于C和D，它们只能到达局部最优点Q。所以这些方法称为局部下降优化算法。一般来说，x 是 n 维向量，即x∈ℝn，这样的话，x可以移动的方向就有很多个。n 维情况下，f(x):ℝn→ℝ。

局部下降优化算法（Local Descent Algorithms）旨在解决具有多个输入变量和单个全局最优值（例如单峰目标函数）的优化问题。

局部下降算法最常见的例子是线搜索(line search)算法。

线搜索有许多变体（例如 Brent-Dekker 算法），但该过程通常涉及选择在搜索空间中移动的方向，然后在所选方向的线或超平面中执行包围式搜索。重复此过程，直到无法进行进一步的改进。

summary：
局部下降优化算法是解决无约束优化的一种方法，一般只能得到局部最优解，它的限制是优化搜索空间中的每个方向移动的计算成本很高。

2.3 First-Order Algorithms

一阶优化算法（First-Order Algorithms）使用的是一阶导数（梯度）来选择在搜索空间中移动的方向。

这些过程包括首先计算函数的梯度，然后使用步长（也称为学习率）沿相反方向（例如，下坡到最小化问题的最小值）跟踪梯度。

步长是一个超参数，它控制在搜索空间中移动的距离，这与对每个方向移动执行全线搜索的“局部下降算法”不同。

典型的流程如下（计算当前参数下的梯度，沿负梯度方向更新参数）：

但一阶算法有个缺点，由于梯度越大更新步长越大，导致在峡谷类型的函数上收敛非常慢，会一直在比较陡的方向来回振荡。如下图：

因此，步长太小会导致搜索需要很长时间并且可能会卡住，而步长太大会导致搜索空间出现锯齿形或弹跳，完全错过最优值。

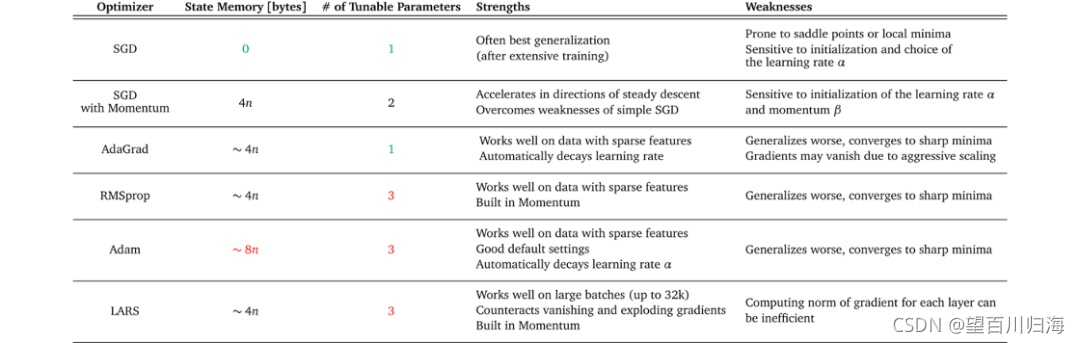
一阶算法通常被称为梯度下降，包括：

• Gradient Descent
• Momentum
• Adagrad
• RMSProp
• Adam

梯度下降算法还衍生了一个新的算法，称为随机梯度下降算法 (SGD)，用于训练人工神经网络（深度学习）模型。

重要的区别在于随机梯度下降算法 (SGD)对内存的要求更小，它使用训练数据的预测误差，因此衍生出三个算法，例如一个样本（随机）、所有样本（批处理）或训练数据的一小部分样本（小批量），如下所示。

• Stochastic Gradient Descent
• Batch Gradient Descent
• Mini-Batch Gradient Descent

2.4 Second-Order Algorithms

二阶优化算法（Second-Order Algorithms）是使用二阶导数（Hessian）来选择在搜索空间中移动的方向。

这些算法仅适用于可以计算或近似 Hessian 矩阵的目标函数。

单变量目标函数的二阶优化算法包括：

• Newton’s Method
• Secant Method

多元目标函数的二阶方法称为拟牛顿法。

• Quasi-Newton Method

拟牛顿法方法有很多，它们通常以算法的开发者命名，例如：

• Davidson-Fletcher-Powell
• Broyden-Fletcher-Goldfarb-Shanno (BFGS)
• Limited-memory BFGS (L-BFGS)

summary：
【优点】因为使用了导数的二阶信息，因此其优化方向更加准确，速度也更快
【缺点】使用二阶方法通常需要直接计算或者近似估计Hessian 矩阵，一阶方法一次迭代更新复杂度为O(N)，二阶方法就是O(N*N)，因此参数量巨大。

3 不可微的目标函数

利用目标函数导数的优化算法快速有效。

然而存在无法计算导数的目标函数，通常是因为各种现实原因，该函数很复杂，或者可以在定义域的某些区域计算导数，但不是在整个定义域。

载着，有些优化算法即使能够计算出一阶或二阶导数，但是在某些情形下依然找不到最优值，如下：

• 没有某些功能的分析描述
• 多个全局最优值
• 随机函数评估（例如噪声）
• 不连续的目标函数

解决以上问题需要黑盒优化算法，之所以这样命名是因为它们对目标函数的假设很少或没有（相对于经典方法），黑盒优化算法分类为：

• 直接算法
• 随机算法
• 人口算法

3.1 Direct Algorithms

直接优化算法适用于无法计算导数的目标函数。

算法是确定性过程，通常假设目标函数具有单一全局最优值，例如单峰。

直接搜索方法通常也称为“模式搜索”，因为它们可以使用几何形状或决策导航搜索空间。

梯度信息直接从目标函数的结果中近似（因此得名），该目标函数比较了搜索空间中点的分数之间的相对差异。 然后使用这些直接估计来选择在搜索空间中移动的方向并对最优区域进行三角测量。

直接搜索算法的示例包括：

• Cyclic Coordinate Search
• Powell’s Method
• Hooke-Jeeves Method
• Nelder-Mead Simplex Search

3.2 Stochastic Algorithms

随机优化算法是在搜索过程中利用随机性来搜索无法计算导数的目标函数的算法。

与确定性直接搜索方法不同，随机算法通常涉及更多目标函数的采样，但能够处理具有欺骗性的局部最优解的问题。

随机优化算法包括：

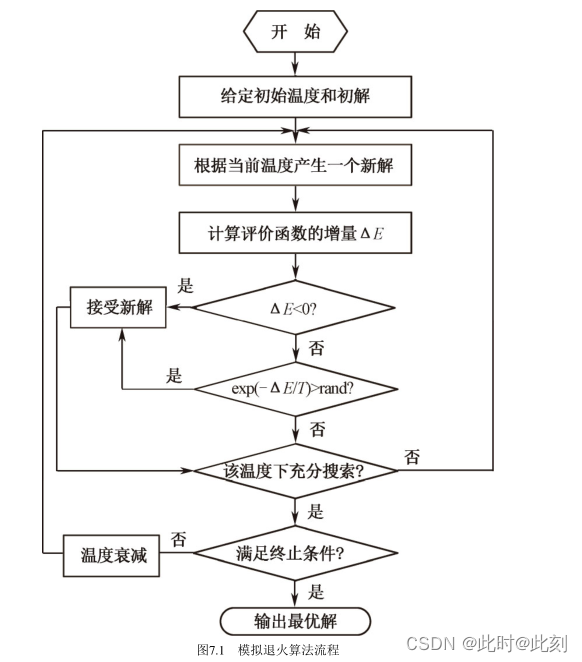
• Simulated Annealing
• Evolution Strategy
• Cross-Entropy Method

3.3 Population Algorithms

种群优化算法是随机优化算法，它维护一个候选解决方案池（种群），这些候选解决方案一起用于采样、探索和磨练最优值。

这种类型的算法旨在解决更具挑战性的客观问题，这些问题可能具有嘈杂的函数评估和许多全局最优（多模态），并且使用其他方法找到一个好的或足够好的解决方案是具有挑战性或不可行的。

候选解决方案池增加了搜索的稳健性，增加了克服局部最优的可能性。

种群优化算法的示例包括：

• Genetic Algorithm
• Differential Evolution
• Particle Swarm Optimization

4 summary

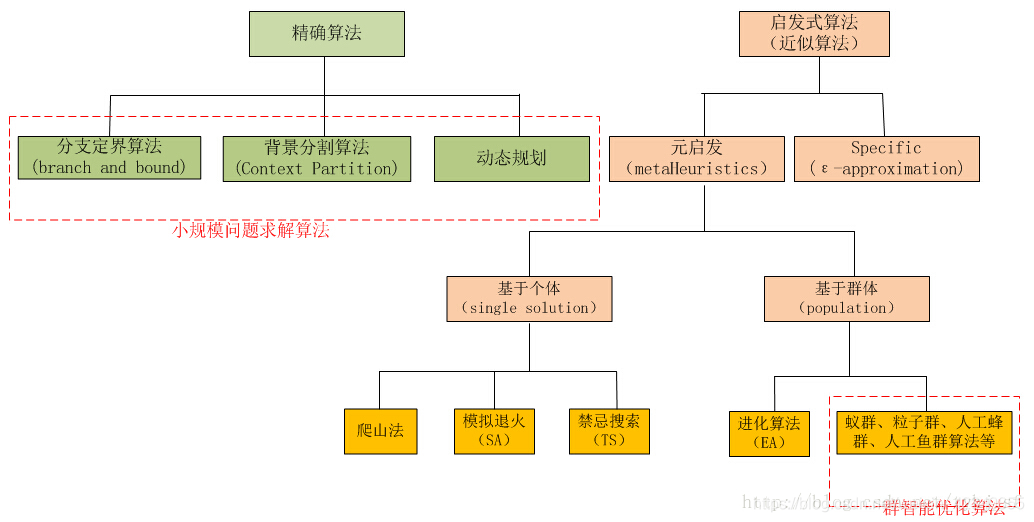
综上，优化算法可以分为使用梯度信息的算法和不使用梯度信息的算法。
经典算法使用目标函数的一阶导数，有时是二阶导数。
而直接搜索和随机算法是为函数导数不可用的目标函数设计的。