5G NR Type II CSI Codebook简介

5G NR Type II Codebook相较于Type I Codebook拥有更高的复杂度和更高的精度。和LTE的Advanced CSI Codebook类似，都有做Linear Combination，但是LTE只从一群Beam Group中挑出两个彼此正交的beam来完成Linear Combination。而5G NR type II CSI Codebook则可以从一群Beam Group中挑选出2/3/4个彼此正交的Beam来完成Linear Combination。另外，除了挑选beam外，每个beam都会有一个对应的幅度和相位调整，幅度调整可以是Wideband与subband同时调整，也可以是Wideband单独调整，但是相位只能由subband调整。因此，更多的beam组合、整合幅度调整和相位调整，使得NR type II CSI Codebook拥有更高的复杂度和精度。

5G NR Type II CSI Codebook的一些基础限制

• 目前NR Type II CSI Codebook的layer数，即rank数最高只支持2。
• Linear Combination支持的Beam的数量为2/3/4，并且彼此正交。
• 幅度调整(Amplitude scaling)可以分为Wideband+Subband或Wideband only。
• 相位调整是在Subband上操作，相位的选择可以为QPSK（2bit）或者8-PSK（3bit）。

简单概述: NR Type II CSI for rank 1 and 2

$\cdot$ PMI Codebook (PMI: Precoder Matrix Index)的两种预编码结构：

1. rank=1
   $$\mathbf{W}=\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{0,0}\\ {\tilde{\mathbf{w}}}_{1,0}\end{array}\right]={\mathbf{W}}_1{\mathbf{W}}_2,\mathbf{W}\text{ is normalized to 1}\text{\hspace{1em}(1)}$$

2. rank=2
   $$\mathbf{W}=\left[\begin{array}{ccc}& {\tilde{\mathbf{w}}}_{0,0}& {\tilde{\mathbf{w}}}_{0,1}\\ & {\tilde{\mathbf{w}}}_{1,0}& {\tilde{\mathbf{w}}}_{1,1}\end{array}\right]={\mathbf{W}}_1{\mathbf{W}}_2,\text{columns of }\mathbf{W}\text{ is normalized to }\frac{1}{\sqrt{2}}\text{\hspace{1em}(2)}$$

$\cdot$ Wighted Linear Combination of several beams

$${\tilde{\mathbf{w}}}_{r,l}=\sum _{i=0}^L{\mathbf{b}}_{k_1^{(i)}{k}_2^{(i)}}\cdot p_{r,l,i}^{WB}\cdot p_{r,l,i}^{SB}\cdot c_{r,l,i}\text{\hspace{1em}(3)}$$

\text{ } \ \ \text{ }     对上式的理解要注意以下几点:

1. beam的数量$L$是可以设置的： L ∈ { 2 , 3 , 4 } L \in \{2,3,4\} L∈{2,3,4}。注意，若令$N_1$为水平方向的双极化天线数，令$N_2$为竖直方向的双极化天线数，那么总的极化天线数为$P_{CSI-RS}=2N_1{N}_2$，$P_{CSI-RS}$与$L$的关系为：
   L = 2 when  P C S I − R S = 4 L ∈ { 2 , 3 , 4 } when  P C S I − R S > 4 (4) \begin{aligned} L=2 &\text{ when } P_{CSI-RS} = 4 \\ L\in\{2,3,4\} &\text{ when } P_{CSI-RS} > 4 \\ \end{aligned} \tag{4} L=2L∈{2,3,4}​ when PCSI−RS​=4 when PCSI−RS​>4​(4)

2. ${\mathbf{b}}_{k_1^{(i)}{k}_2^{(i)}}$是过采样的2D DFT beam。

3. $r=0,1$表示极化方向，$l=0,1$表示第几个layer （rank），要注意区分 $i$ 和 $l$ ，$i$表示第$i$个beam，$l$表示rank。

4. $p_{r,l,i}^{WB}$ : Wideband beam amplitude scaling factor for beam $i$ on polarization $r$ and layer $l$.

5. $p_{r,l,i}^{SB}$: Subband beam amplitude scaling factor for beam $i$ on polarization $r$ and layer $l$.

6. $c_{r,l,i}$: Beam combining coefficient (phase) for beam $i$ on polarization $r$ and layer $l$. 可以设置为QPSK(2 bit)或者8-PSK(3 bit)。

补充一点，式(3)可以看出，$L$个DFT beam与polarization $r$ 无关，与layer $l$ 也无关，选定的beam是什么就用什么，幅度、相位等等再具体做调整。另外，这里我还想强调一点，但这只是我的理解，读者感兴趣的话可以想一想。一般地，矩阵${\mathbf{W}}_1$表示信道的 long-term frequency-independent characteristics，字面上不太好看出来，但是我理解的就是该通信系统所处的信道环境，比如反射、散射物的位置在较长时间内认为不发生变化，那么根据实际的物理环境，我们认为在这较长的时间范围，从发送端打出去的beam，在方向上几乎是保持不变的。

这里给出一个示例，多个beam的线性组合反馈，包括幅度调整（WB Only）和相位调整

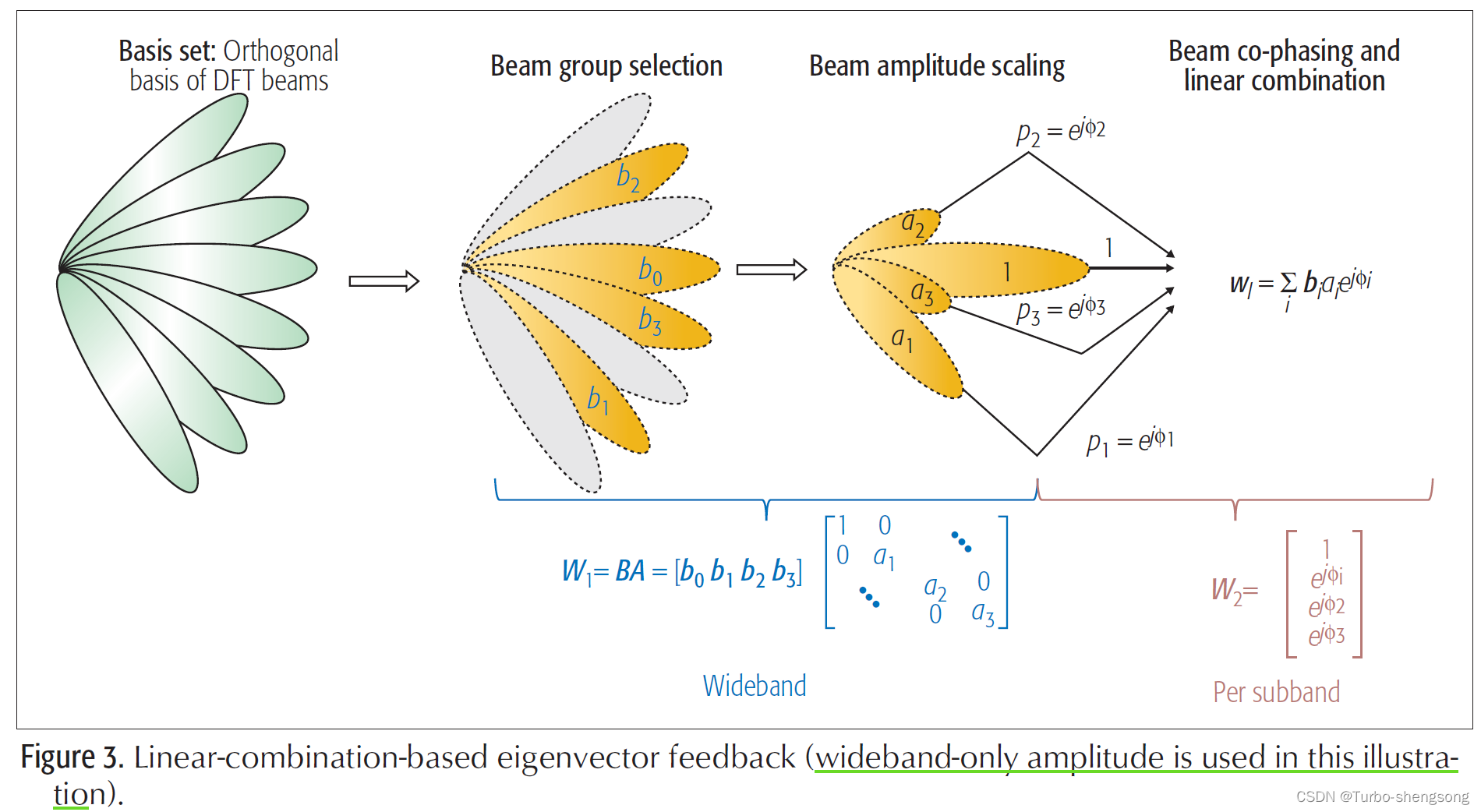
Wideband中的Beam选取(Wideband Only)

这部分我们将说明如何从Beam Group中挑选出 $L$ 个正交的Beam，挑选出来的这些beam的索引由$i_{11}$和$i_{1,2}$决定：

• $i_{11}$: 决定Beam Group中哪些Beam是正交的
• $i_{12}$: 从$i_{11}$所决定的那些彼此正交的Beam中挑选出$L$个

Unconstrained beam selection from the orthogonal basis
我们先给出一个oversampled DFT beam的例子，令$O_1,O_2$分别为水平、竖直方向的过采样数，下图是一个$(N_1,N_2,O_1,O_2)=(2,2,4,4)$的例子

图中黄色的四个方格表示4个正交的beam，$k_1,k_2$分别表示水平和竖直方向上的beam索引（坐标），我们对图中的一些参数做具体的解释

• 水平方向的Beam索引 ($1^{st}$ dimension)
  水平方向的Beam索引我们用$k_i^{(1)}$表征，表示所选取的第$i$个beam的横坐标，具体可写为
  $$k_i^{(1)}=O_1\cdot n_1^{(i)}+q_1,i=0,\cdots ,L-1\text{\hspace{1em}(5)}$$

• 竖直方向的Beam索引 ($2^{nd}$ dimension)
  竖直方向的Beam索引我们用$k_i^{(2)}$表征，表示所选取的第$i$个beam的纵坐标，具体可写为
  $$k_i^{(2)}=O_2\cdot n_2^{(i)}+q_2,i=0,\cdots ,L-1\text{\hspace{1em}(6)}$$

进一步，我们对参数$n_1,n_2$和$q_1,q_2$做具体解释。

首先，我们要明确，当我们确定相关的天线数$N_1,N_2$时，我们实际上就已经可以确定（知道）一组正交的DFT beams，实际上就是图中黄色的4个beam，可以理解为最基本的4个正交beam，这也意味着，我们可以把$n_1^{(i)}.n_2^{(i)}$理解为是基准的正交beam的索引，由 $i_{12}$ 表征，
$$n_1^{(i)}=0,\cdots ,N_1-1;n_2^{(i)}=0,\cdots ,N_2-1.(\text{orthogonal beam indices, }{i}_{12})\text{\hspace{1em}(7)}$$

然后，当我们理解基准正交DFT beams后，我们再来看参数$q_1,q_2$，这两个参数的理解相对比较简单，由上图可以知道，它们所表征的就是基准正交DFT beams的旋转(rotation)，$q_1$表示水平方向beam的旋转，$q_2$表示竖直方向beam的旋转，具体为
$$q_1=0,\cdots ,O_1-1;q_2=0,\cdots O_2-1.(\text{rotation factors},i_{11})\text{\hspace{1em}(8)}$$

这里给出$(N_1,N_2)$和$(O_1,O_2)$的一些参数配置

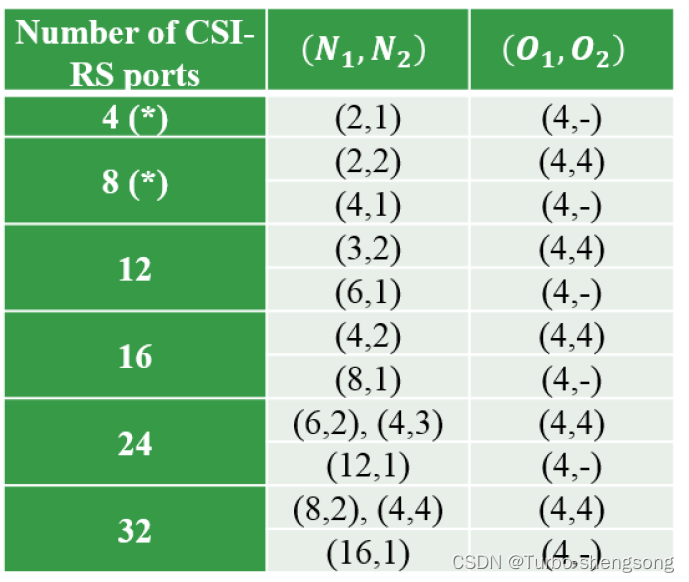
每个Beam的幅度和相位反馈

决定一组正交的Beam之后，我们再来决定每个Beam的幅度和相位，我们分别对幅度调整和相位调整的索引进行说明：

• 幅度调整对应的索引
  (1) Wideband Amplitude: $i_{14}$表征宽带幅度调整的索引，独立于每个Beam、每个Polarization与layer，每个$i_{14}$有8种选择（对应3个bit）。这8种幅度可取的集合为：
  { 1 , 1 2 , 1 4 , 1 8 , 1 1 6 , 1 3 2 , 1 6 4 , 0 } (9) \{1, \frac{1}{\sqrt 2}, \frac{1}{\sqrt 4}, \frac{1}{\sqrt 8}, \frac{1}{\sqrt 16}, \frac{1}{\sqrt 32}, \frac{1}{\sqrt 64}, 0 \} \tag{9} {1,2 ​1​,4 ​1​,8 ​1​,1 ​61​,3 ​21​,6 ​41​,0}(9)

  (2) Subband Amplititude: $i_{22}$表征子带上幅度调整的索引，独立于每个Beam、每个Polarization与layer，每个$i_2$有2种选择（对应1个bit）。这2种幅度可取的集合为：
  { 1 , 1 2 } (10) \{1, \frac{1}{\sqrt 2}\} \tag{10} {1,2 ​1​}(10)

• 相位调整对应的索引
  subband phase: $i_{21}$: 表征子带上相位调整的索引，独立于每个Beam、每个Polarization与layer，可分为8-PSK（3 bit）和QPSK（2 bit）。
  QPSK:  { e j π n 2 , n = 0 , 1 , 2 , 3 } 8-PSK:  { e j π n 4 , n = 0 , 1 , ⋯ , 7 } (11) \begin{aligned} \text{QPSK: } &\{e^{j \frac{\pi n}{2}}, \ n=0,1,2,3\} \\ \text{8-PSK: } & \{ e^{j\frac{\pi n}{4}} , \ n=0,1,\cdots,7 \} \end{aligned} \tag{11} QPSK: 8-PSK: ​{ej2πn​, n=0,1,2,3}{ej4πn​, n=0,1,⋯,7}​(11)

上面所提及的“独立于每个Beam、每个Polarization与layer”是指系统要分别独立地为每个beam $i$，每个polarization $r$， 每个layer $l$ 提供幅度和相位，并且不同的$(r,l,i)$所对应的幅度或相位值都可能不一样，相互之间没有联系。

另外，我们还要补充一个索引
$i_{13}$: 2L个beam中（这里说2L个beam是考虑双极化天线）最强的beam，该beam的所有系数，包括幅度和相位都为1。

幅度和相位调整的比特分配

我们把(Wideband amplitude: $i_{14}$, Subband amplitude: $i_{22}$, Subband phase: $i_{21}$)量化为$(X,Y,Z)$ bits的形式（这里指多少个bit）

• 注意，对每一个 layer，the leading (strongest) coefficient ($i_{13}$)对应于所有$2L$个beams中最强的beam，事实上，对于这个beam，并不需要额外反馈什么，因为我们知道它所对应的系数为1。即
  $$\begin{array}{r}(X,Y,Z)=(0,0,0)\\ \text{ The leading (strongest) coefficient }=1\end{array}$$

• WB+SB amplitude
  $(X,Y)=(3,1)$ and Z ∈ { 2 , 3 } Z \in \{2, 3\} Z∈{2,3} for the first $[\min (K-1,M_l)]$ leading (strongest) coefficients out of $(2L-1)$ coefficients, and $(X,Y,Z)=(3,0,2)$ for the remaining $[2L-\min (K,M_l+1)]$ coefficients.

  其中，$M_l$ is the number of elements of $i_{14}$ that satisfy $i_{14}>0$；
  $K$和$L$的对应关系如下图所示

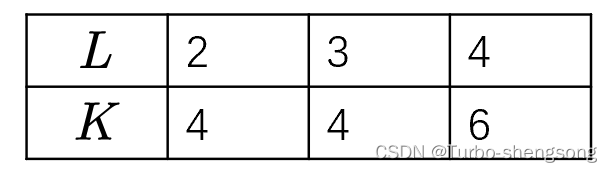
• WB-Only amplitude, i.e. $Y=0$
  ( X , Y ) = ( 3 , 0 ) and  Z ∈ { 2 , 3 } (X,Y) = (3,0) \text{ and } Z \in \{2,3\} (X,Y)=(3,0) and Z∈{2,3}

PMI Indices小结

• 一般认为PMI Codebook具有下面两种结构
  (1) rank=1
  $$\mathbf{W}=\left[\begin{array}{c}{\tilde{\mathbf{w}}}_{0,0}\\ {\tilde{\mathbf{w}}}_{1,0}\end{array}\right]={\mathbf{W}}_1{\mathbf{W}}_2,\mathbf{W}\text{ is normalized to 1}$$

  (2) rank=2
  $$\mathbf{W}=\left[\begin{array}{ccc}& {\tilde{\mathbf{w}}}_{0,0}& {\tilde{\mathbf{w}}}_{0,1}\\ & {\tilde{\mathbf{w}}}_{1,0}& {\tilde{\mathbf{w}}}_{1,1}\end{array}\right]={\mathbf{W}}_1{\mathbf{W}}_2,\text{columns of }\mathbf{W}\text{ is normalized to }\frac{1}{\sqrt{2}}$$

• 上式所描述的分块向量${\tilde{\mathbf{w}}}_{r,l}$可以表示为下面加权线性组合的形式
  $${\tilde{\mathbf{w}}}_{r,l}=\sum _{i=0}^L{\mathbf{b}}_{k_1^{(i)}{k}_2^{(i)}}\cdot p_{r,l,i}^{WB}\cdot p_{r,l,i}^{SB}\cdot c_{r,l,i}\text{wighted combination of L beams}$$

• 索引的描述

上图中，我们可以把$(k_1^{(i)},k_2^{(i)})$理解为是beam的横纵坐标。

Type II Codebook小结

• 使用beam的数量
  • $L=2,3,4$ 对应到(Number of strongest beam K=4,4,6，注意这里有考虑到双极化)
• 幅度调整
  • WB+SB: SB have 2 selections for the strongest $\min (K-1,M_l)$ (1bit) beams, and one selection for the remaining $2L-\min (K,M_l+1)$ beams (0 bit).
  • WB only
    (Note: $W_l$ is the number of elements of $i_{14}$ (Wideband amplitude) that satisfy $i_{14}\ge 0$ )
• 相位调整
  • 8-PSK: for the strongest $\min (K-1,M_l)$ (3bit) beams, and QPSK for the remaining $2L-\min (K,M_l+1)$ beams (2 bit).
  • QPSK
• 支持的layer数
  • #. layer = 1,2

参考

[1] https://www.commresearch.com.tw/Blog/ViewArticle.aspx?guid=28dd1d3f-0f06-4566-8d29-e0e1c9f79c25
[2] http://www.sharetechnote.com/html/5G/5G_CSI_RS_Codebook.html#What_is_Codebook
[3] E. Onggosanusi et al., “Modular and High-Resolution Channel State Information and Beam Management for 5G New Radio,” in IEEE Communications Magazine, vol. 56, no. 3, pp. 48-55, March 2018, doi: 10.1109/MCOM.2018.1700761.