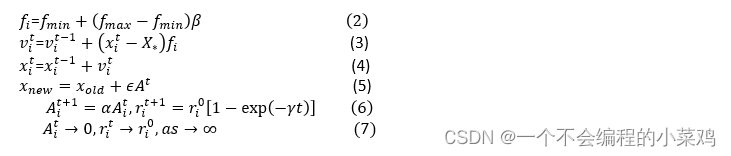大家好，今天和各位分享一下蚁群算法，并基于 tkinter 完成一个旅行商问题。完整代码可以从我的 GitHub 中获得：

https://github.com/LiSir-HIT/Mathematical-Programming/tree/main/Path%20Planning

1. 算法介绍

蚁群算法是由 Mr.Dorigo 博士于 1992 年受蚂蚁寻找食物特性而发明的一种智能仿生算法。蚁群算法用自然语言可以描述为，当蚂蚁在搜索食物时，会在蚁巢和食物源的爬行路径上留下一种化学物质，这种化学物质会引导更多的蚂蚁进行更小路径的食物搜索。蚁群算法常常被用来解决最优化问题。

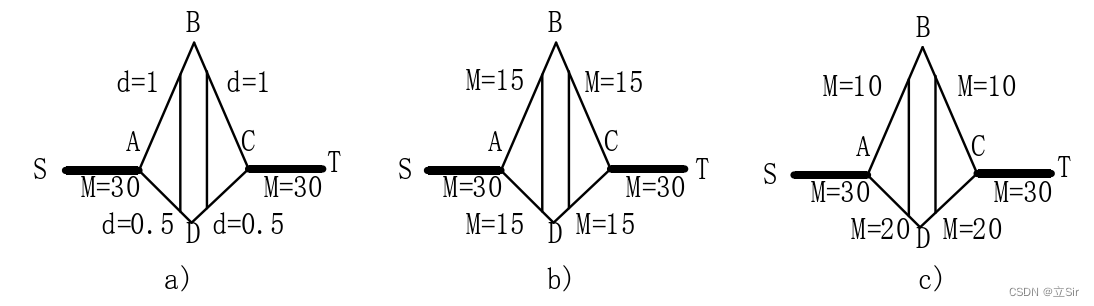
上图分别展示出蚂蚁觅食的三个过程，图中 S 代表蚂蚁的蚁巢（起始点），T 代表蚂蚁要搜寻的食物源（目标点），四边形 ABCD 代表蚁巢到食物源之间的障碍物，其中 AB 与 BC 是长边，边长 d=1，AD 与 DC 是短边，边长 d=0.5。

假设若干只蚂蚁从蚁巢 S 出发去食物源 T 寻找食物，只能经过障碍物边 ABC 或者障碍物边ADC，每只蚂蚁可以产生的信息素为 1，在路径上保留的时间也为 1。在蚂蚁搜寻食物初期，各个边都没有信息素，即信息素初始浓度 $\tau _{ij}(0)=0$ ，若干蚂蚁在起始点 S 去往食物源 T 寻找食物所选路径的概率是相同的，即每条障碍路径上的蚂蚁数量相等，如图 b 所示。

由于路径 ABC 较路径 ADC 更长，所以蚂蚁更倾向于选择路径 ADC 寻找食物源，从而路径 ADC 上所留下的蚂蚁信息素浓度也就更大。这样随着路径 ADC上的浓度越来越大，路径 ABC 上的浓度越来越小，蚂蚁在探寻食物时更倾向于选择路径 ADC，这样就形成一个正反馈，如图 c 所示。随着时间的推移，所有蚂蚁将会全部经过障碍物路径 ADC 由蚁巢到达食物源搬运食物。

2. 蚁群算法原理

在本小节，选用 TSP 问题来说明蚁群算法的原理。根据普遍性规则，某个群体的蚂蚁数量为 m ，将要探索 n 个城市，且同一个蚂蚁不能探索之前已经访问过的城市，城市 i 到城市 j 的距离路径设 $d_{ij}(i,j=1,2,...,n)$ ，某一时刻 t 两城市 i 与 j 之间路径上的信息素浓度设为 $\tau _{ij}(t)$ 。在探索刚开始的时候，每个城市之间路径上的信息素浓度大小相同，设为 $\tau _{ij}(t)=C$

随着搜索时间的推移，各个城市之间路径上的信息素浓度不尽相同，蚂蚁 $k(k=1,2,...,m)$ 将向着信息素浓度高的路径方向上移动，即在 t 时刻蚂蚁 k 由 i 城市移动到 j 城市是依据转移概率 $P_{ij}^k$ 进行的，转移概率的计算公式为：

式中， $\eta _{ij}(t)$ 为启发信息函数，表示城市 i 向城市 j 转移的期望程度，它代表两城市之间距离的倒数，即 $\eta _{ij}(t)=1/d_{ij}(i,j=1,2,...,n)$ ； $allow_k(k=1,2,...,n-1)$ 是 m 只蚂蚁将要探索城市个数的集合。除了蚂蚁的起始城市，集合中共有 n-1个元素，规定蚂蚁 k 不能访问已经探索过的城市； $\alpha$ 为信息素影响因子； $\beta$ 代表启发函数影响因子。

前面提到，蚂蚁在探索路径上所释放的信息素会随着时间的消逝而不断挥发，为表征这种行为，引入全局信息素浓度挥发系数 $\rho (0<\rho<1)$ 。当所有蚂蚁在访问完所有的城市时，即一个循环完成时，需要对路径上的信息素进行全局更新，公式如下：

式中， $\Delta \tau _{ij}$ 表示所有蚂蚁在两城市 (i, j) 之间所释放的信息素浓度的总和，用公式表示如下。

其中 $\Delta \tau _{ij}^k$ 代表信息素浓度的增量。研究者给出三种信息素浓度的计算方法，这三种模型的计算公式如下。

（1）蚂蚁周期系统模型

在蚂蚁周期系统模型中，信息素浓度增量 $\Delta \tau _{ij}^k$ 计算方式如下：

式中，Q 为一个常数，代表蚂蚁经过一个循环后释放的信息素浓度总量； $L_k$ 表示在某次循环中的路径长度。

（2）蚂蚁数量系统模型

在蚂蚁数量系统模型中，信息素浓度增量 $\Delta \tau _{ij}^k$ 计算方法如下：

（3）蚂蚁密度系统模型

在蚂蚁数量系统模型中，信息素浓度增量 $\Delta \tau _{ij}^k$ 计算方法如下：

蚂蚁周期系统模型考虑了全局因素，将蚂蚁所访问城市的路径总长作为整体信息考虑进其中；

蚂蚁数量系统模型只将两个城市间的距离作为影响整个循环过程的信息素浓度，仅仅考虑了局部影响；

蚂蚁密度系统模型更是忽略了各个城市之间的路径距离的因素，只是采取了一个固定的值，来计算释放的信息素浓度。

综上所述，一般采用蚂蚁周期系统模型来计算释放的信息素浓度，由公式可以看到，蚂蚁经历的路径越短，信息素释放浓度越高，更容易达到全局最优。

3. 算法流程

4. 优缺点

4.1 优点

（1）易结合性：该算法可以和很多不同的启发式算法相结合，在结合算法中扬长避短相互弥补算法之间的不足，从而提高算法的收敛速度和精确性。

（2）并行计算能力：该算法是以蚂蚁群体为样本进行的随机搜索算法，拥有群体并行计算的能力。因此常用于大规模问题的求解研究上，可以有效地减少算法的计算时间。

（3）优秀的鲁棒性：蚁群算法优秀的鲁棒性体现在容易与其他算法相结合共同解决研究问题。并且根据不同的研究内容对蚁群算法做出针对性的改进便可以运用在多种研究问题当中。

（4）正反馈机制：蚂蚁会根据路径上信息素浓的度高低，而自适应增减选择该条路径的概率，信息素浓度较高的路径上则会聚集大量蚂蚁，因此每一次迭代中路径上的信息素都会持续增加。初始阶段各条路径的信息素含量较小，在正反馈机制的影响下随着迭代次数的增加较短路径的信息素浓度增长，从而使蚂蚁大量集中在最优解的路径上。

4.2 缺点

（1）极易出现算法的搜索停滞，在算法的随机性作用下不能完全保证蚂蚁在路径选择时找到最短路径。

如果出现蚂蚁大量在局部最优路径上行径，促使该局部最优路径信息素浓度剧增，导致后续大量蚂蚁选择该条路径则会陷入局部最优解的死循环中，不能搜索到全局的最优解。

（2）尽管目前的计算机拥有良好的计算性能和运行速度，但是相对其他启发式算法蚁群算法因自身的复杂程度和并行性会使得算法收敛速度过慢。

尽管蚂蚁通过群体之间的信息交流和适应协作，最终会驱使蚂蚁趋向于行径全局最优解的路径。但算法初期由于信息素的匮乏，道路之间的选择概率差异不大，蚂蚁会根据启发式算法进行选择下一节点，不排除蚂蚁会选择较差路径，这给后续蚂蚁的路径选择造成了误导作用，延缓了搜索到全局最优解的时间。

5. 代码实现

5.1 创建每只蚂蚁对象

每只蚂蚁初始化、搜索路径、选择下一个城市、计算总距离。

class Ant(object):  # 每只蚂蚁的属性def __init__(self, ID):self.ID = ID  # 每只蚂蚁的编号self.__clean_data()  # 初始化出生点#（1）数据初始化def __clean_data(self):self.path = []  # 初始化当前蚂蚁的走过的城市self.total_distance = 0.0  # 当前走过的总距离self.move_count = 0  # 移动次数self.current_city = -1  # 当前停留的城市self.open_table_city = [True for i in range(city_num)]  # 探索城市的状态，True可以探索city_index = random.randint(0,city_num-1)  # 随机初始出生点self.current_city = city_index self.path.append(city_index)  # 保存当前走过的城市self.open_table_city[city_index] = False  # 当前城市以后九不用再次探索了self.move_count = 1  # 初始时的移动计数#（2）选择下一个城市def __choice_next_city(self):# 初始化下一个城市的状态next_city = -1select_citys_probs = [0.0 for i in range(city_num)]  # 保存去下一个城市的概率total_prob = 0.0# 遍历所有城市，判断该城市是否可以探索for i in range(city_num):if self.open_table_city[i] is True:# 获取当前城市(索引)到目标城市i的距离和信息素浓度dis = distance_graph[self.current_city][i]phe = pheromone_graph[self.current_city][i]# 计算移动到该城市的概率select_citys_probs[i] = pow(phe, ALPHA) * pow(1/dis, BETA)# 累计移动到每个城市的概率total_prob += select_citys_probs[i]# 轮盘赌根据概率选择目标城市if total_prob > 0.0:# 生成一个随机数: 0 - 所有城市的概率和temp_prob = random.uniform(0.0, total_prob)# 选择该概率区间内的城市for i in range(city_num):if self.open_table_city[i]:  # 城市i是否可探索temp_prob -= select_citys_probs[i]  # 和每个城市的选择概率相减if temp_prob < 0.0:  # 随机生成的概率在城市i的概率区间内next_city = i  # 确定下一时刻的城市索引break# 如果总概率为0的情况，if next_city == -1:next_city = random.randint(0, city_num-1)  # 随机选择一个城市index# 如果随机选择的城市也被占用了，再随机选一个while(self.open_table_city[next_city] == False):next_city = random.randint(0, city_num-1)return next_city#（3）计算路径总距离def __cal_total_distance(self):temp_distance = 0.0for i in range(1, city_num):# 获取每条路径的起点和终点start, end = self.path[i], self.path[i-1]# 累计每条路径的距离temp_distance += distance_graph[start][end]# 构成闭环end = self.path[0]  # 起点变终点temp_distance += distance_graph[start][end]  # 这里的start是最后一个节点的索引# 走过的总距离self.total_distance = temp_distance#（4）移动def __move(self, next_city):self.path.append(next_city)  # 添加目标城市self.open_table_city[next_city] = False  # 目标城市不可再探索self.total_distance += distance_graph[self.current_city][next_city]  # 当前城市到目标城市的距离self.current_city = next_city  # 更新当前城市self.move_count += 1  # 移动次数#（5）搜索路径def search_path(self):# 状态初始化self.__clean_data()# 搜索路径，遍历完所有城市while self.move_count < city_num:# 选择下一个城市next_city = self.__choice_next_city()# 移动到下一个城市，属性更新self.__move(next_city)# 计算路径总长度self.__cal_total_distance()

5.2 旅行商问题

这部分主要完成绘图和信息素更新


class TSP(object):def __init__(self, root, width=800, height=600, n=city_num):# 创建画布self.width = widthself.height = heightself.n = n  # 城市数目# 画布self.canvas = tkinter.Canvas(root,  # 主窗口width = self.width,height = self.height,bg = "#EBEBEB",  # 白色背景)self.r = 5  # 圆形节点的半径# 显示画布self.canvas.pack()self.new()  # 初始化# 计算两两城市之间的距离，构造距离矩阵for i in range(city_num):for j in range(city_num):# 计算城市i和j之间的距离temp_dis = pow((distance_x[i]-distance_x[j]), 2) + pow((distance_y[i]-distance_y[j]), 2)temp_dis = pow(temp_dis, 0.5)# 距离矩阵向上取整数distance_graph[i][j] = float(int(temp_dis + 0.5))# 初始化def new(self, env=None):self.__running = Falseself.clear()  # 清除信息self.nodes = []  # 节点的坐标self.nodes2 = []  # 节点的对象属性# 遍历所有城市生成节点信息for i in range(len(distance_x)):# 初始化每个节点的坐标x = distance_x[i]y = distance_y[i]self.nodes.append((x,y))# 生成节点信息node = self.canvas.create_oval(x-self.r, y-self.r, x+self.r, y+self.r,  # 左上和右下坐标fill = "#ff0000",      # 填充红色outline = "#000000",   # 轮廓白色tags = "node")# 保存节点的对象self.nodes2.append(node)# 显示每个节点的坐标self.canvas.create_text(x, y-10,text=f'({str(x)}, {str(y)})',fill='black')# 初始化所有城市之间的信息素for i in range(city_num):for j in range(city_num):pheromone_graph[i][j] = 1.0# 蚂蚁初始化self.ants = [Ant(ID) for ID in range(ant_num)]  # 初始化每只蚂蚁的属性self.best_ant = Ant(ID=-1)  # 初始化最优解self.best_ant.total_distance = 1 << 31  # 2147483648self.iter = 1  # 初始化迭代次数# 清除画布def clear(self):for item in self.canvas.find_all():  # 获取画布上所有对象的IDself.canvas.delete(item)  # 删除所有对象# 绘制节点之间的连线def line(self, order):self.canvas.delete('line')  # 删除原线条tags='line'# 直线绘制函数def draw_line(i1, i2):  # 城市节点的索引p1, p2 = self.nodes[i1], self.nodes[i2]self.canvas.create_line(p1, p2, fill='#000000', tags = "line")return i2  # 下一次线段的起点就是本次线段的终点# 按顺序绘制两两节点之间的连线, 为了构成闭环，从最后一个点开始画reduce(draw_line, order, order[-1])# 开始搜索def search_path(self, env=None):self.__running = Truewhile self.__running:# 遍历每只蚂蚁for ant in self.ants:ant.search_path()# 与当前最优蚂蚁比较步行的总距离if ant.total_distance < self.best_ant.total_distance:# 更新最优解self.best_ant = copy.deepcopy(ant)  # 将整个变量内存全部复制一遍，新变量与原变量没有任何关系。# 更新信息素self.__update_pheromone_graph()print(f'iter:{self.iter}, dis:{self.best_ant.total_distance}')# 绘制最佳蚂蚁走过的路径, 每只蚂蚁走过的城市索引self.line(self.best_ant.path)# 更新画布self.canvas.update()self.iter += 1# 更新信息素def __update_pheromone_graph(self):# 初始化蚂蚁在两两城市间的信息素, 50行50列temp_pheromone = [[0.0 for col in range(city_num)] for raw in range(city_num)]# 遍历每只蚂蚁对象for ant in self.ants:for i in range(1, city_num):  # 遍历该蚂蚁经过的每个城市start, end = ant.path[i-1], ant.path[i]# 在两个城市间留下信息素，浓度与总距离成反比temp_pheromone[start][end] += Q / ant.total_distancetemp_pheromone[end][start] = temp_pheromone[start][end]  # 信息素矩阵轴对称# 更新所有城市的信息素for i in range(city_num):for j in range(city_num):# 过去的*衰减系数 + 新的pheromone_graph[i][j] = pheromone_graph[i][j] * RHO + temp_pheromone[i][j]

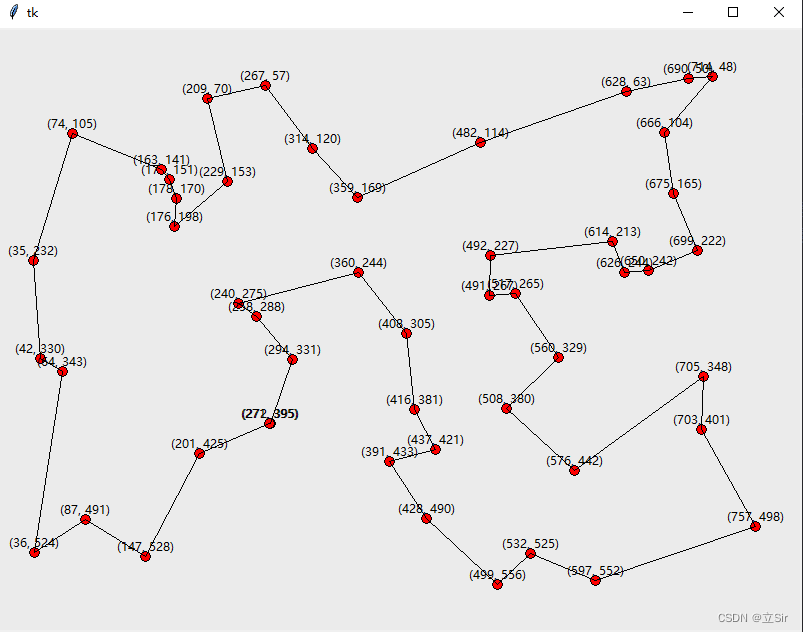
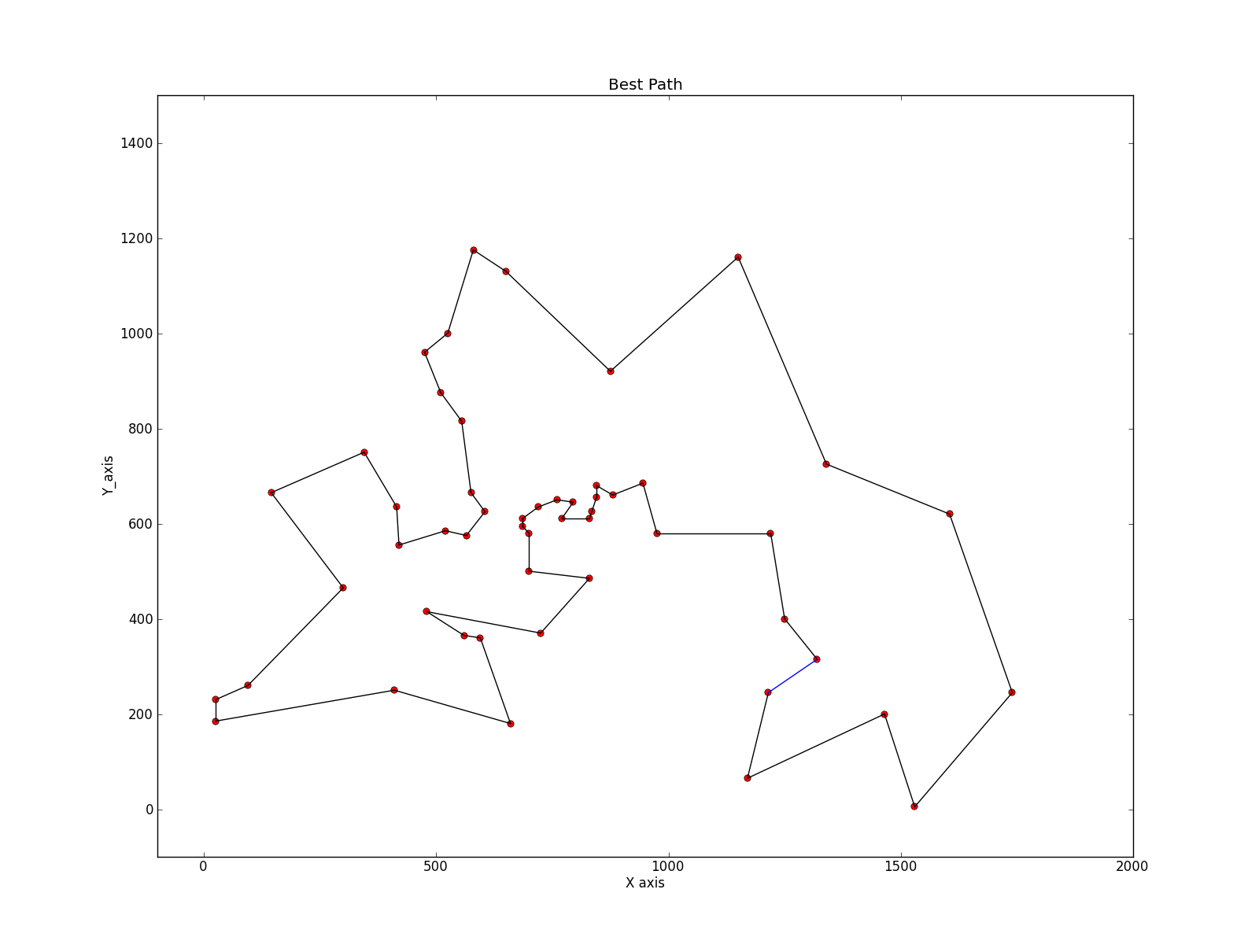
绘制城市选择结果