聚类算法
- 原理
- 步骤
- 代码
- 绘图
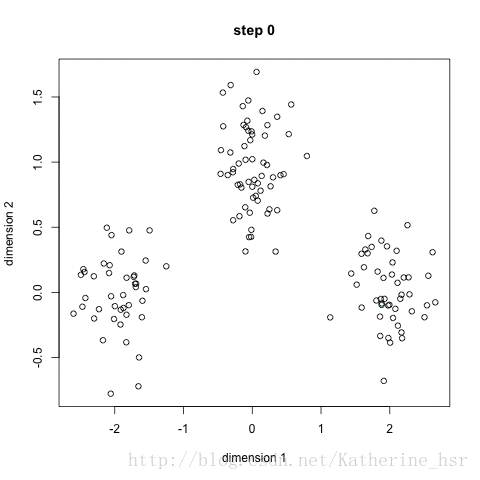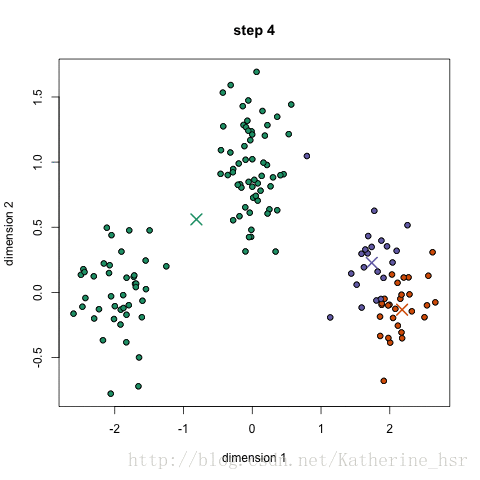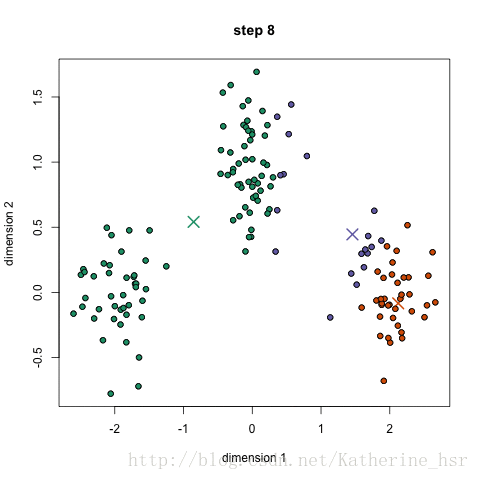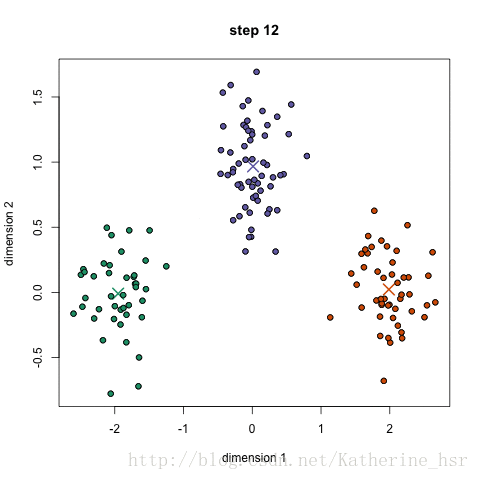
- 选取四个迭代步骤进行可视化(散点图,条形图)
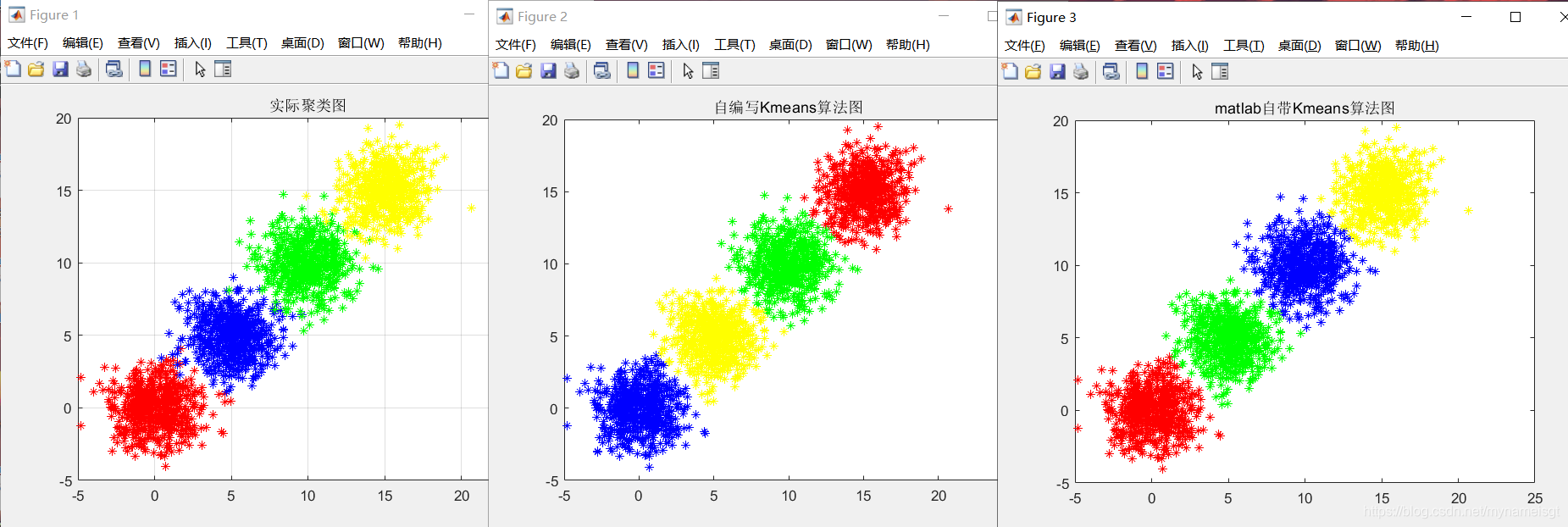
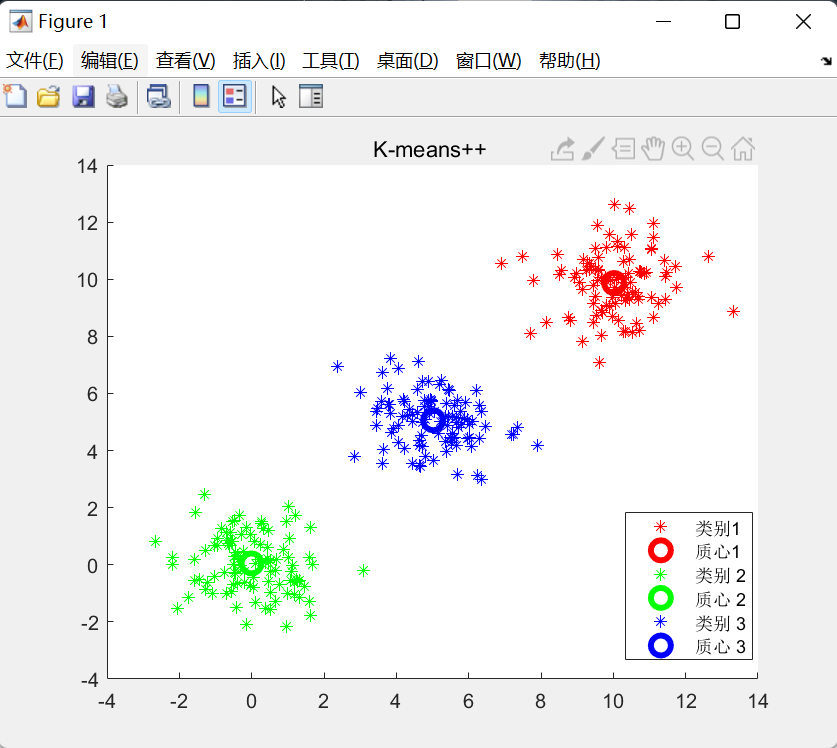
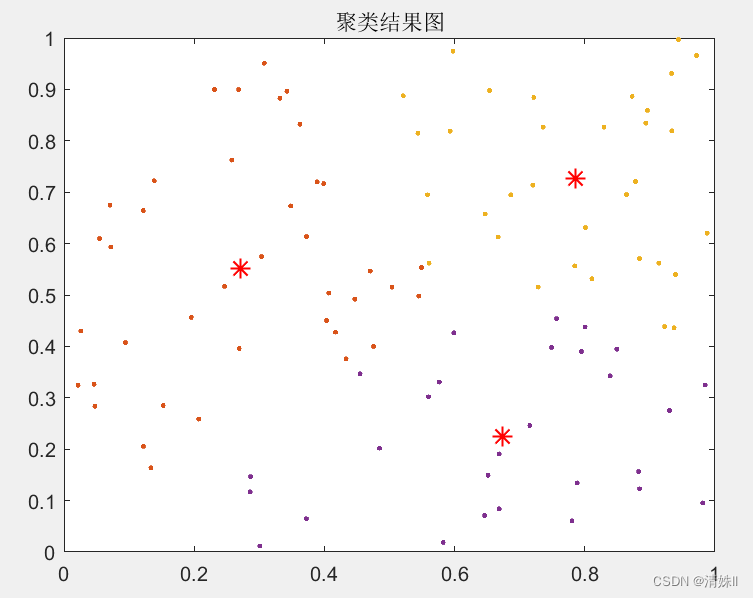
- 聚类结果可视化(散点图)
原理
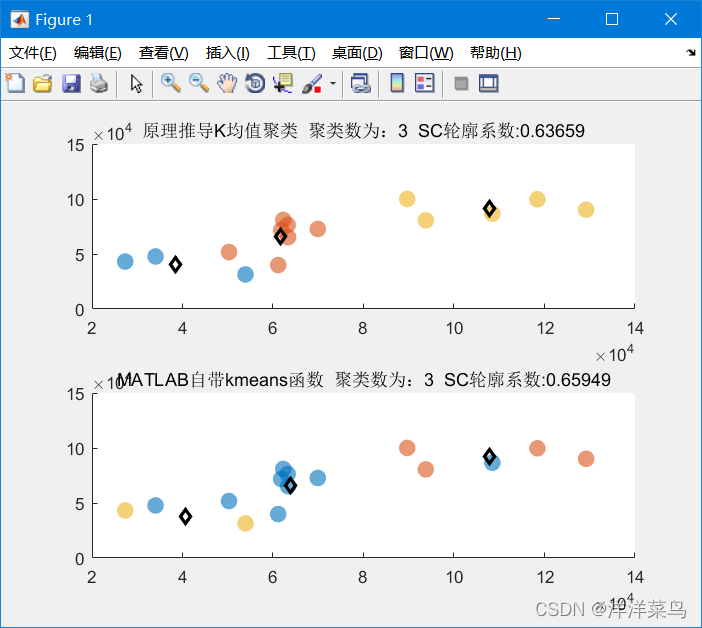
聚类算法的基本思想是:以空间中k个点为中心进行聚类,对距离他们最近的对象进行归类。通过迭代的方法,逐次更新各聚类中心的值,直至得到最好的聚类结果。
步骤
假设要求把样本集分为k个类别:
- 第一步:适当选择k个类的初始中心,一般为随机选取(可利用randperm()函数);
- 第二步:在每次迭代中,对任意一个样本,分别求其到k个中心的距离(一般求欧氏距离),将该样本归到距离最近的中心所在的类;
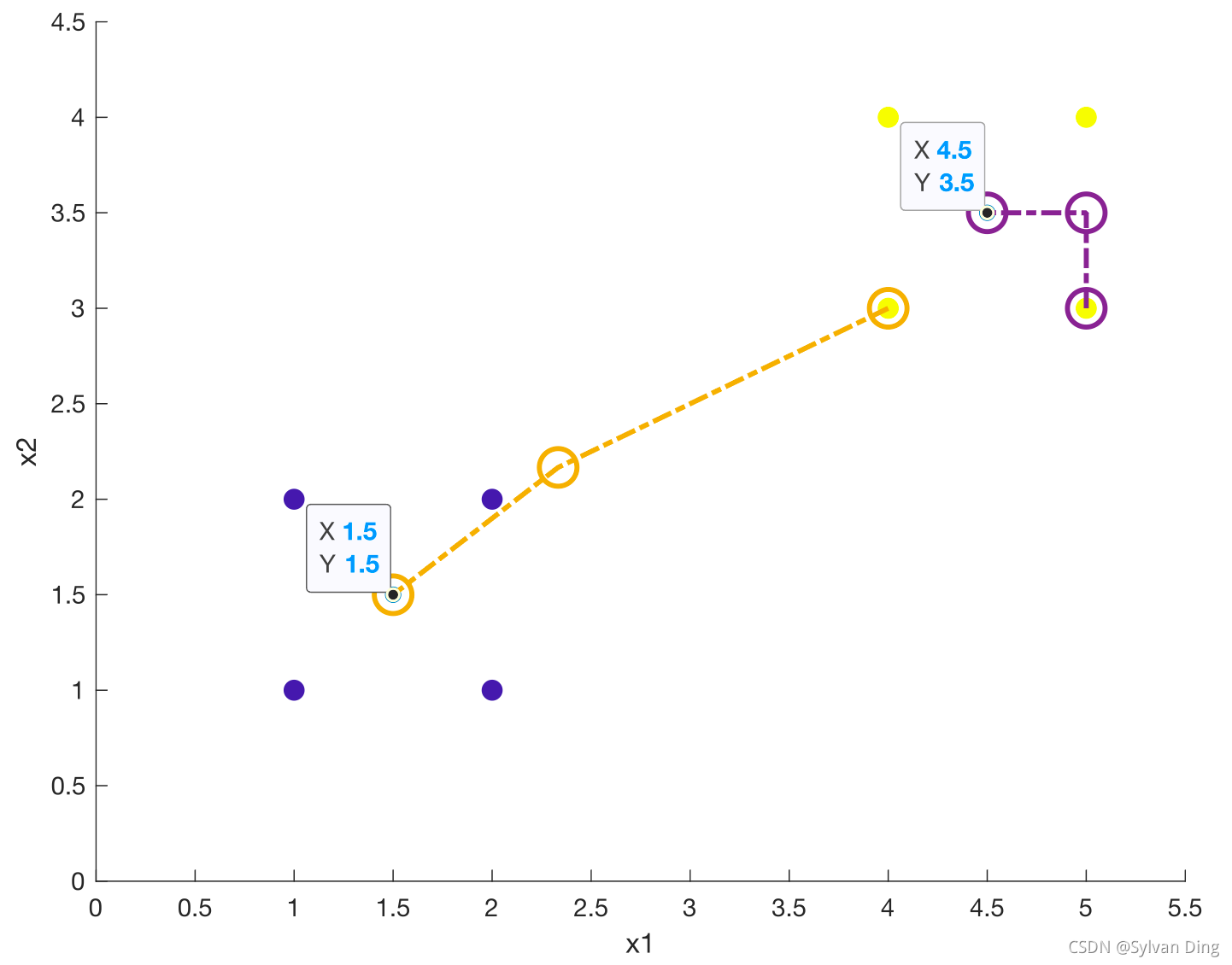
- 第三步:更新k个聚类中心(将聚类中心更新为类中样本点的均值);
- 第四步:设置最大迭代次数,或循环终止条件。对于所有的k个聚类中心,重复第二、三步,当达到最大迭代次数或者聚类中心值的移动距离满足循环终止条件时,则迭代结束,完成分类。
代码
说明:
-
以设置最大迭代次数为例,以便选取四个迭代步骤进行可视化分析
-
假设初始有100个二维样本点(利用rand()函数随机生成)
-
介绍用不同颜色绘出各类样本点的两种方法:
1.利用for循环自动区分颜色
2.使用自定义颜色字符串
% function id=my_k_means(x,k)
k=3;
x=rand(100,2);
n=size(x,1);%记录样本点总个数
%利用randperm()函数随机选取k个点作为初始中心点
c=x(randperm(n,k),:);
y=cell(1,3);
j=1;
step=[1,10,20,30];%选择4个迭代步骤count=zeros(4,k);% 4个迭代步骤中k个不同类中点的个数figure(1)
for iter=1:30%规定迭代次数为30for i=1:k%计算所有样本点分别到k个聚类中心点的距离y{i}=sqrt(sum((x-c(i,:)).^2,2));A=cell2mat(y);[~,id]=min(A,[],2);%求每个样本点到哪个中心距离最小c(i,:)=mean(x(id==i,:));%更新k个中心点分别为属于同类样本点的均值中心endif ismember(iter,step)subplot(2,2,j)plot(c(:,1),c(:,2),'r*','MarkerSize',8,'LineWidth',0.8);title(strcat(num2str(step(j)),'次迭代结果'))hold on%利用for循环完成k类自定义颜色块的绘图colors='bcr';for i=1:k t=x(id==i,:);count(j,i)=size(x(id==i,:),1);plot(t(:,1),t(:,2),"Color",colors(i),"Marker",".","LineStyle","none");hold onendhold offj=j+1; end
end
disp([num2str(k),'个聚类中心分别为:'])
disp(c)
% 绘出样本点以及k个聚类中心
figure(2)
plot(c(:,1),c(:,2),'r*','MarkerSize',10,'LineWidth',1);
hold on;
for i=1:k %!for循环会自动更换颜色z=x(id==i,:);plot(z(:,1),z(:,2),'.');hold on;
end
title('聚类结果图')
hold off
四个迭代步骤的条形图(显示各类点的个数):
figure(3)
b=bar(step,count,'FaceColor','flat');
yticks(0:5:60);
xlabel('迭代次数')
ylabel('不同类点的个数')
for k = 1:size(y,2)b(k).CData = k;
xtips= b(k).XEndPoints;
ytips= b(k).YEndPoints;
labels = string(b(k).YData);
text(xtips,ytips,labels,'HorizontalAlignment','center',...'VerticalAlignment','bottom')
end
绘图
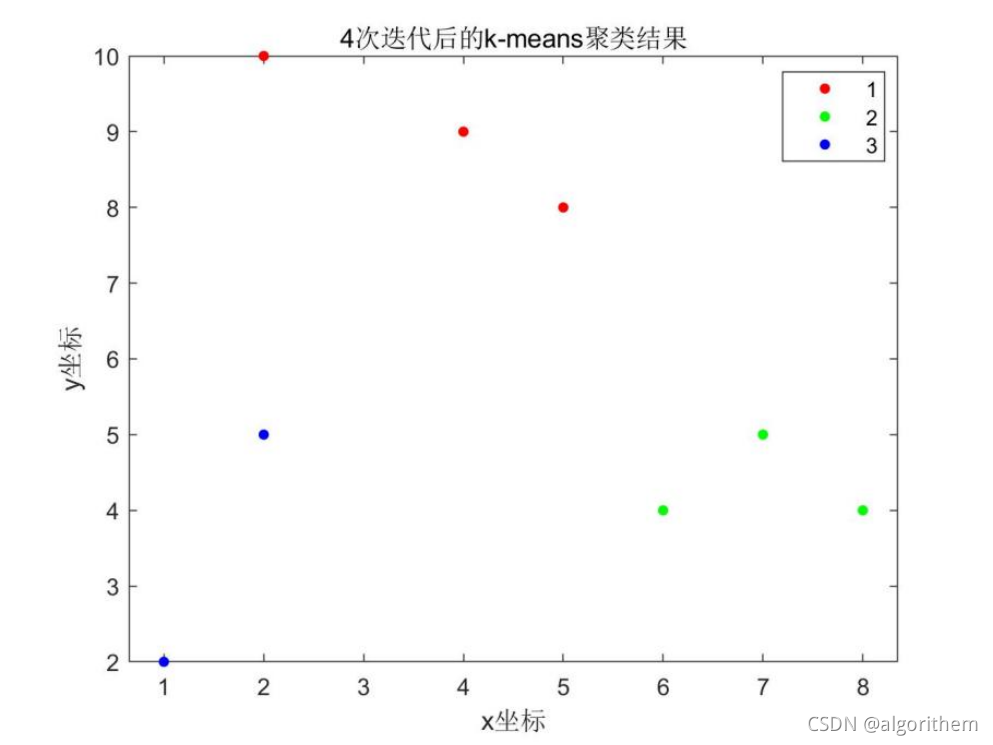
选取四个迭代步骤进行可视化(散点图,条形图)
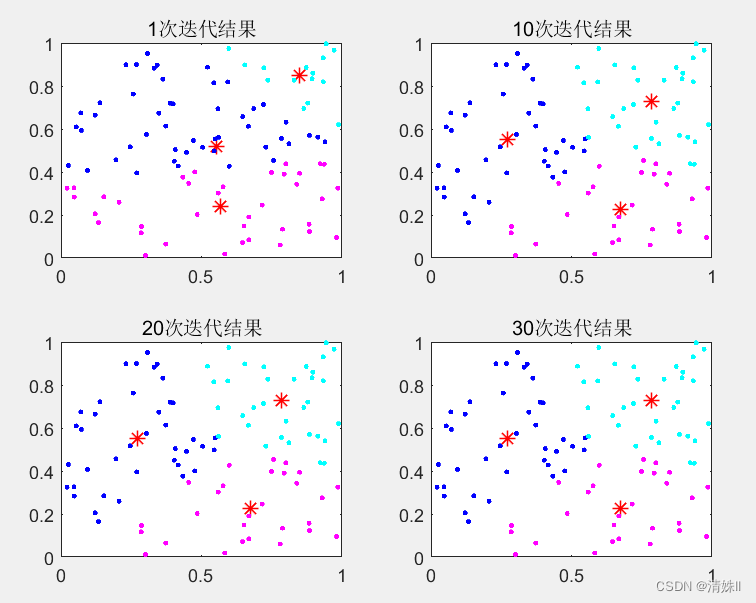
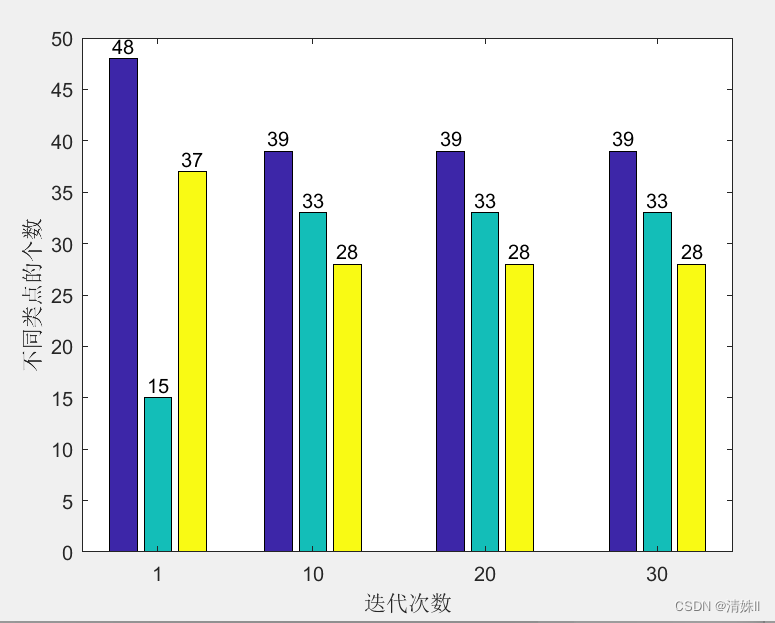
聚类结果可视化(散点图)
结束语:如果有什么不懂的,可以查阅官方文档或留言。
小白写手一枚,参考代码时可根据自我理解改善。