之前讲过用数值积分法(DDA)进行直线逼近,通过向下取整获取目标像素点。计算过程中每一次都需要加0.5这一浮点数,浮点数运算效率相比整数运算效率低的多,因此需要对此进行改进。
一.中点画线法
直线方程式通过一般式表示:,调整A、B参数为整数,且B为正整数。
点在直线上方则,点在直线直线下方则
,点在直线上则
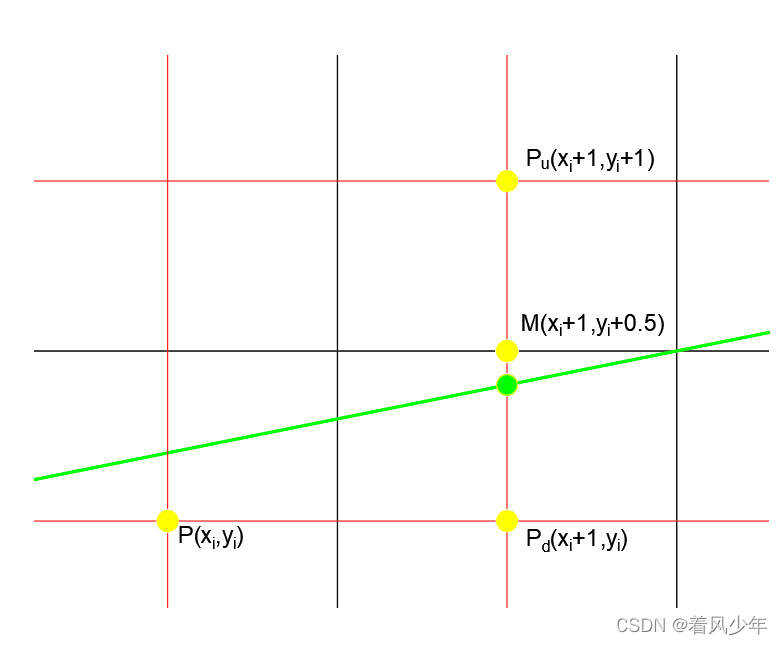
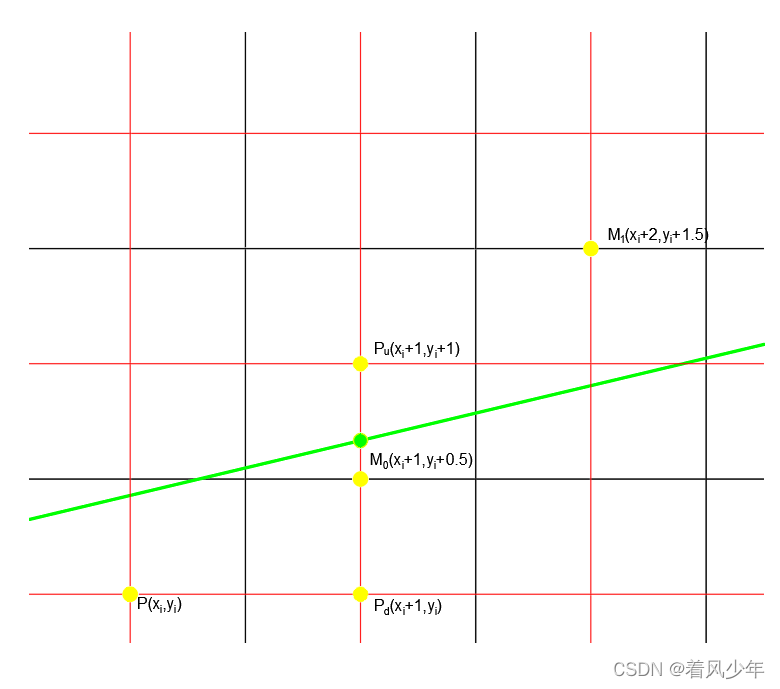
前提条件k∈[0,1],且坐标已经确定。接下来需要判断下一个点是取点
还是取点
。判断的依据是看
和
的中点
位于直线上方还是下方,若位于直线上方则取
点,位于直线下方则取
点,正好位于直线上则任取均可。
由上述可知,d的正负决定下一个像素点是进1还是保持不变。接下来考虑d的递推关系,共分为两种情况。
1.,即中点
位于直线上方,下一个像素点选择为
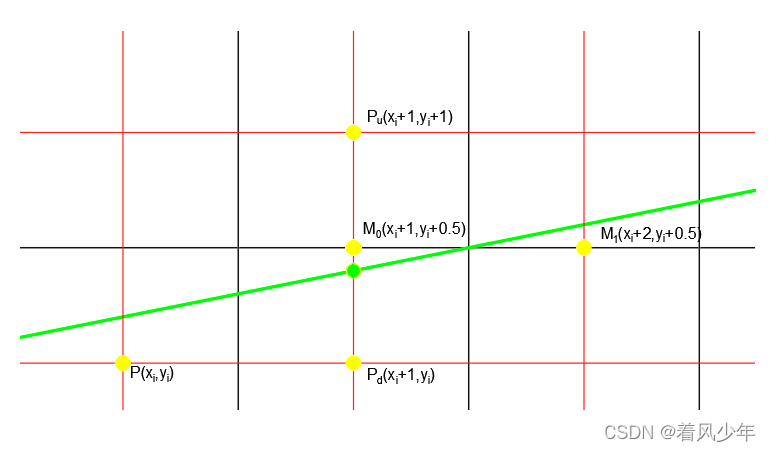
2.,即中点
位于直线下方,下一个像素点选择为
至此,d的增量关系已经确定,最后只需要确定的初值即可。已知P点为线段起点,则初始值
可求。
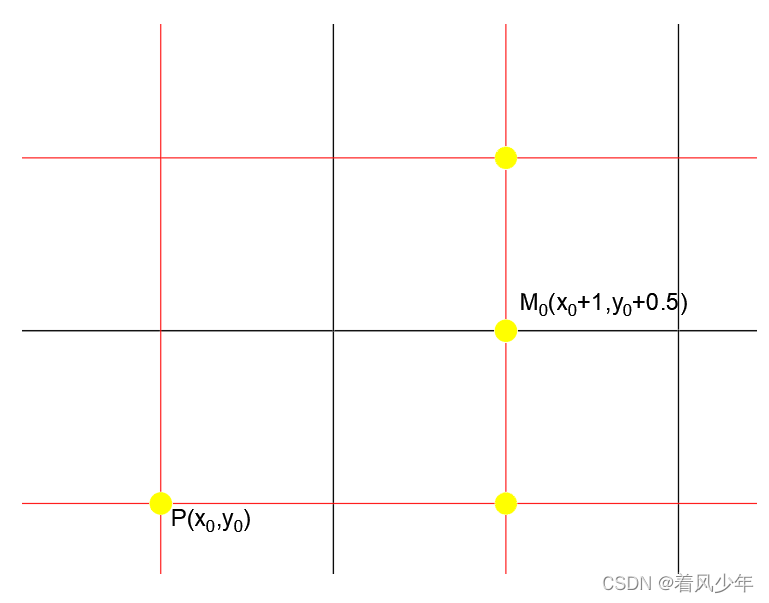
总结:
二.例题推导
已知线段两端点A(0,0)、B(10,8),直线段方程式为
| d | -1.5 | -1 | 0 | -4 | -3 | -2 | -1 | 0 | -4 | -3 | |
| y | 0 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 6 | 7 | 8 |

三.拓展
上述表述中有两个限定条件1.斜率k∈[0,1];2.进给方向为斜向上。若要表述所有的情况,则还需要考虑斜向下进给情况,以及斜率k不为[0,1]的情况。