python cplex优化包教程
在做优化课题时,常常需要用到优化算法。
个人优化算法专栏链接如下:
最优化实战例子
需要掌握一些优化算法,但是一些比较出名的优化工具箱还是要会用。今天讲解下cplex工具箱
CPLEX Optimizer 是一种用于对以下形式的线性优化问题(通常称为线性规划 (LP) 问题)求解的工具


文章目录
- python cplex优化包教程
- 一、安装
- 二、使用步骤
- 1.算例
- 2.求解
- 总结
提示:以下是本篇文章正文内容,下面案例可供参考
一、安装
pip install cplex
二、使用步骤
1.算例
通过下面的一个算例感受下cplex如何求解优化问题
Maximize x1 + 2 x2 + 3 x3 + x4
# Subject to
# - x1 + x2 + x3 + 10 x4 <= 20
# x1 - 3 x2 + x3 <= 30
# x2 - 3.5x4 = 0
# Bounds
# 0 <= x1 <= 40
# 0 <= x2
# 0 <= x3
# 2 <= x4 <= 3
# Integers
# x42.求解
第一步:导入CPLEX的包
import cplex
第二步:初始化一个优化模型
prob = cplex.Cplex() # 此处的prob可以是任意变量名
第三步:设置目标方程的取值方向:求最大值/最小值
prob.objective.set_sense(prob.objective.sense.minimize)
##prob.objective.sense.minimize最小值;
#prob.objective.sense.maximize最大值第四步:添加变量

#4.添加变量
my_obj = [1.0, 2.0, 3.0, 1.0] #目标函数(未知量)系数
my_ub = [40.0, cplex.infinity, cplex.infinity, 3.0] #未知量上限
my_lb = [0.0, 0.0, 0.0, 2.0]#未知量下限
my_ctype = "CCCI"#前面三个实数,x4为整数
my_colnames = ["x1", "x2", "x3", "x4"] #未知量 名称
prob.variables.add(obj=my_obj,lb=my_lb,ub=my_ub,types=my_ctype,names=my_colnames) #
第五步:添加线性约束


lin_expr可以是SparsePair实例的列表,也可以是列表格式的矩阵。lin_expr的表项不能包含重复的索引。如果lin_expr的一个条目通过索引、名称或索引和名称的组合多次引用一个变量,将引发异常。
senses包含线性约束意义的字符串。每个条目必须是’G’、‘L’、'E’和’R’中的一个,分别表示大于或等于(>=)、小于或等于(<=)、相等(=)和排列约束。
RHS是一个浮点数列表,指定每个线性约束的右侧。
Range_values是一个浮点数列表,指定每个线性约束的左侧和右侧之间的差异。如果range_values[i] > 0(0),则约束i被定义为rhs[i] <= rhs[i] + range_values[i]。如果range_values[i] < 0(0),那么约束i被定义为rhs[i] + range_value[i] <= a*x <= rhs[i]。
Names是字符串列表。
#第五步:添加线性约束
my_rhs = [20.0, 30.0, 0.0]
my_rownames = ["r1", "r2", "r3"]
my_sense = "LLE"rows = [[["x1", "x2", "x3", "x4"], [-1.0, 1.0, 1.0, 10.0]],[["x1", "x2", "x3"], [1.0, -3.0, 1.0]],[["x2", "x4"], [1.0, -3.5]]]
prob.linear_constraints.add(lin_expr=rows, senses=my_sense,rhs=my_rhs, names=my_rownames)
第六步:直接调用优化求解器的求解方法(method),一键求解
#第六步:求解
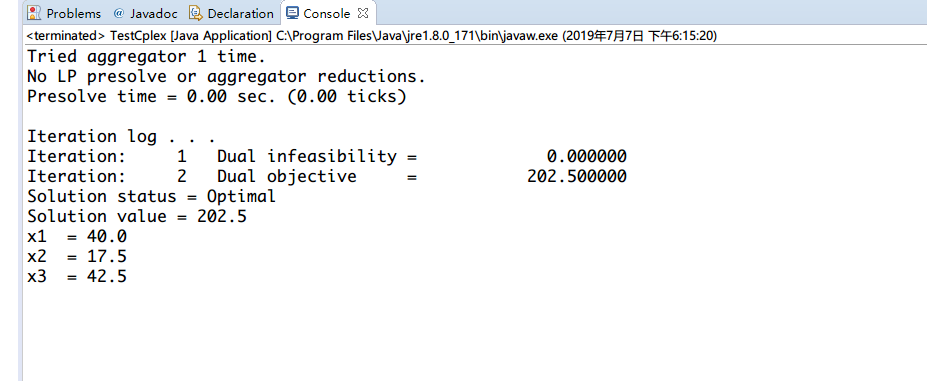
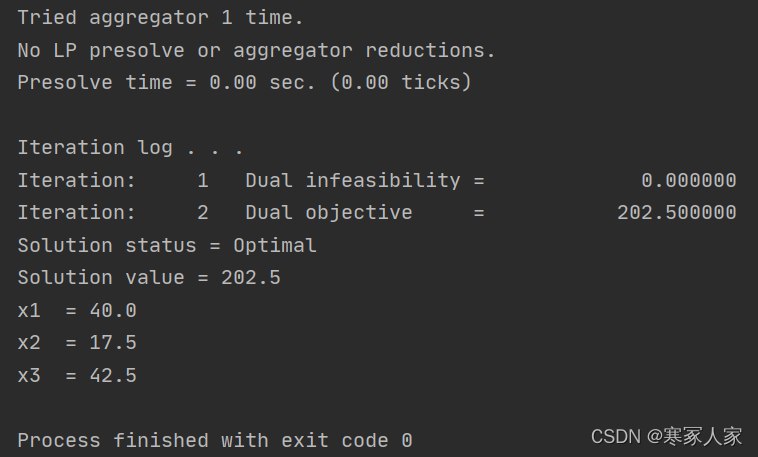
prob.solve()第七步:打印结果
#打印结果
# solution.get_status() returns an integer code
print("求解状态 = ", prob.solution.get_status(), ":")
print("目标函数值 = ", prob.solution.get_objective_value())
x = prob.solution.get_values()
print('x变量',x)

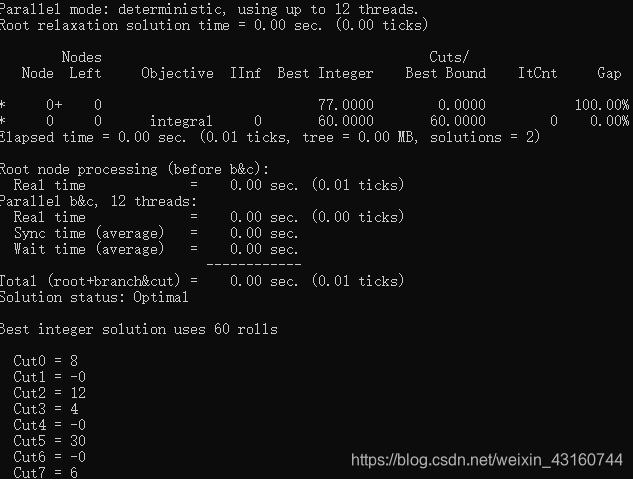
总结
cplex适合求解线性规划,整数规划、混合整数规划。好像不能求解非线性规划问题。


作者:电气-余登武