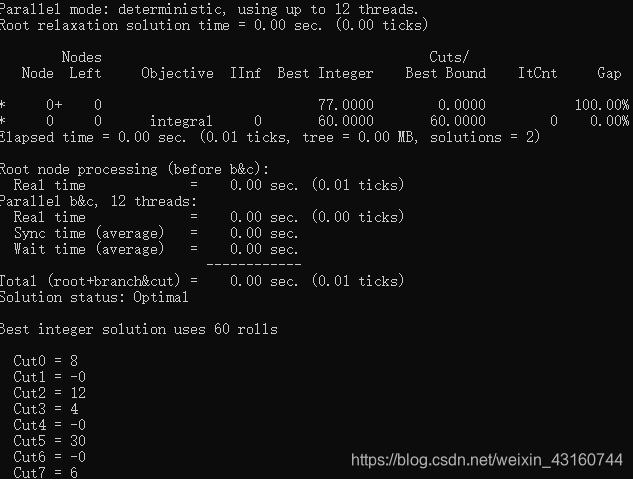
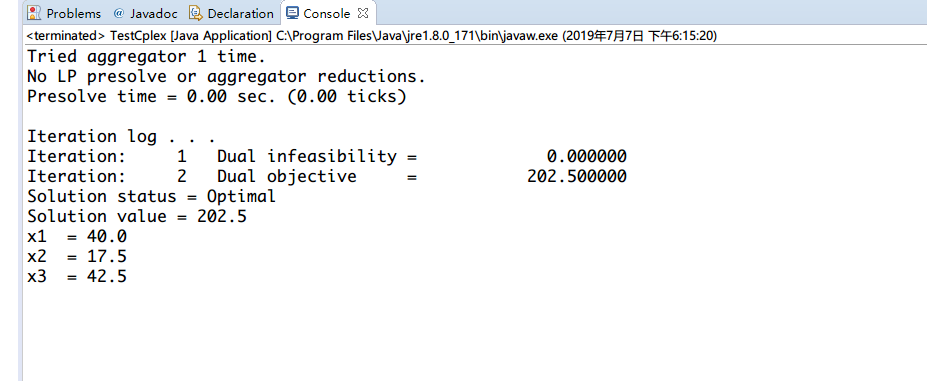
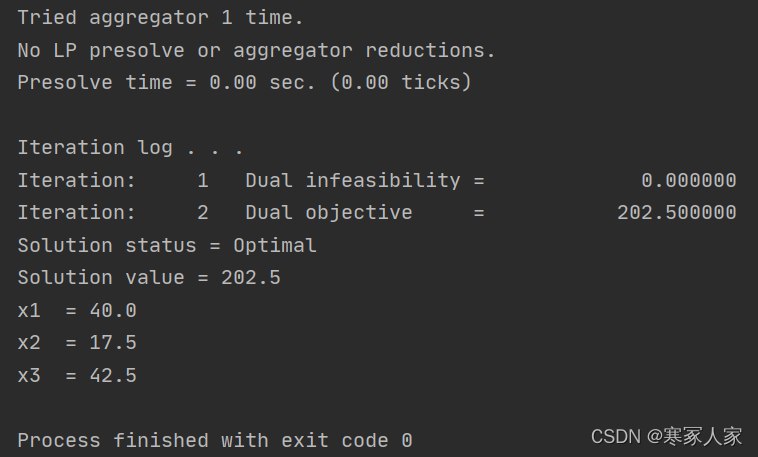
先给大家看看程序流程图：

具体求解过程如下：

1. 定义一个模型

IloCplex model = new IloCplex();

2. 定义决策变量,boolVar可以返回一个0-1的bool类型决策变量。

// define variablesIloIntVar[][] x = new IloIntVar[data.size()][data.size()];for (int i = 0; i < x.length; i++) {for (int j = 0; j < x.length; j++) {x[i][j] = model.boolVar("X[" + i + ", " + j + "]");}}

3. 添加约束1-1，addTerm将1*x[i][j]添加进表达式r里面，最终r的取值是里面所有的元素之和，也就是1*x[i][1]+1*x[i][2]+...+1*x[i][n]。

// one has only a city to go, and shouldfor (int i = 0; i < x.length; i++) {IloLinearIntExpr r = model.linearIntExpr();for (int j = 0; j < x.length; j++) {// if (i == j)// continue;r.addTerm(1, x[i][j]);}model.addEq(r, 1);}

4. 添加约束1-2，原理同上一条。

// one can only arrive to one city at a time, and shouldfor (int j = 0; j < x.length; j++) {IloLinearIntExpr r = model.linearIntExpr();for (int i = 0; i < x.length; i++) {// if (i == j)// continue;r.addTerm(1, x[i][j]);}model.addEq(r, 1);}

5. 添加约束1-3，子环约束处理有点复杂，这个也是本文重点，小编来着重给大家讲讲。注意这个约束是和下面的manager.recycle(false)判断息息相关的。

constraintFactory.cycleRestrictions(model, x, stack);约束不能产生子环stack(stack是一个栈的数据结构，里面存了构成子环的各个边)。

而后面的manager.recycle(false)，判断本次迭代cplex求解的最终解存不存在子环，如果存在，那么将子环添加进 stacks (注意这和stack不同，stacks保存的是各个子环。)，在下一轮迭代中会约束该子环的产生。

如果不存在子环，显然已经是最优解。

// add cycle restrictionsfor (Stack stack : stacks) {// stack.forEach((edge) -> System.out.println(edge.getFrom() + "->" + edge.getTo()));constraintFactory.cycleRestrictions(model, x, stack);}

子环约束处理代码如下：

public void cycleRestrictions(IloCplex model, IloIntVar[][] x, Stack combindeds) throws IloException{IloLinearIntExpr r = model.linearIntExpr();for (Edge edge : combindeds) {r.addTerm(1, x[edge.getFrom()][edge.getTo()]);}model.addLe(r, combindeds.size() - 1);}

对于每个任意节点集合combindeds，只需要combindeds里面的边数小于combindeds的节点数，就能避免产生子环。

6. 添加目标函数，z的表达式同上。

// one should complete the tour within the smallest distance possibleIloLinearNumExpr z = model.linearNumExpr();for (int i = 0; i < x.length; i++) {for (int j = 0; j < x.length; j++) {if (i == j)continue;z.addTerm(distance[i][j], x[i][j]);}}

7. 确定目标是最小化目标。

model.addMinimize(z);

8. 开始求解。

if (model.solve()) {// get tourfor (int i = 0; i < x.length; i++) {for (int j = 0; j < x.length; j++) {if (model.getValue(x[i][j]) >= 0.5) {tour.add(new Edge(i, j));}}}// repaint tour} else {System.err.println("Boi, u sick!");System.exit(1);}

注意，cplex在求解过程中会产生小数解的，虽然决策变量x[i][j]定义成了0-1变量，但是由于精度问题有可能会产生x[i][j]=0.00001或者x[i][j]=0.999999或者x[i][j]=0或者x[i][j]=1这样的数值。

model.getValue(x[i][j]) >= 0.5这个判断就是为了解决这种误差而产生的问题，当然你也可以定义成model.getValue(x[i][j]) >= 0.9、model.getValue(x[i][j]) >= 0.8、model.getValue(x[i][j]) >= 0.7等等都行。最终目的只是为了筛选那些x[i][j]=0.999999的边而已。

最终还是要进行一个判断，该判断是和上面的子环约束息息相关的：

boolean done= manager.recycle(false);if (done) {break;}

manager.recycle(false)判断的是求解的结果各边是否能构成一个Hamilton回路，因为整个程序是写在一个死循环里面不断迭代的:

while (true) {try {模型求解boolean done= manager.recycle(false);if (done) {break;}}

如果能构成一个Hamilton回路，break跳出死循环。如果不行，那么会把出现的子环更新进stacks，进行下一次迭代，重新调用cplex，在新的子环约束下，再把模型给求解一次。

然后讲讲怎么判断的，取决于参数all有两种判断方式：

1)all == true, 判断是tour是否只有一个环，如果是，那么满足Hamilton回路。

2)all == false,找看看有没有子环。如果环的size == tour的size，那么该环满足Hamilton回路。

public boolean recycle(boolean all) {Stack cycle = new Stack();HashSet visited = new HashSet();int count = 0;if (all) {// all cycleswhile (visited.size() != tour.size()) {count++;for (Edge edge : this.tour) {if (!visited.contains(edge.getFrom())) {visited.add(edge.getFrom());Stack tmp = new Stack();tmp.add(edge);while (tmp.peek().getTo() != edge.getFrom()) {Edge toPush = null;for (Edge walk : this.tour) {if (walk.getFrom() == tmp.peek().getTo()) {visited.add(walk.getFrom());toPush = walk;break;}}tmp.add(toPush);}this.stacks.add(tmp);break;}}}return (count == 1);} else {// smallest cycle//System.out.println("tour size = "+tour.size());for (Edge edge : this.tour) {if (!visited.contains(edge.getFrom())) {visited.add(edge.getFrom());Stack tmp = new Stack();tmp.add(edge);while (tmp.peek().getTo() != edge.getFrom()) {Edge toPush = null;for (Edge walk : this.tour) {if (walk.getFrom() == tmp.peek().getTo()) {toPush = walk;break;}}if (toPush == null) {for (int i = 0; i < this.stacks.size(); i++) {Stack toRelief = this.stacks.get(i);if (toRelief.contains(tmp.peek()) || toRelief.contains(edge)) {this.stacks.remove(toRelief);}}break;}visited.add(toPush.getFrom());tmp.push(toPush);}if (cycle.size() == 0 || tmp.size() < cycle.size()) {cycle.clear();cycle.addAll(tmp);}}}stacks.add(cycle);return cycle.size() == tour.size() ? true : false;}}