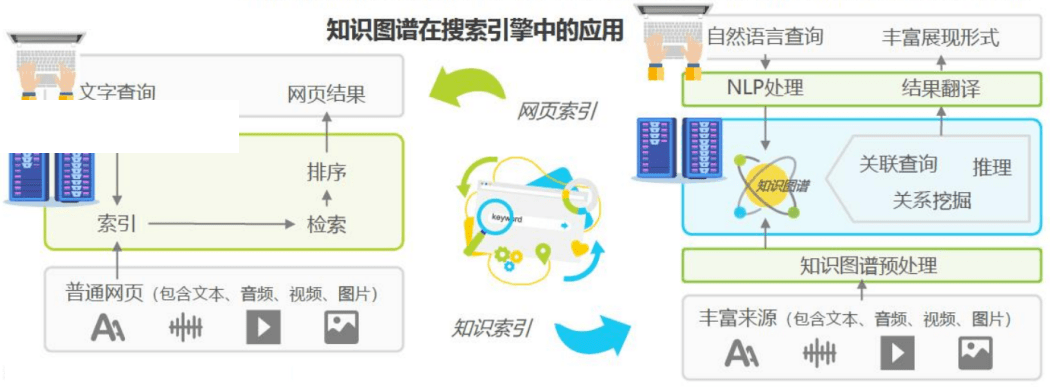
废话不多说，先上效果演示（doge）:

1、需求分析

给定一个小球，在离地某高度处给予一初始速度，当其撞击到地面后，速度衰减为原来的α倍，当其速度衰减为初始速度的1%后，运动结束。

2、运动学分析

2.1 撞击地面前

这是一个非常典型的斜抛运动，当小球没有撞击到地面前，可以将其分解为水平方向的匀速直线运动和竖直方向的匀加速直线运动。

运动学公式如下：

2.2 撞击地面后

撞击地面后，x方向上的速度和y方向上的速度各衰减为原来的α倍。

实际上，可以将完整的运动过程视为若干段斜抛运动的叠加，即下一段的斜抛运动的终点是上一段的起点，下一段运动的初始速度与与上一段运动的末速度可由下式计算：

思路确定以后，就可以开始用代码实现了！

3 代码实现

本次使用numpy和turtle来进行演示。

完整的代码放在github上了，可以点击Ball_Bouncing，下面是部分实例。

import numpy as np
import turtlev0 = 20  # 初速度（m/s）
theta = np.radians(30)  # 初始化抛射角（rad）
g = 10  # 重力加速度（m/s2）
x = 0  # 任意时刻，x方向坐标
y = 0  # 任意时刻，y方向坐标
t = 0  # 起始时间设置为0
attenuation_factor = 0.8  # 每次小球撞击地面后，速度的衰减倍率
x_init = [0]  # t = 0 时x方向的坐标
y_init = [100]  # t = 0时y方向上的坐标，即起始高度
x_array = []  # 用于存储所有时刻，x方向上坐标
y_array = []  # 用于存储所有时刻，y方向上坐标v_x_init = v0 * np.cos(theta)  # 斜抛运动x方向上的初速度
v_y_init = v0 * np.cos(theta)  # 斜抛运动y方向上的初速度while v_x_init >= 0.01 * v0 * np.cos(theta):  # 如果x方向上的速度衰减为原来的1%，则退出循环if (y > 0) or (y == 0):  # 如果小球依然在空中# 分别计算x, y方向上的速度v_x = v_x_initv_y = v_y_init - g * t

有用的话点个Star哦，谢啦！