强化学习笔记-07 n-step Bootstrapping 多步TD时分学习

article/2025/10/22 14:41:10

本文是博主对《Reinforcement Learning- An introduction》的阅读笔记，不涉及内容的翻译，主要为个人的理解和思考。

上一节介绍了TD算法，其采用了Bootstrapping方法，当前过去的预估以及即期收益来更新累积收益函数：

$G_n(s,a)=R + \gamma Q_\pi (s', a')$

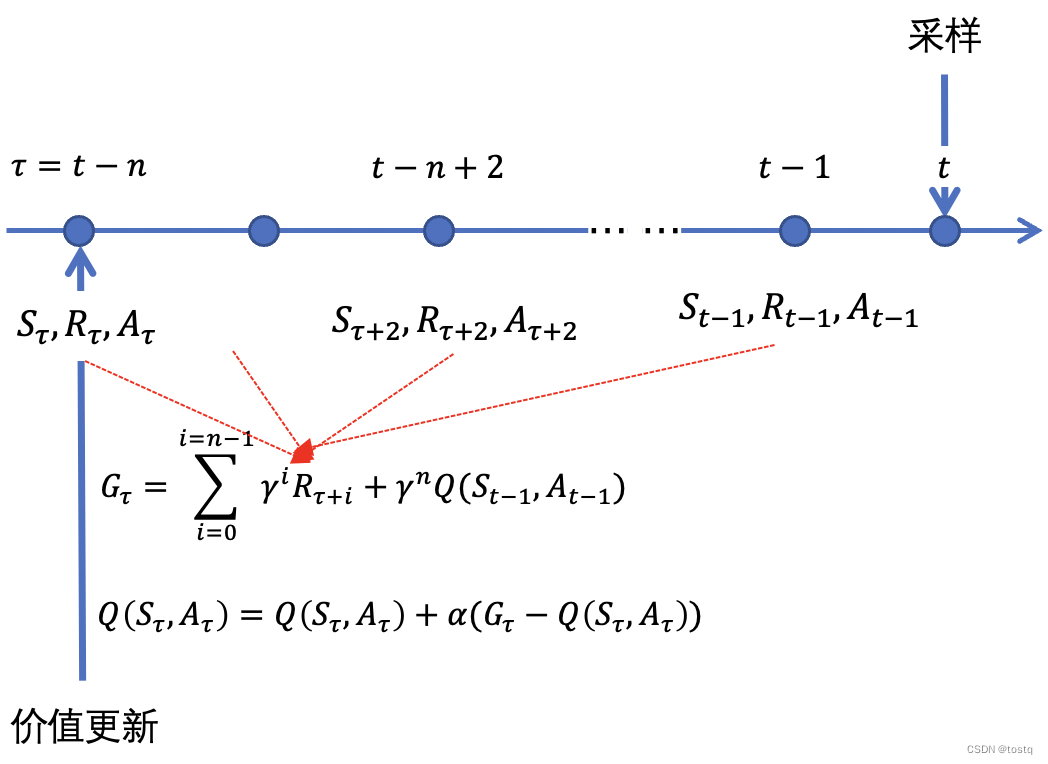
前文我们提到，通过Bootstrapping TD算法，相比于蒙特卡罗法，可以加快学习速度，但另一方面在更新累积收益函数时会存在可能偏差。而n-step TD算法就是两种算法的中间结合，其在经过n步的蒙特卡罗法采样后，再通过Bootstrapping来预估后续收益，其累积收益函数的更新可以表示为：

$G_{t:t+n}(s,a)=\sum_{i=0}^{n-1} \gamma^{i} R_{t+i} + \gamma^n Q_\pi (s', a')$

在一些情况中，在单步中很难获得有意义的即时reward，另一方面又想要加快学习速度，n-step TD算法就非常适合，其可以在真实采样n步后，当到达一个有意义的状态后，再通过Bootstrapping来加快训练。n-step TD算法实际上是TD算法结合MC的一个变种。其价值函数的更新也可以改写为：

$Q_{n}(s,a)=Q_{n-1}(s,a) + \alpha (G_n(s,a)-Q_{n-1}(s,a))$

下图描述了n-step TD算法整体采样以及更新步骤，图中描述了在t时刻完成动作采样，转换下一状态后，更新t-n时刻的价值函数的过程。

1. on-policy or offline-policy

on-policy和off-policy算法的不同主要不同在于采样动作时，是依赖于target-policy还是behavior-policy。简单来说，对于on-policy算法，采样是通过目标policy函数来选择的，而目标policy函数是在完成价值函数更新后进行修正的。

而off-policy定义了另一个behavior-policy来完成采样，其同价值函数更新后所修正的目标policy函数不同，其主要是为了explore。因此behavior-policy和target-policy之前的不同，会导致累积收益函数之前存在偏差，其需要通过重要性采样方式来修正。

$\rho(A_t ,S_t )=\frac{\Pi^{n-1}_{i=0} \pi_\tau (A_{t+i}|S_{t+i})}{\Pi^{n-1}_{i=0} \pi_b(A_{t+i}|S_{t+i})}\\ Q(S_{t}, A_{t})=Q(S_{t}, A_{t}) +\alpha \rho(A_t ,S_t)(G_t^b-Q(S_{t}, A_{t}))$

2. n-step Tree Backup Algorithm

上节提到在off-policy策略，其引入了behavior-policy来完成样本采样，然后通过重要性采样来调整target-policy之间的偏差，本节所介绍Tree Backup方法，不是通过重要性采样来扭偏，而是直接通过target-policy来调整，下图介绍整体逻辑，其类似于上一篇所说的Expected on-policy方法。

上述的公式在求解 $G(S_t,A_t)$ 时，需要用到 $G(S_{t+1},A_{t+1})$ ，以及其他子路径的估计值 $Q(S_t,a)$ ，这种树形回溯计算的方式因此称之为Tree Backup算法。

3. 统一的算法

on-policy算法直接通过target-policy进行采样，而off-policy算法或者通过采用behavior-policy+重新性采样，或者类似于Tree Backup引入了期望估计的方法。on-policy方法收敛速度更快，但off-policy更可能找到最优点，因此一种统一算法是设定某个概率值 $\sigma$ 来随机选择每步是用on-policy直接采样计算，还是通过off-policy算法进行更新，这种方式能综合两种策略的优点，称之为n-step Q( $\sigma$ )算法。