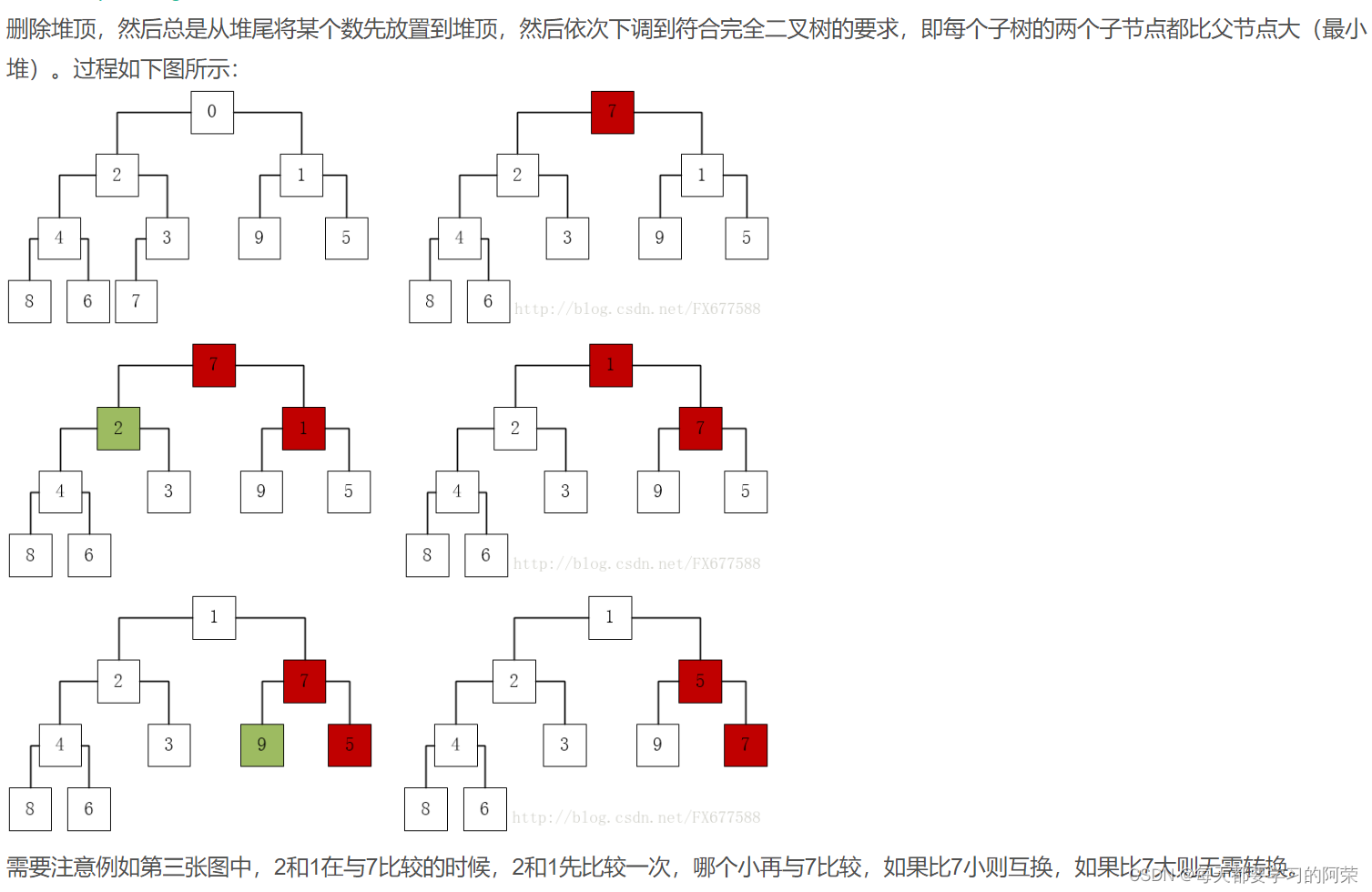
同态加密的Bootstrapping操作最早由Gentry在他的博士论文里提出，是实现分级同态加密到全同态加密之间转换的关键步骤。目前所有的bootstrapping工作都是基于Gentry的这个想法，未有出其右者。

这篇博客打算讲一下Bootstrapping的原理，同时看一下在CKKS中，Bootstrapping是怎么实现的。

为了理解Bootstrapping的原理，我们首先看一个故事。

故事

Alice是一个资深的珠宝加工匠，她也管着一家珠宝店，某个聪明的年轻人Bob是她的学徒。

俗话说教会徒弟饿死师傅。Alice不想让Bob看到珠宝加工的每一个步骤执行之后半成品是什么样子的，因为如果Bob看见了加工过程中每一步的中间件的话，他就能悟出来加工的全过程，然后自己出来单干，用效率和年龄卷死自己。

不信的话，可以让另一个人在你的背上划拉一个字，对比一下看到划拉字的全过程和只靠触觉的话，辨识出来这个字是啥的可能性有多大。

但是两个人干活总是比一个人干活的产出要多。Alice舍不得撵走这样一个好用的劳动力。

Alice的核心需求：让Bob在看不见珠宝胚子的情况下还能做加工。

这天Alice发明了一个手套箱子，就像下面这张图里的一样：

只见这手套箱：

通体漆黑，从外面看不到里面有什么东西。有两扇门，一扇门上了锁，在开锁了之后可以往外取东西也可以往里放东西；另一扇门是单向的，可以往里面扔任何的东西，但是拿不出来。

于是Alice把手套箱交给Bob，让他来做珠宝加工。具体地，每次Alice会把珠宝坯子扔到手套箱里，让Bob对它按照固化的流程进行加工。等到加工完了之后，Alice再把手套箱的锁打开，把成品取出来。

如此这般这般如此了一段时间之后，Alice发现Bob隔着手套箱摸索着工作效率不行，以及由于手套箱自身设计的原因，在每一步加工过程中都会引入一些误差，相应地，在一个手套箱里加工珠宝最多只能加工L次，否则误差积累到足够大之后，在手套箱里的珠宝就会被加工废掉，成了残次品了。Alice暂时的解决方案是隔几个步骤就把中间件拿出来，自己再精琢一番，但是这么做实在是太费事了。

直到有一天，Alice又买了一个手套箱。为了区别，旧有的手套箱叫手套箱A，新买的手套箱叫手套箱B。

Alice自己把两个手套箱的钥匙都做了备份。今天开工前，Alice把坯子放在了手套箱A里，然后把手套箱A的钥匙放在了手套箱B中。

于是，当Bob隔着手套箱A做了若干次加工之后，他就把手套箱A整个扔到了手套箱B中。用已经放在手套箱B中的A的钥匙把A中的半成品取出来，在手套箱B中继续加工。

现实

到这里故事就讲完了。和现实世界对比，很显然珠宝坯子是私密数据，手套箱是同态加密方案，单向门意味着公钥，钥匙就是私钥。

这里的手套箱套娃操作，其实就是bootstrapping了。

本质上，bootstrapping这个操作就是在密文下走完解加密的一个流程。

一般的同态加密涉及加密、运算和解密三样东西。可以看到，手套箱故事能不能拿到现实中来应用，很大程度上取决于能不能在加密的情况下实现加解密函数。

而这不是一个简单的事情。

CKKS方案的Bootstrapping操作

CKKS方案的实现其实和Gentry的想法不完全一样。
在CKKS方案里没有用到对$s$的加密结果，而是在密文下做了一遍解码和编码。

首先看一下CKKS方案的主要API和主要原理。可以参考这里，也可以看下面的图。当然了，这两篇文章里可能有一些地方表述不清甚至会出错，但是本文的目的不在于严谨地介绍，只是给大家留下一个大概印象方便更好地理解原文。
为了方便，首先放一个CKKS方案的主要API：

这里着重提一下CKKS的编码和解码问题。

在我的CKKS介绍文章里，我提到过里面的向量编码需要做一个插值。具体地，考虑分圆多项式的原根 ${\xi }_i$ 和明文向量的分量 $m_i$ ，插值（编码）后生成一个多项式 $p$ ，通过 $p({\xi }_i)=m_i$ 来确定 $p$ 的系数。

我们也提到过编码和解码可以用SIMD（单条指令操纵多条数据）的方式并行计算。比如，解码操作可以写成：
$$m=Up$$
其中这里的 $p$ 是多项式 $p$ 的系数组成的向量，$U$见下图。通过并行计算手段（GPU/FPGA等）对矩阵运算进行加速。

想要实现编码的话，只需要把这个过程倒过来就行了。

CKKS Bootstrapping方案中的一些预备知识

这一部分的东西，如果觉得看不明白，可以先跳到下一部分，直接把握Bootstrapping的脉络，根据脉络中的问题，再回来看各个细节。

首先，分析一下CKKS解密的方法：
$$m=(c_0+c_{1}s)\mathrm{mod}q$$

这里的主要步骤有两个：一个是计算 $c_0+c_{1}s$，一个是计算 $F(x)=x\mathrm{mod}q$。

但是这个$F$是不连续的周期函数。我们想给它搞一个近似玩一玩。

我们给出一个前提条件：明文多项式 $m$ 中系数的规模和 $q$ 相比很小。其实这个事情可以办到，因为你完全可以在还剩足够多的乘法深度的时候就解密。

于是，我们对照着上面的前提条件，重新写一下解密的过程：
对某个level $l$下的一个密文$(c_0,c_1)$进行解密：
$$t=(c_0+c_{1}s)\mathrm{mod}{Q}_l$$

这里，$t=qI+m$，其中 $|I|<K$，$K$是一个正整数。

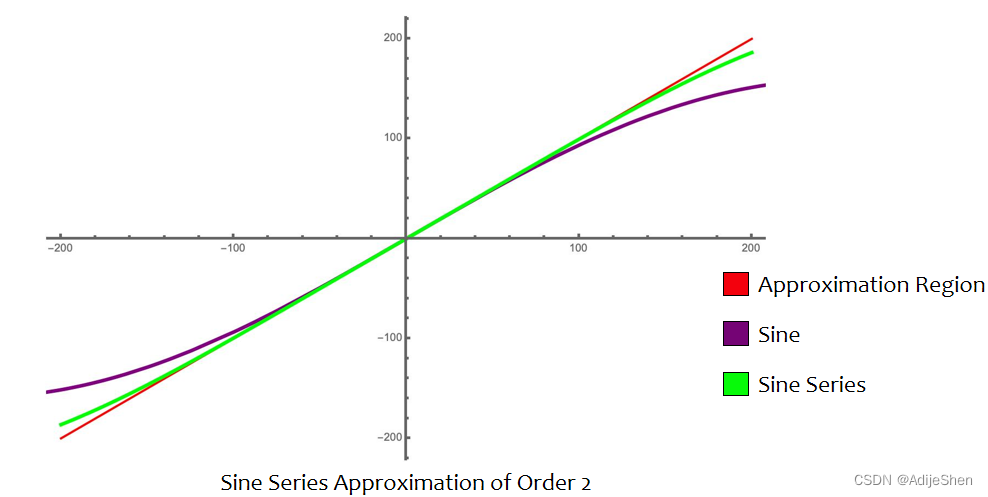
这个时候，我们可以用正弦函数（泛指数函数）对 $F[t]=t\mathrm{mod}q$ 进行近似。

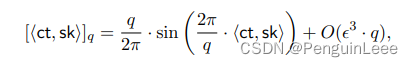
但是因为同态加密只支持加法和乘法，所以可以使用泰勒展开或者切比雪夫展开。

在CKKS方案中，还涉及到在密文情况下进行矩阵-向量乘法的操作。这里我们用一张图来表示一个经典的矩阵-向量乘法的步骤，使用到了CKKS全部的API——向量加法、向量乘法和重线性化、以及旋转操作。

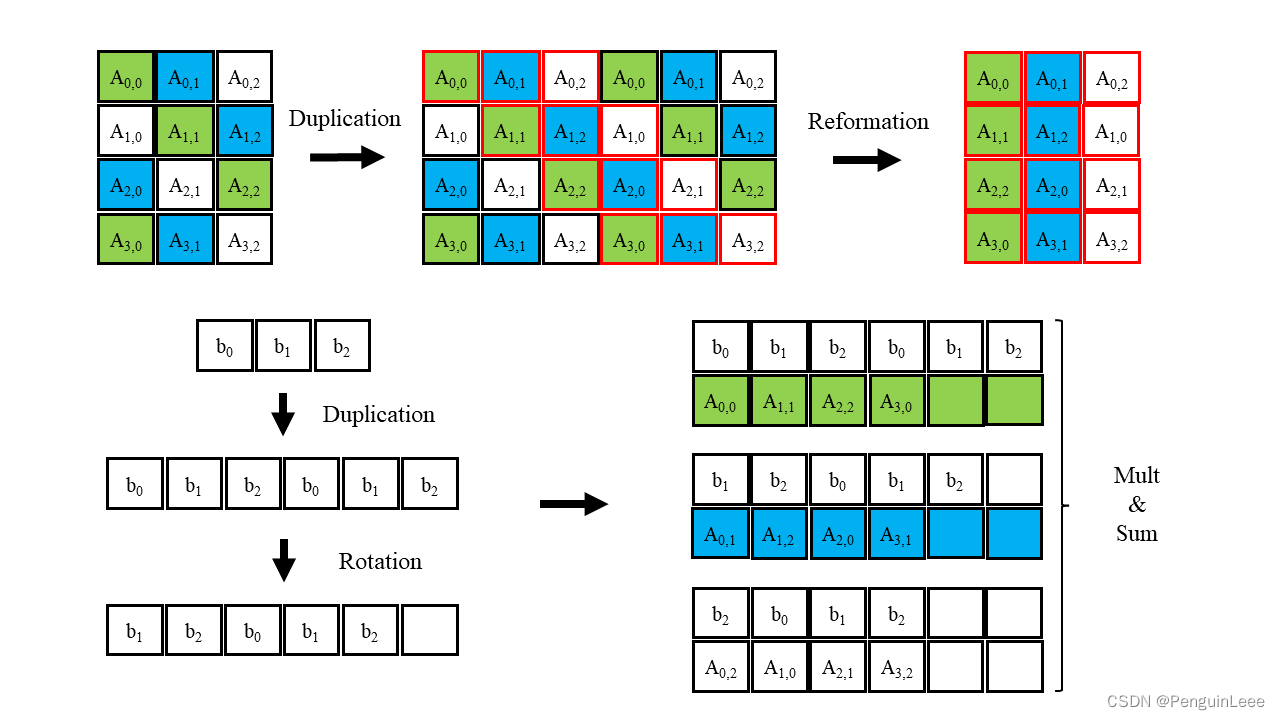
CKKS Bootstrapping方案大体逻辑介绍

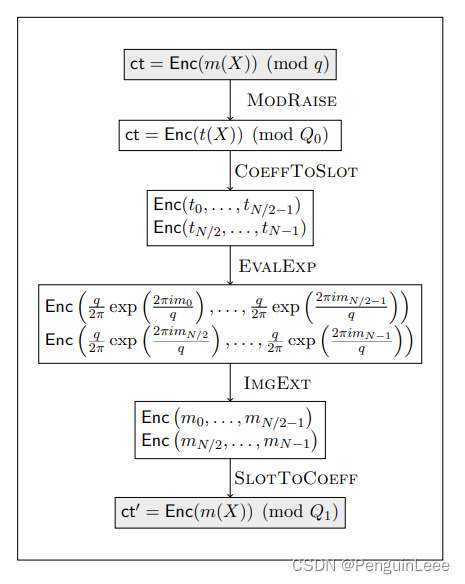
如图。

分为模数提升、解码、正弦近似、编码四个部分。都在密文下完成。

第一步，我们已有一个层数耗尽的密文$ct=(c_0,c_1)\mathrm{mod}{Q}_l$，对应的明文多项式是$m(X)=(c_0+c_{1}s)\mathrm{mod}q$。

但是如果解密的过程中不模$q$（或者模一个远大于$q$的数$Q_0$）的话，记$t(X)=(c_0+c_{1}s)\mathrm{mod}{Q}_0$，这里就有$t=qI+m$。其中$I$是一个不太大的整数。那么有：
$$(c_0+c_{1}s)\mathrm{mod}{Q}_0=t(X)$$
体现在密文之中，就是 $c_0,c_1\mathrm{mod}{Q}_l$ 的模数被提升，重新改写成 $c_0,c_1\mathrm{mod}{Q}_0$了。
注意，这里的$Q_0$和$Q_l$都是$q$的倍数。

在这一步的执行中我们发现，对模数提升前后的$(c_0,c_1)$进行解密：$m(X)=(c_0+c_{1}s)\mathrm{mod}q$，最后都是需要模$q$的。这意味着，模数提升前后的$(c_0,c_1)$，解密后对应着相同的$m$。

做了这一步模数提升之后，我们又可以做很多的乘法运算了。

第二步，我们把加了密的明文多项式$t(X)=(c_0+c_{1}s)\mathrm{mod}{Q}_0$做密文下的解码运算。这里的解码的意思是，把$t(X)$中的$X$用原根进行带入，得到解码后的向量$t\mathrm{mod}{Q}_0$，可以通过前文所说的矩阵-向量乘法进行实现。

但是由于“编码”和“解码”的可逆性，$t$包含的信息并没有被消除。

第三步，我们要对$t\mathrm{mod}{Q}_0$在密文下进行正弦近似，得到$t\mathrm{mod}q=m$，即获得真正的明文$m$（因为由于模数的存在，$m$和$t\mathrm{mod}{Q}_0$本质上还是不同的）。

最后，在密文下重新走一遍编码的流程，把$t$变成$t(X)$。于是Bootstrapping的操作就完成了。

现在已有的一些改进Bootstrapping的工作，很多都是在此基础上进行的优化。