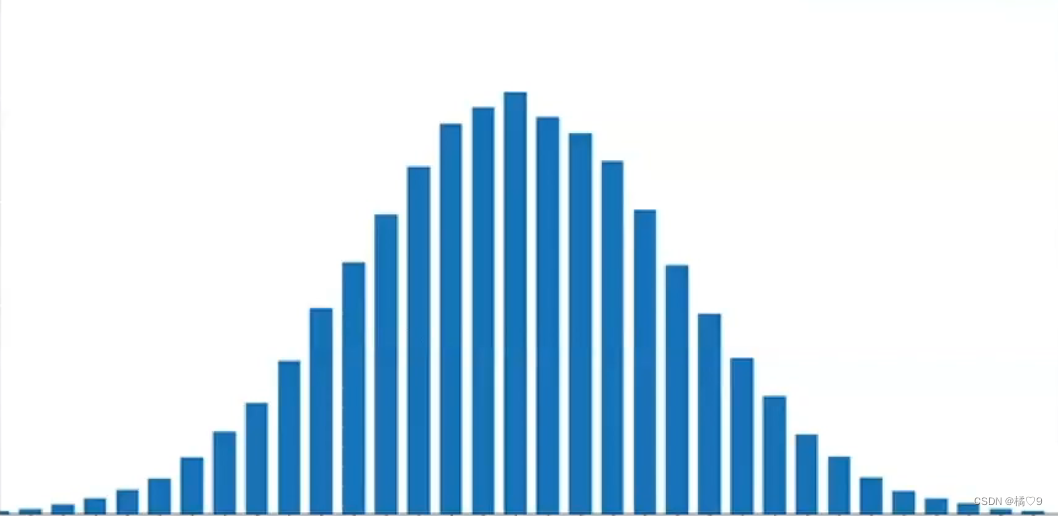
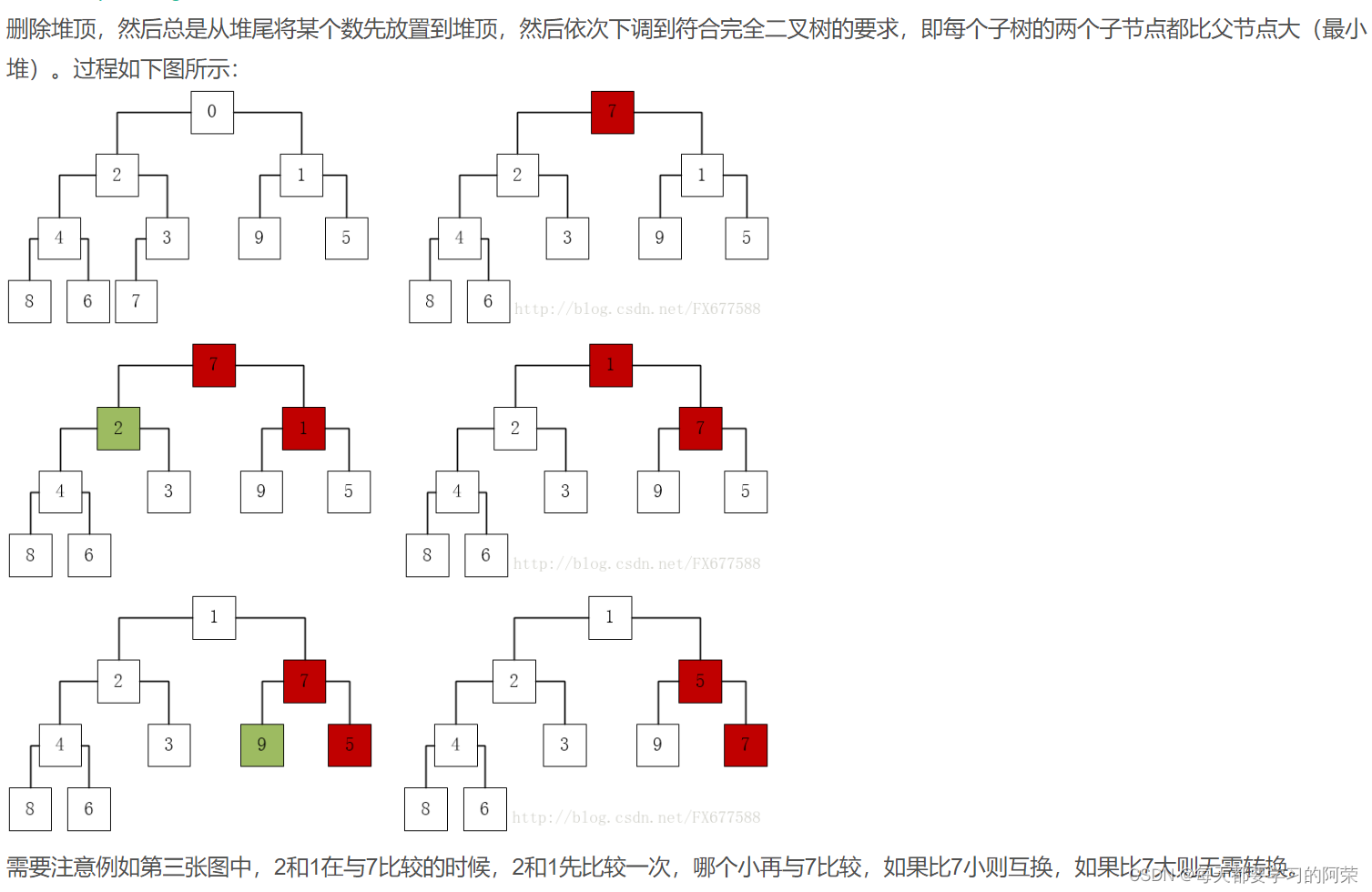
Bootsrapping指的就是利用有限的样本资料经由多次重复抽样，重新建立起足以代表母体样本分布的新样本。

统计中我们常常需要做参数估计，具体问题可以描述为：给定一系列数据

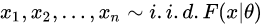
假设它们是从分布F中采样得到的，参数估计就是希望估计分布F中的θ。θ可以是均值，标准差(Standard Deviation)，标准误差(Standard Error)。

bootstrapping算法的目的就是为了估计从而得到的分布的预测。具体地，它的思想对已有的观测值进行多次重复的抽样，每次抽样都可以得到一个预测的经验分布函数，根据这些不同抽样得到的经验分布函数，可以得到一个更好的关于统计量分布的估计。

打个比方，如果现在有N个学生的身高数据，需要估计的统计量是学生的平均身高。bootstraping的方法可以替我们确定身高平均值的置信区间。步骤大致如下：

1.从N个数据中随机抽取M个数据（有放回）构成一个样本
2.计算每个样本的均值
3.重复步骤1，2知道计算足够多的次数（至少多于20-30次）

根据这些步骤得到的100次结果，我们可以得出95%的置信区间，即覆盖了95%的样本均值的区间。换言之，超出这个范围的身高均值，出现的次数都小于5%，也可以说它的p值<0.05。以上所说的可以理解为bootstrapping百分位法，它假设样本均值与总体均值的分布大致相似，但这个假设在现实中很难保证成立。

---

总结

1. 确定数据集数据量N
2. 确定每次抽取数据M的大小(M≤N)
3. 重复操作若干次，次数越大越好
   1. 有放回地抽取数据量为N的训练集a
   2. 用训练集a训练模型model
   3. 剩下的没用的数据组成预测集b，用b来预测
4. 计算模型model的均值（就是你要求的θ）

python举例：


可以直接用scikit-learn包里的resample()

# scikit-learn bootstrap
from sklearn.utils import resample
# data sample
data = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6]
# prepare bootstrap sample
boot = resample(data, replace=True, n_samples=4, random_state=1)
print('Bootstrap Sample: %s' % boot)
# out of bag observations
oob = [x for x in data if x not in boot]
print('OOB Sample: %s' % oob)

在这里Bootstrap Sample= [0.6, 0.4, 0.5, 0.1]，OOB Sample=0.2, 0.3]

传统的区间估计往往需要先知道的分布，但这有点陷入鸡生蛋蛋生鸡的困境了。相反的，bootstrapping方法则无需已知分布，提供了一种灵活的判断统计量的方法。在做机器学习或者深度学习实验室，往往有些实验结果会被要求提供p值。一个可行的方法就是使用bootstrapping。将测试集中的数据做随机抽样得到一些样本，通过模型预测得到每个样本关于某metric的平均值，这样就能计算出其p值了。

参考资料：
理解bootstrapping
A Gentle Introduction to the Bootstrap Method