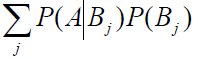朴素贝叶斯基本原理和预测过程、先验概率、后验概率、似然概率概念

article/2025/9/8 1:49:31

贝叶斯原理是英国数学家托马斯·贝叶斯提出的。

贝叶斯原理

建立在主观判断的基础上：在我们不了解所有客观事实的情况下，同样可以先估计一个值，然后根据实际结果不断进行修正。

举例：

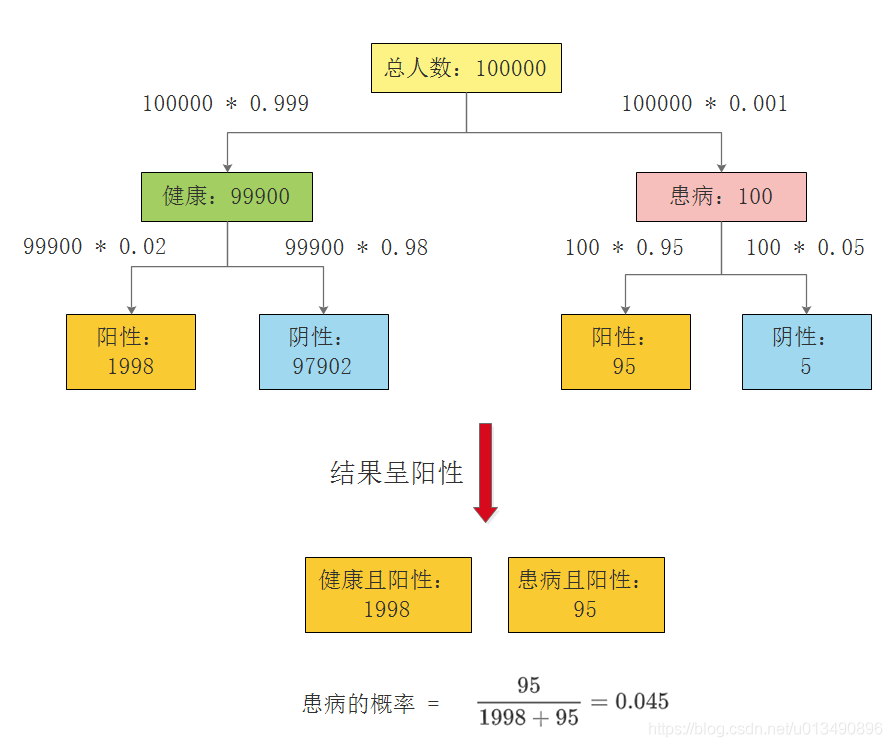
一个袋子里有10个球，其中6个黑球，4个白球；那么随机抓一个黑球的概率是0.6！（已知黑球白球数量—了解事情再判断）

如果我们事先不知道袋子里面黑球和白球的比例，而是通过我们摸出来的球的颜色，能判断出袋子里面黑白球的比例么？（未知事情全貌—还能判断吗？）

三个概率：

先验概率：通过经验来判断事情发生的概率。一般都是单独事件概率，如 $P (x) 、 P (y)$
后验概率：发生结果A之后，推测原因B的概率 $P (B ∣ A)$
条件概率：事件 A 在另外一个事件 B 已经发生条件下的发生概率，表示为 $P (A ∣ B)$ 。

P(y|x) 是后验概率，一般是我们求解的目标。P(x|y) 是条件概率，又叫似然概率，一般是通过历史数据统计得到。一般不把它叫做先验概率，但从定义上也符合先验定义。P(y) 是先验概率，一般都是人主观给出的。贝叶斯中的先验概率一般特指它。P(x) 其实也是先验概率，只是在贝叶斯的很多应用中不重要（因为只要最大后验不求绝对值），需要时往往用全概率公式计算得到。

贝叶斯原理就是求解后验概率
贝叶斯公式：
$\frac{P(x|y) * P(y) }{P(x)}$

似然函数（likelihood function）：

把概率模型的训练过程理解为求参数估计的过程。似然在这里就是可能性的意思，它是关于统计参数的函数

最大似然理论：

认为P(x|y)最大的类别y，就是当前文档所属类别。
即 $Max P(x|y) = Max\{ p(x1|y)*p(x2|y)*...p(xn|y)\}$ for all y

贝叶斯理论：
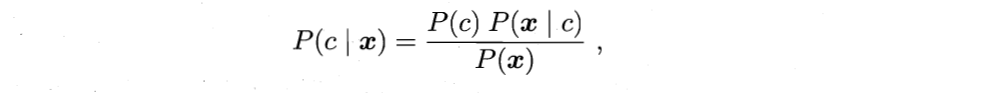
在这里插入图片描述

认为需要增加先验概率p(y)，因为有可能某个y是很稀有的类别几千年才看见一次，即使P(x|y)很高，也很可能不是它。
所以 $y = M a x P (x ∣ y) * P (y)$ , 其中p(y)一般是数据集里统计出来的。

朴素贝叶斯

假设每个输入变量是独立的

朴素贝叶斯模型由两种类型的概率组成：

每个类别的概率P(Cj)；
每个属性的条件概率P(Ai|Cj)。

训练朴素贝叶斯模型，我们需要先给出训练数据，以及这些数据对应的分类。
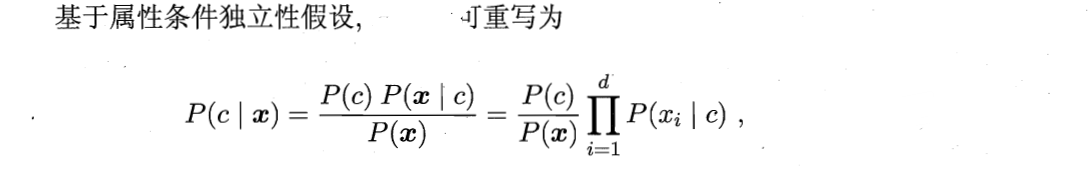
在这里插入图片描述
对于所有类别来说P(x)相同，则：

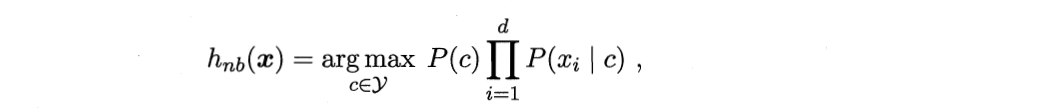
贝叶斯原理、贝叶斯分类和朴素贝叶斯区别

贝叶斯原理是最大的概念，它解决了概率论中“逆向概率”的问题
在这个理论基础上，人们设计出了贝叶斯分类器，
朴素贝叶斯分类是贝叶斯分类器中的一种，也是最简单，最常用的分类器。(朴素贝叶斯之所以朴素是因为它假设属性是相互独立的)

朴素贝叶斯预测过程

朴素贝叶斯分类常用于文本分类，尤其是对于英文等语言来说，分类效果很好。它常用于垃圾文本过滤、情感预测、推荐系统等。

第一阶段：准备阶段

需要确定特征属性
并对每个特征属性进行适当划分，然后由人工对一部分数据进行分类，形成训练样本。

(分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。)

第二阶段：训练阶段

生成分类器
主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率。

第三阶段：应用阶段

使用分类器对新数据进行分类。
输入是分类器和新数据，输出是新数据的分类结果。

贝叶斯算法的优缺点

优点：

朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。
对缺失数据不太敏感，算法也比较简单，常用于文本分类。

缺点：

理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
对输入数据的表达形式很敏感。