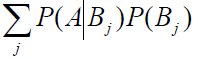先验概率、似然函数与后验概率

先验概率

Prior probability

 

在贝叶斯统计中，先验概率分布，即关于某个变量 p 的概率分布，是在获得某些信息或者依据前，对 p 的不确定性进行猜测。例如， p 可以是抢火车票开始时，抢到某一车次的概率。这是对不确定性（而不是随机性）赋予一个量化的数值的表征，这个量化数值可以是一个参数，或者是一个潜在的变量。

 

先验概率仅仅依赖于主观上的经验估计，也就是事先根据已有的知识的推断，

 

在应用贝叶斯理论时，通常将先验概率乘以似然函数（likelihoodfunction）再归一化后，得到后验概率分布，后验概率分布即在已知给定的数据后，对不确定性的条件分布。

 

似然函数

 

似然函数（likelihood function），也称作似然，是一个关于统计模型参数的函数。也就是这个函数中自变量是统计模型的参数。对于结果 x ，在参数集合 θ 上的似然，就是在给定这些参数值的基础上，观察到的结果的概率 L(θ|x)=P(x|θ) 。也就是说，似然是关于参数的函数，在参数给定的条件下，对于观察到的 x 的值的条件分布。

 

似然函数在统计推测中发挥重要的作用，因为它是关于统计参数的函数，所以可以用来评估一组统计的参数，也就是说在一组统计方案的参数中，可以用似然函数做筛选。在非正式的语境下，“似然”会和“概率”混着用；但是严格区分的话，在统计上，二者是有不同。

 

不同就在于，观察值 x 与参数 θ 的不同的角色。概率是用于描述一个函数，这个函数是在给定参数值的情况下的关于观察值的函数。例如，已知一个硬币是均匀的（在抛落中，正反面的概率相等），那连续10次正面朝上的概率是多少？这是个概率。

 

而似然是用于在给定一个观察值时，关于用于描述参数的情况。例如，如果一个硬币在10次抛落中正面均朝上，那硬币是均匀的（在抛落中，正反面的概率相等）概率是多少？这里用了概率这个词，但是实质上是“可能性”，也就是似然了。

 

后验概率

Posterior probability

 

后验概率是关于随机事件或者不确定性断言的条件概率，是在相关证据或者背景给定并纳入考虑之后的条件概率。后验概率分布就是未知量作为随机变量的概率分布，并且是在基于实验或者调查所获得的信息上的条件分布。“后验”在这里意思是，考虑相关事件已经被检视并且能够得到一些信息。

 

后验概率是关于参数 θ 在给定的证据信息 X 下的概率： p(θ|x) 。

 

若对比后验概率和似然函数，似然函数是在给定参数下的证据信息 X 的概率分布： p(x|θ) 。

 

二者有如下关系：

 

我们用 p(θ) 表示概率分布函数，用 p(x|θ) 表示观测值 x 的似然函数。后验概率定义如下：

 

 

 

p(θ|x)=p(x|θ)p(θ)p(x)

 

 

鉴于分母不变，可以表达成如下正比关系：

 

 

 

Posteriorprobability∝Likelihood×Prior probability

 

 

来先举一个例子：

如果有一所学校，有60%是男生和40%是女生。女生穿裤子与裙子的数量相同；所有男生穿裤子。一个观察者，随机从远处看到一名学生，观察者只能看到该学生穿裤子。那么该学生是女生的概率是多少？这里题目中观察者比如近似眼看直接不清性别，或者从装扮上看不出。答案可以用贝叶斯定理来算。

用事件 G 表示观察到的学生是女生，用事件 T 表示观察到的学生穿裤子。于是，现在要计算 P(G|T) ，我们需要知道：

P(G) ，表示一个学生是女生的概率，这是在没有任何其他信息下的概率。这也就是我们说的先验概率。由于观察者随机看到一名学生，意味着所有的学生都可能被看到，女生在全体学生中的占比是 40 ，所以概率是 0.4 。

P(B) ，是学生不是女生的概率，也就是学生是男生的概率，也就是在没有其他任何信息的情况下，学生是男生的先验概率。 B 事件是 G 事件的互补的事件，这个比例是 60 ，也即 0.6 。

P(T|G) 是在女生中穿裤子的概率，根据题目描述，是相同的 0.5 。这也是 T 事件的概率，given G 事件。

P(T|B) 是在男生中穿裤子的概率，这个值是1。

P(T) 是学生穿裤子的概率，即任意选一个学生，在没有其他信息的情况下，TA穿裤子的概率。如果要计算的话，那可以计算出所有穿裤子的学生的数量，除以总数，总数可以假设为常数 C ，但是最后会被约去。或者根据全概率公式 P(T)=P(T|G)P(G)+P(T|B)P(B) 计算得到 P(T)=0.5×0.4+1×0.6=0.8 。

基于以上所有信息，如果观察到一个穿裤子的学生，并且是女生的概率是

 

 

P(G|T)=P(T|G)P(G)P(T)=0.5×0.40.8=0.25.

 

 

这就是贝叶斯公式的一个示例，如果是两个相关的属性，我们只知道其中一些的概率分布情况，就可以根据贝叶斯公式来计算其他的一些后验概率的情况。

 

 极大似然估计和贝叶斯估计

 

极大似然估计和贝叶斯估计分别代表了频率派和贝叶斯派的观点。频率派认为，参数是客观存在的，只是未知而矣。因此，频率派最关心极大似然函数，只要参数求出来了，给定自变量X，Y也就固定了，极大似然估计如下所示:

D表示训练数据集，是模型参数

相反的，贝叶斯派认为参数也是随机的，和一般随机变量没有本质区别，正是因为参数不能固定，当给定一个输入x后，我们不能用一个确定的y表示输出结果，必须用一个概率的方式表达出来，所以贝叶斯学派的预测值是一个期望值，如下所示：

其中x表示输入，y表示输出，D表示训练数据集，是模型参数

 

  该公式称为全贝叶斯预测。现在的问题是如何求（后验概率），根据贝叶斯公式我们有：

  可惜的是，上面的后验概率通常是很难计算的，因为要对所有的参数进行积分，不能找到一个典型的闭合解（解析解）。在这种情况下，我们采用了一种近似的方法求后验概率，这就是最大后验概率。

  最大后验概率和极大似然估计很像，只是多了一项先验分布，它体现了贝叶斯认为参数也是随机变量的观点，在实际运算中通常通过超参数给出先验分布。

  从以上可以看出，一方面，极大似然估计和最大后验概率都是参数的点估计。在频率学派中，参数固定了，预测值也就固定了。最大后验概率是贝叶斯学派的一种近似手段，因为完全贝叶斯估计不一定可行。另一方面，最大后验概率可以看作是对先验和MLE的一种折衷，如果数据量足够大，最大后验概率和最大似然估计趋向于一致，如果数据为0,最大后验仅由先验决定。

转自：https://www.cnblogs.com/wjgaas/p/4523779.html

参考资料：

 [1] Machine learning: a probabilistic perspective 第三章

 [2]Andrew Ng讲义，Regularization and model selection

    http://v.163.com/special/opencourse/machinelearning.html