概率定义

先验概率：事件发生前的预判概率。可以是基于历史数据的统计，可以由背景常识得出，也可以是人的主观观点给出。一般都是单独事件概率，如P(x),P(y)。
后验概率：事件发生后求的反向条件概率；或者说，基于先验概率求得的反向条件概率。概率形式与条件概率相同。
条件概率：条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为：P（A|B），读作“在B的条件下A的概率”。
数学期望：试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。
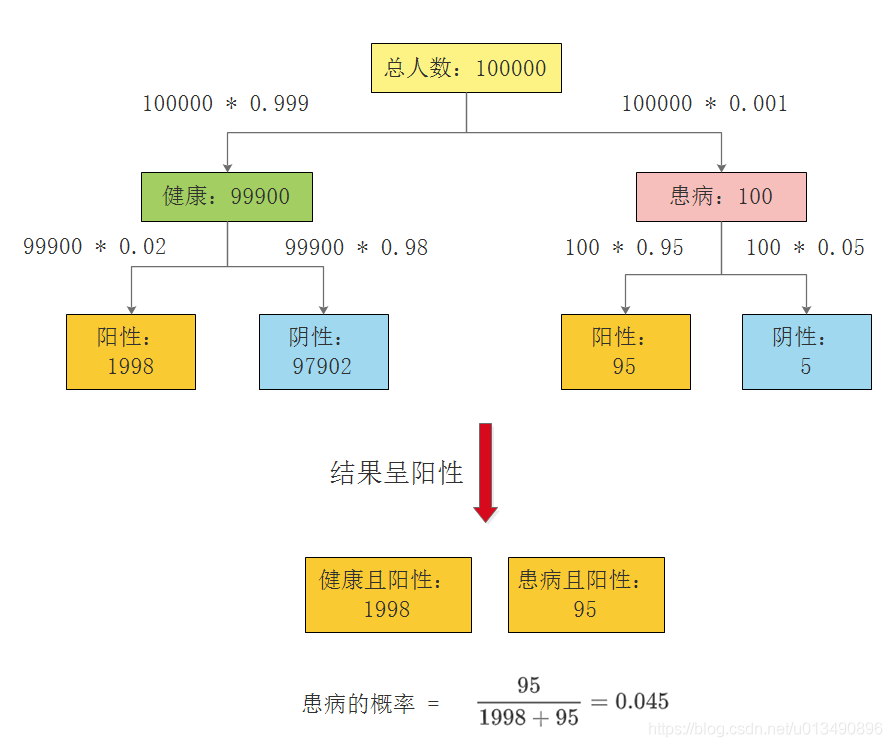
似然函数：似然则用来描述已知随机变量输出结果时，未知参数的可能取值。
（常说的概率是指给定参数后，预测即将发生的事件的可能性，而似然概率正好与这个过程相反，我们关注的量不再是事件的发生概率，而是已知发生了某些事件，我们希望知道参数应该是多少。）
联合分布函数：概率P既受x影响又受到y影响。p(x,y)
最大后验概率：在贝叶斯统计学中，“最大后验概率估计”是后验概率分布的众数。
贝叶斯估计：是利用贝叶斯定理结合新的证据及以前的先验概率，来得到新的概率。它提供了一种计算假设概率的方法，基于假设的先验概率、给定假设下观察到不同数据的概率以及观察到的数据本身。
极大似然估计：极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！
L1,L2范数：L1范数是指向量中各个元素的绝对值之和，L2范数是指向量各元素的平方和然后开方
加权平均值：各数值乘以相应的权数，然后加总和得到总体值，再除以单位数
标准差：离均差平方的算术平均数的算术平方根，用σ表示
超平面：超平面是指n维线性空间中维度为n-1的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中，一条直线是一维的，它把平面分成了两块；三维空间中，一个平面是二维的，它把空间分成了两块。
势函数：满足下面条件的连续函数f(x)称为势函数。
边缘分布函数：如果二维随机变量X,Y的分布函数F{x,y}为已知，那么随机变量x，y的分布函数FX{x}和Fʏ{y}可由F{x,y}求得。则FX{x}和Fʏ{y}为分布函数F{x,y}的边缘分布函数。