正态分布中的半正定矩阵(协方差矩阵)
1.什么是正定矩阵和半正定矩阵
我们学习半正定矩阵前,得先了解,正定矩阵与半正定矩阵的关系以及什么是正定矩阵。这里先学习什么是二次型。
首先给出二次型的定义
定义1:设P为数域, a i j ∈ P , i , j = 1 , 2 , … , n a_ij∈P,i,j=1,2,…,n aij∈P,i,j=1,2,…,n,n个数字x_1,x_2…,x_n的二次齐次多项式。
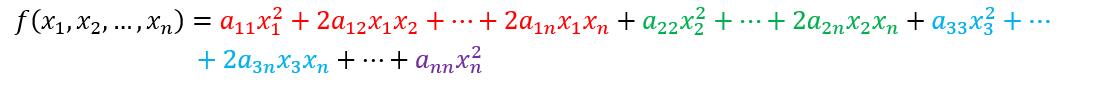
称为数域P上的一个n元二次型
而这个式子可进一步可写成:
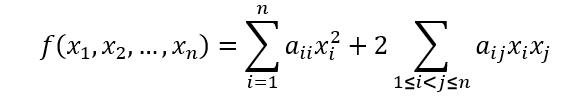
由于约定二次型中
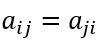
,可知 x i x j = x j x i x_i x_j=x_j x_i xixj=xjxi,有
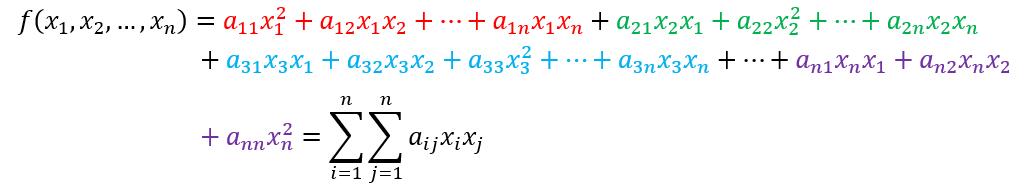
由于笔者数学基础差,在此记录一下转化过程

将上式子的系数a排列成一个n×n矩阵

这个矩阵就称为二次型的矩阵,由于上面我们所约定 a i j = a j i , i , j = 1 , 2 , … , n a_ij=a_ji,i,j=1,2,…,n aij=aji,i,j=1,2,…,n,由此可知 A ′ = A A'=A A′=A。
意思是:转置矩阵=原矩阵
这种转置矩阵和原矩阵相等的矩阵称为对称矩阵,即二次型矩阵都是对称矩阵。
这个式子可以进一步化成以下形式:
原式为:
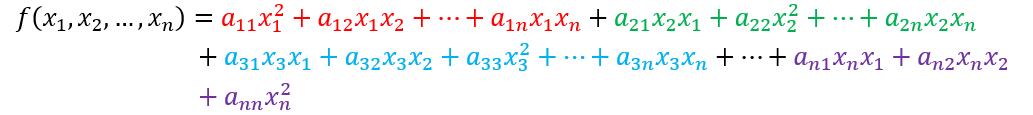
把x提出来
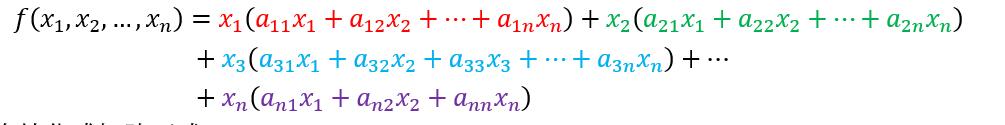
再次转化成矩阵形式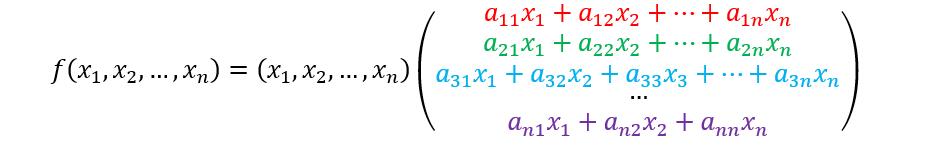
再把矩阵中x提取出来得到
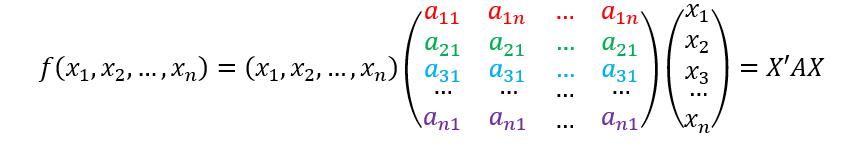
其中

我们称 f(x)=X’AX 为二次型的矩形形式,其中实对称矩阵A称为该二次型的矩阵。
二次型f称为实对称矩阵A的二次型。实对称矩阵A的秩称为:二次型的秩。于是,二次型f与其实对称矩阵A之间有一一对应关系。
∀ x ∈ R n 且 𝑥 ≠ 0 { X T A X > 0 ( 1 ) X T A X ≥ 0 ( 2 ) ∀x∈R^n且𝑥≠0\left\{ \begin{aligned} X^T AX>0 (1) \\ X^T AX≥0 (2) \\ \end{aligned} \right. ∀x∈Rn且x=0{XTAX>0(1)XTAX≥0(2)
其中(1)式成立,则称为正定矩阵,(2)式成立则称为半正定矩阵。
其中x^T Ax为二次型的矩形形式。
举一个简单的例子:
(1)假设
A = [ 1 0 0 1 ] , x = [ x 1 x 2 ] A=\left[ \begin{matrix} 1 & 0 \\0 & 1 \\ \end{matrix} \right], x=\left[ \begin{matrix} x_1 \\x_2\\ \end{matrix}\right] A=[1001],x=[x1x2]
则 X T A X = x 1 2 + x 1 2 > 0 X^T AX=x_1^2+x_1^2>0 XTAX=x12+x12>0。满足这一条件称为正定矩阵。
(2)假设
A = [ 1 1 1 1 ] , x = [ x 1 x 2 ] A=\left[ \begin{matrix} 1 & 1 \\1 & 1 \\ \end{matrix} \right], x=\left[ \begin{matrix} x_1 \\x_2\\ \end{matrix}\right] A=[1111],x=[x1x2]
则 X T A X = x 1 2 + x 1 2 + 2 x 1 x 2 = ( x 1 + x 2 ) 2 ≥ 0 X^T AX=x_1^2+x_1^2+2x_1 x_2=(x_1+x_2 )^2≥0 XTAX=x12+x12+2x1x2=(x1+x2)2≥0。满足这一条件称为半正定矩阵。
2.正定矩阵和半正定矩阵意义
在一维中,二次函数表达形式为
y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c,
当 a > 0 a>0 a>0时,开口向上,凸函数,存在最低点。当 a < 0 a<0 a<0时,开口向下,凹函数,存在最高点。
输入:x 单元(一维下的值)
输出:y 单值(一维下的值)
在多维中,二次函数的输入x数为矩阵形式,例如:
输入: A = [ x 1 x 2 ⋮ x n m ] , 多 元 ( 多 位 下 的 矩 阵 ) A=\left[ \begin{matrix} x_1 \\x_2 \\\vdots\\x_n \end{matrix}m \right],多元(多位下的矩阵) A=⎣⎢⎢⎢⎡x1x2⋮xnm⎦⎥⎥⎥⎤,多元(多位下的矩阵)
输出:y 单值(一维下的值)
这里我们可以得到一个结论,
假设A矩阵为正定矩阵且对称,则所有特征值≥0;
个人总结推导:
当 A A A矩阵为正定时, ∀ x ∈ R n ∀x∈R^n ∀x∈Rn且 x ≠ 0 , X T A X > 0 x≠0,X^T AX>0 x=0,XTAX>0 。
当 A A A矩阵为对称时, A T = A A^T=A AT=A,且必有正交矩阵 P T A P = ∧ P^T AP=∧ PTAP=∧,其中 ∧ ∧ ∧是以 A A A的 n n n个特征值为对角元素的对角矩阵。对应于不同特征值的特征向量正交,故这 n n n个单位特征向量两两正交。以它们为列向量构成正交矩阵P,则可得到: P T A P = P T ∧ P = ∧ P^T AP=P^T∧P=∧ PTAP=PT∧P=∧
即可得: A = P T ∧ P A=P^T∧P A=PT∧P。
将 A = P T ∧ P 代 入 X T A X > 0 A=P^T∧P代入X^T AX>0 A=PT∧P代入XTAX>0,可得: X T P T ∧ P X > 0 X^T P^T∧PX>0 XTPT∧PX>0。
假设 y = P T X , y T = P X T , P T y=P^T X,y^T=PX^T, P^T y=PTX,yT=PXT,PT为一个可逆的n×n矩阵。则 X T P ∧ P T X > 0 X^T P∧P^T X>0 XTP∧PTX>0可化为 y T ∧ y > 0 y^T∧y>0 yT∧y>0。
因为
∧ = [ λ 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ λ 1 ] ∧=\left[ \begin{matrix} λ_1 & \cdots&0 \\ \vdots & \ddots &\vdots \\0&\cdots&λ_1 \end{matrix} \right] ∧=⎣⎢⎡λ1⋮0⋯⋱⋯0⋮λ1⎦⎥⎤
y T ∧ y = λ 1 y 1 2 + λ 2 y 2 2 + ⋯ + λ n y n 2 > 0 y^T∧y=λ_1 y_1^2+λ_2 y_2^2+⋯+λ_n y_n^2>0 yT∧y=λ1y12+λ2y22+⋯+λnyn2>0,可得到当取任取 y i = 1 y_i=1 yi=1,其他元素都为0时,可得到 λ i > 0 λ_i>0 λi>0。
个人理解:对于 x ≠ 0 x≠0 x=0,其 y T ∧ y > 0 y^T∧y>0 yT∧y>0的情况下, y T y^T yT和 y y y都不等于0。且 y T y^T yT和 y y y相乘都为正,所以 ∧ ∧ ∧的值应大于0,即所有的 λ i λ_i λi>0。
同理可推出半正定矩阵中的特征值。
假设 A A A矩阵为半正定矩阵,则所有特征值≥0;
3.半正定矩阵
上面已经介绍了半正定矩阵,下面证明协方差矩阵是半正定矩阵。
首先先理解什么是协方差矩阵
设 Y = [ ( y 1 , y 2 , y 3 , … , y n ) ] T Y=[(y_1,y_2,y_3,…,y_n)]^T Y=[(y1,y2,y3,…,yn)]T为 n n n维随机变量,称矩阵为
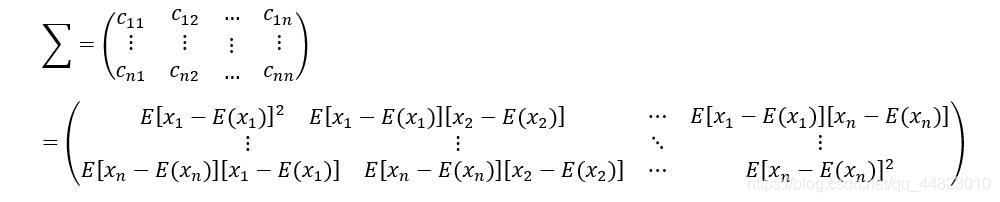
要证明 ∑ ∑ ∑为半正定矩阵,需要证明对于任意 Y = [ ( y 1 , y 2 , y 3 , … , y n ) ] T Y=[(y_1,y_2,y_3,…,y_n)]^T Y=[(y1,y2,y3,…,yn)]T为 n n n维随机变量,有 Y T ∑ Y ≥ 0 Y^T∑Y≥0 YT∑Y≥0。
先计算Y^T∑部分
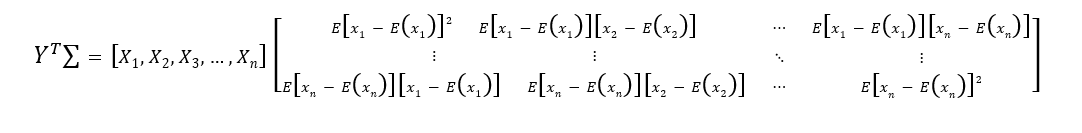
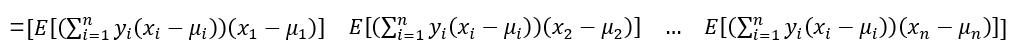
在把 X X X加进去,计算 Y T ∑ Y Y^T∑Y YT∑Y部分
假设
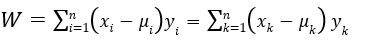
由此我们可以得到: Y T ∑ Y = E ( W 2 ) > 0 Y^T∑Y=E(W^2)>0 YT∑Y=E(W2)>0
所以我们可以理解了在概率机器人中多元正太分布的密度函数:
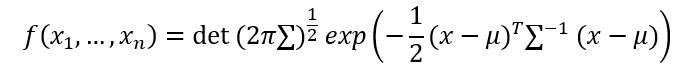
其中,μ数均值矢量,∑是一个半正定矩阵也称协方差矩阵。