1. 爱心第一种

ContourPlot3D[{x^2 + (9 y^2)/4 + z^2 - 1}^3 - x^2 z^3 - (9 y^2 z^3)/80 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, PlotTheme -> "Classic"]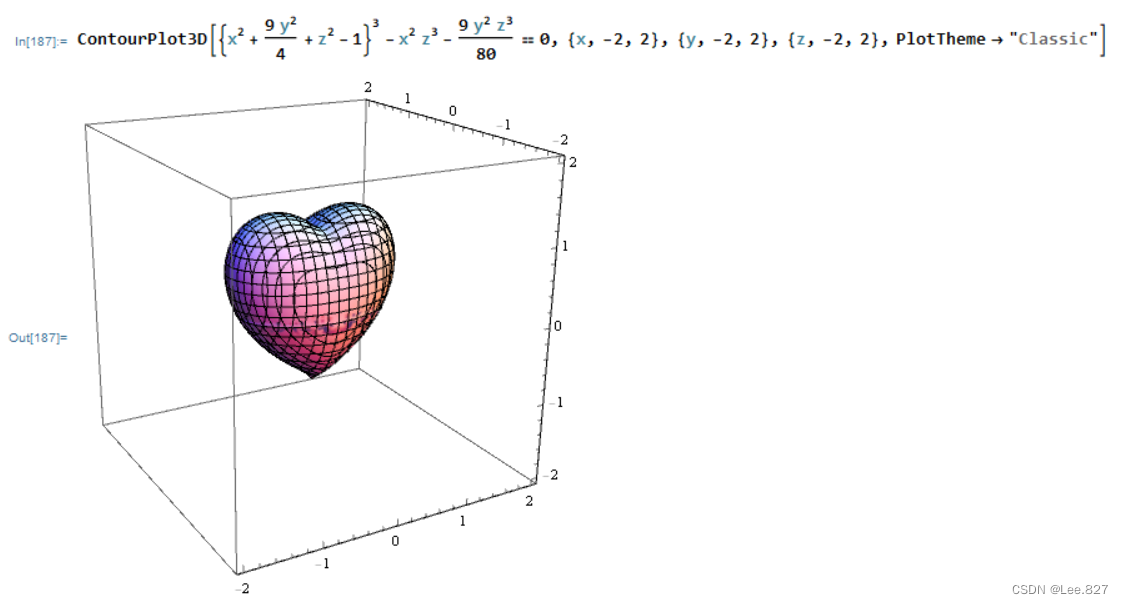

 或更改样式

ContourPlot3D[{x^2 + 9/4*y^2 + z^2 - 1}^3 - x^2*z^3 - 9/80*y^2*z^3 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, ContourStyle -> {Magenta, Specularity[White, 5]}]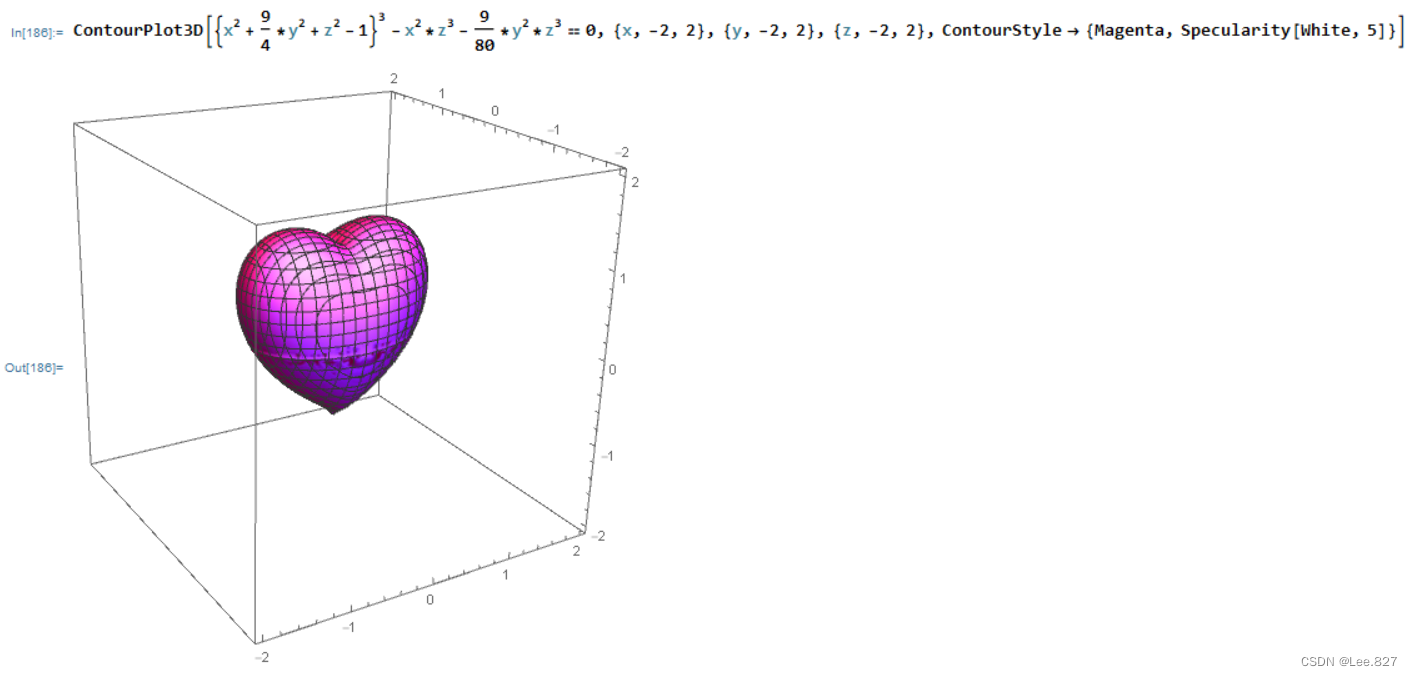

 2. 爱心第二种

ContourPlot3D[(x^2 + 2 y^2 + z^2 - 1)^3 - x^2 z^3 - (y^2 z^3)/10 == 0, {x, -1.3, 1.3}, {y, -1, 1}, {z, -1.3, 1.3}, PlotPoints -> 100, BoxRatios -> Automatic, Mesh -> None, Axes -> False, ContourStyle -> {Magenta, Specularity[White, 5]}]

 3. 爱心第三种

f[x_] := Sqrt[1 - (Abs[x] - 1)^2]
g[x_] := ArcCos[1 - Abs[x]] - 3
p1 = Plot[{f[x], g[x]}, {x, -3, 3}, PlotRange -> {{-5, 5}, {-4, 4}}, GridLines -> {Range[-4, 4], Range[-4, 4]}, PlotStyle -> Directive[RGBColor[1., 0.17, 0.3], Opacity[1.], AbsoluteThickness[2.]], Filling -> {1 -> {2}}];
p2 = Graphics[{Text[Style["MATHEMATICS", Bold, 25, FontFamily -> name], {0, -1}], Text[Style["f(x)=\!\(\*SqrtBox[\(1 - \*SuperscriptBox[\((\
\[LeftBracketingBar]x\[RightBracketingBar] - 1)\), \(2\)]\)]\)", 10, FontFamily -> name], {3, 3.25}],Text[Style["g(x)=arccos(1-\[LeftBracketingBar]x\[RightBracketingBar])-3", 10, FontFamily -> name], {3, 2.5}]}];
Show[p1, p2]

 // 非本人原创代码，参考来源知乎等