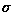缓存是计算机科学中可以提高系统性能的最基本、最有效的一种方法之一。当完整的数据不适合全部缓存时，通过将一小部分数据存放到更快、更接近应用程序的内存中来提高性能。缓存可以提高性能的最直观原因在于数据的访问都表现出相当程度的“局部性”。更正式的表征这种“局部性”的方式，是通过概率分布来描述所有可能的数据项访问频率，在许多计算机科学的领域内，这种概率都表现出高度偏斜，也就是说少数的数据项会比其他数据项更可能被访问。并且在非常多的场景中，访问模式和概率分布会随着时间而变化，这种现象被称为“时间局部性”。

当访问一个数据项时，如果它已经在缓存中，我们称之为缓存命中。否则，成为缓存未命中。缓存命中的次数和数据项访问的总次数之间的比值，称为缓存命中率。因此，如果保存在缓存中的数据项对应为访问频率最高的数据项，那缓存一般都会有比较高的命中率。

缓存的大小一般都会受限，那么缓存的设计人员面临着选择哪些数据项保存到缓存中的难题。特别是，当缓存已经满的的时候，需要决定把哪些数据项移除缓存。显然，这种移除的策略一定要做到高效，以避免出现以下的情况：为了做到缓存移除而带来的时间、空间的开销超过了缓存本身带来的性能提升。在缓存中用来确定哪些数据项可以被缓存、哪些数据项被移除的辅助空间，被称为缓存的元数据。在许多的缓存方案中，处理元数据的时间复杂度和元数据的空间大小一般都和缓存中数据项数量成正比。

当数据访问的概率分布随时间的变化是恒定的时候，Least Frequently Used（LFU）是缓存命中率最高的。因为在大小为n的LFU缓存中，保存的一定是n个访问频率最高的数据项。但是LFU有两个问题，首先，LFU需要维护复杂、大量的元数据。其次，在大多数的实际场景中，访问频率会随着时间发生根本的变化。例如：视频缓存服务，在某一天突然非常流行的视频剪辑，在几天后可能都不会再被访问。因此一个数据项不能因为曾经的高频率访问而继续被保留在缓存中。

于是也产生了很多LFU的代替方案。这些方案很多都利用了衰减机制或者限制采样最后w次访问的窗口机制。这种衰减机制一方面是为了限制元数据的大小，一方面是为了缓存和淘汰机制可以更适应于最近流行的数据项。一个比较经典的实现方案叫做WLFU。并且，在绝大多数的情况下，新访问的数据项都会被插入到缓存中，而缓存方案只关注于如何淘汰数据，因为维护不在缓存中数据项的元数据，是不切实际的。

维护历史所有访问过的数据项元数据的代价是非常昂贵的，一般的LFU都只会维护缓存中存在的数据项元数据。因此，一般把前者称为Perfect LFU（PLFU），将后者称为In-Memory LFU来区分它们。

依赖于“时间局部性”的一种替代LFU的缓存方案叫做LRU，LRU中最近被访问的数据项都会被插入缓存，而当缓存满时，最久未被访问的会被淘汰。相比于LFU，LRU的性能会更高，而且自动适应数据的时间局部性，并且可以应对数据的突发流量。但是在实际的场景中，LRU需要更大的缓存空间，才能和LFU达到相同的缓存命中率。

tinyLFU的体系结构如下图所示，当有新数据插入时，缓存淘汰策略选定一个候选淘汰数据项，tinyLFU来决定是否用新的数据项来代替候选被淘汰数据项，来增加缓存命中率。

因此，tinyLFU需要维护相当长的一段历史时期内数据项访问的频率统计信息。维护这一份数据的代价是相当昂贵的，所以tinyLFU面临着两个挑战，首先是需要维护一个新鲜度机制，目的是保持历史记录的访问记录，并且可以移除旧的数据项。其次是内存的优化，因为维护历史数据项的频率统计信息，非常耗费内存。

Approximate Counting

计数布隆过滤器（CBF）是布隆过滤器的一种，其向量不在表述为单个位，而是一个计数器。在插入数据时，不再是标记位，而是要增加对应索引的计数。最小增量CBF是一种增强的计数布隆过滤器，它支持两种方法：加法和预估。

预估：通过计算key的多个hash值，把这些hash作为索引，读取每个索引位置的计数器的值，把其中最小的值作为预估返回结果。

加法：同样计算key的多个hash值，并且读取每个索引位置的计数器的值，但是只会增加其中数值最小的计数器的值。

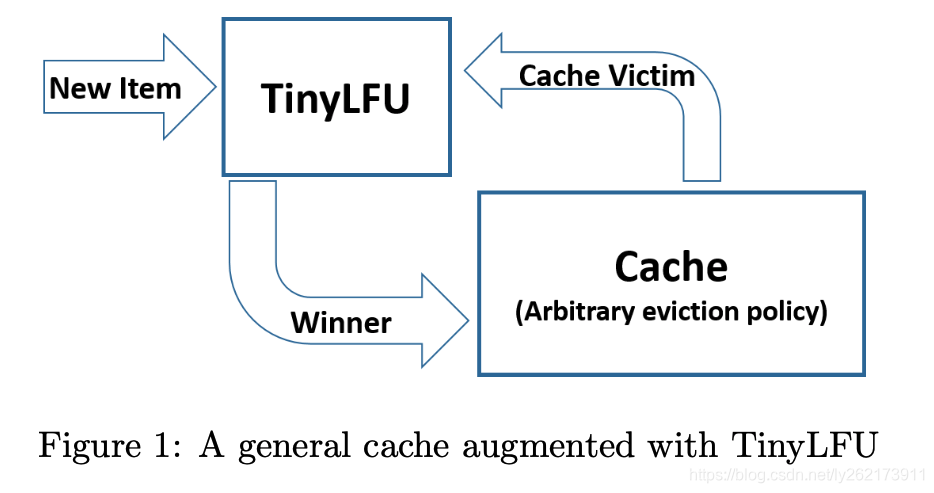
例如下图，我们使用三个哈希函数，对于一个新访问的数据x，我们通过哈希函数得到三个值（2，2，5），当插入这个数据x时，只会对最小的两个计数值2加到3，而5的计数器不变。

 

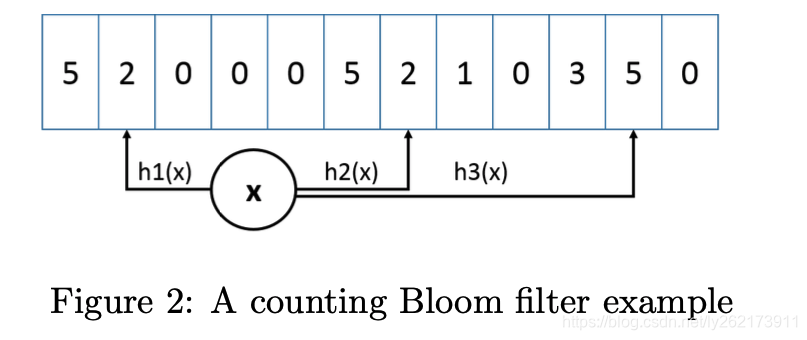
仅对于最小的计数器增加，是可以避免对于大计数器的不必要的增加，这样可以更好地对高频的数据项进行评估，因为一般情况下，这种低频数据项，很难把计数器增加到很高的程度。

Freshness Mechanism

为了维持CBF的新鲜，（这里我的理解为，如果一直累加数据，会导致数据的历时性较强，为了可以让最近的数据有机会插入到缓存中，需要对这些历史性做一些清理，即保持新鲜），文章提出了一种rest机制，即每当有新的元素添加到CBF中，都会对一个计数器增加一个数值，当这个数值到达我们预设的阈值时，会对CBF中维护的所有计数器的数值除以2。这里有两个有趣的地方：第一，维护一个计数器不会占用太多空间，只是会占用log(w)的位空间。第二，这种做法提高了高频数据的准确性。因为可以通过不断地扩充空间大小，来提高预估值的精确性，这篇文章证明了reset操作降低了空间成本，并且在相同的空间下，拥有更精确的预估值。

下面的证明过程就省略了。主要指导作者对于reset操作的正确性和更精确性，是有数学理论证明的。

但是由于reset采用了整数除法，所以会有截断误差，最坏情况下，截断后的值要比理论值小1。样本数据越大，截断误差带来的影响越小。

Doorkeeper

因为实际场景中通常会有一些长尾流量，如果对于这些长尾流量我们都要进行计数器的计数，那大多数的计数器都会被这些只访问一次的长尾流量占用。为了减少这部分数据项的影响，减少计数器的大小，又提出了Doorkeeper机制。即在CBF前增加了一个常规的布隆过滤器。当有新的数据项插入时，如果该数据项在Doorkeeper中，则直接插入到CBF主结构中。如果不存在，则只插入到Doorkeeper中。当访问数据项时，会同时查询Doorkeeper和主结构，当该数据项在Doorkeeper中时，该数据项的预估值等于tinyLFU主结构计算出来的预估值加1。否则就等于主结构预估值。

每次reset操作时，都会清空Dookeeper。

这样每个reset周期，都会清除只访问一次的数据项。但是这种清除同样也会对数据频率的预估值降低1，带来一些误差。

The W-TinyLFU Optimization

W-tinyLFU是在Caffeine Java开源库里的一种优化实现，因为tinyLFU是无法应对突发流量的，因为这些突发流量是无法在构建足够大的频率以驻留在缓存中。

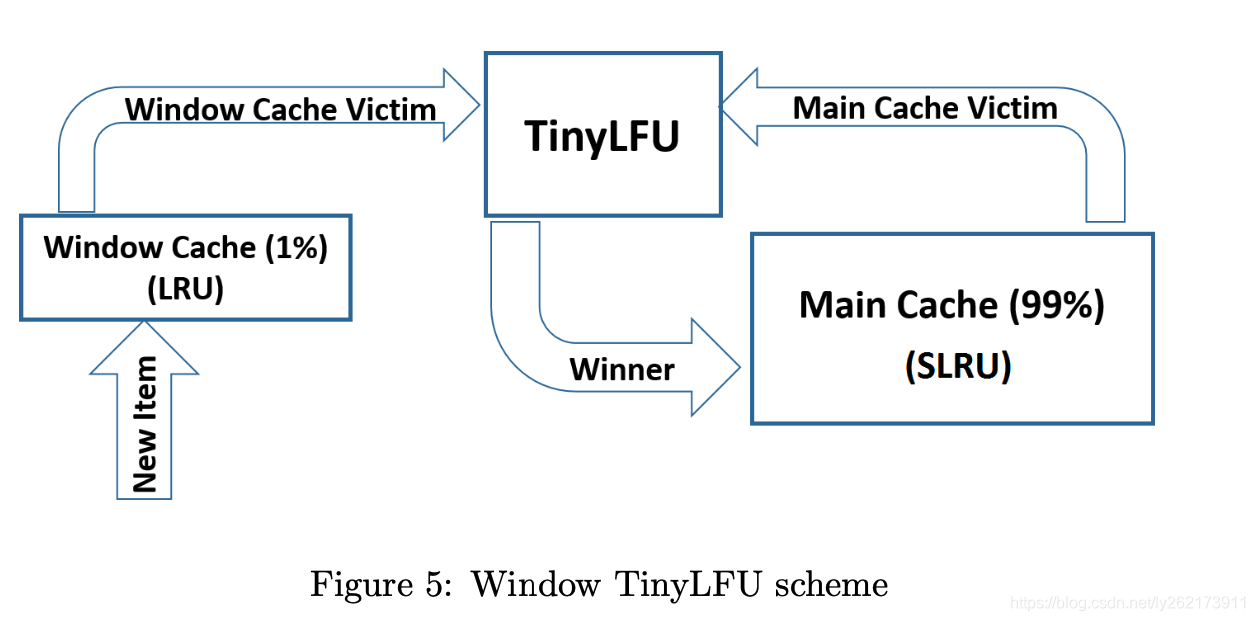
整个缓存结构被分为两部分，主缓存利用SLRU淘汰策略和tinyLFU接纳策略，即tinyLFU会根据CBF中的历史数据预估值和被淘汰数据的频率作比较，保留较大的，来达到更高的命中率。window缓存只使用LRU淘汰策略。主缓存分为了A1和A2区域，A2占用80%的空间缓存热数据，A1占20%的空间缓存冷数据，当需要淘汰时，从A1中选择数据项。

任何新的数据，都是会被保存到window缓存的，并且window缓存被淘汰的数据是有机会进入到主缓存的。如果被接受，那整个缓存最终被淘汰可能就是主缓存中A1区域的数据。

 

总结下：该文章提出的W-tinyLFU有以下几点非常好的思想：

1.reset机制，一方面让数据的缓存有了时间局部性的特性，一方面也降低了内存的消耗。

2.doorkeeper机制，避免了长尾流量的影响。

3.window cache的机制，让突发流量有了被缓存的可能性，提高了缓存的命中。

4.CBF，作为一种预估值，是可以证明其实际值与预估值的差距是不会很大的，并且用很小的空间代价，保存了很长的历史数据的统计数据，给tinyLFU的接纳策略提供了数据基础。

公众号：