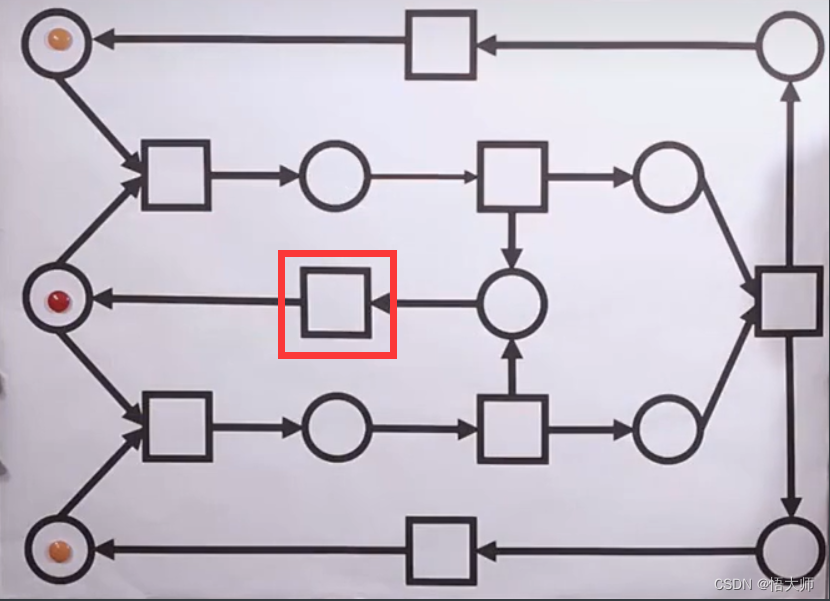
petri网

2、有向网

三元组 $N=(S,T;F)$ 称为有向网，如果

表达式	含义
$S\bigcup T\ne \varnothing$	非空
$\bigwedge S\bigcap T\ne \varnothing$	两类元素
$\bigwedge F\subseteq S\times T\bigcup T\times S$	两种关系
$\bigwedge dom(F)\bigcup cod(F)=S\bigcup T$	无孤立元素

其中：

• d o m ( F ) = { x ∣ ∃ y : ( x , y ) ∈ F } dom(F) = \{x| \exists y:(x,y)\in F \} dom(F)={x∣∃y:(x,y)∈F}
• c o d ( F ) = { y ∣ ∃ x : ( x , y ) ∈ F } cod(F) = \{y| \exists x:(x,y)\in F \} cod(F)={y∣∃x:(x,y)∈F}

例1：

• S = { c , x , q , d } S=\{c,x,q,d\} S={c,x,q,d}
• T = { c x , x q , q d , d c } T=\{cx,xq,qd,dc\} T={cx,xq,qd,dc}
• $F=\{(c,cx),(cx,x),(x,xq),(xq,q),(q,qd),(qd,d),(d,dc),(dc,c)\}$
• N 1 = { S , T ; F } N_1=\{S,T;F\} N1​={S,T;F}
• 

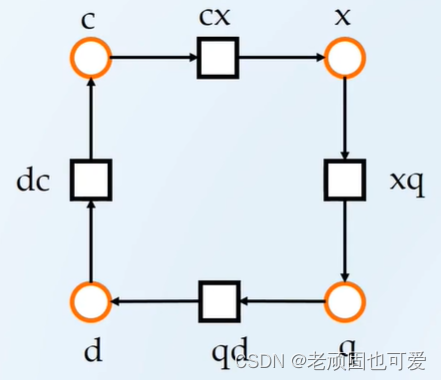
例2：

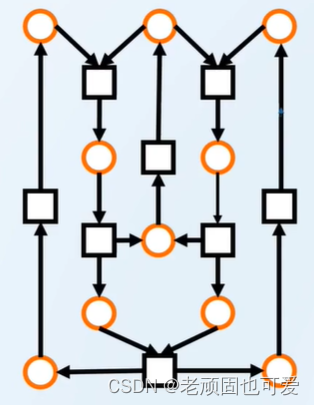
2.1 基本元素

• $S$ 元素： place 库所
• $T$ 元素：transition 变迁（不是迁移，不只是搬家，这个既有质变，又有量变)
• F：flow relation 流关系

2.2 表达方式比较

• 半形式化定义：易读，适合书面交流
• 形式化定义：适合引入数学方法，便于自动处理
• 图形表示：直观 便于交流，突显网状结构，面对面交流时无须为元素命名

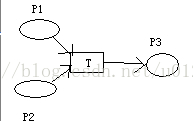
例3：

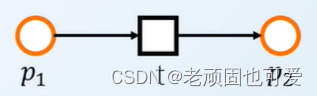
• 上图是 N = ( { S 1 , S 2 } , { t } ; { ( S 1 , t ) , ( t , S 2 ) } ) N=(\{S_1,S_2\},\{t\};\{(S_1,t),(t,S_2)\}) N=({S1​,S2​},{t};{(S1​,t),(t,S2​)}) 的图形表示吗？
• 在同构的意义上，是（同构：同类元素之间的一一对应，包括 $F$ ）

例4：

• 这是一个有向网吗？
• 可以看成一个，也可以看成两个。定义没有明确规定是否联通。
• 但是，既然两部分没有联系，为什么要放在一起研究？这就要从实际应用触发。

2.3 连通性

• 
  弱连通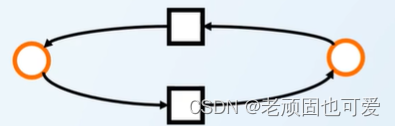
• 
  强连通，去掉一条边还连通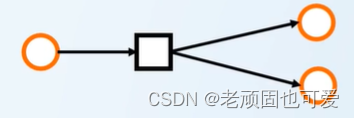
• 
  不连通，最后两个无连接

2.4 单纯网、简单网

有向网允许以下结构吗？

• 
  不单纯（单纯性)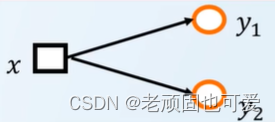
• 
  不简单（简单性)
• 
  重复弧，不能出现

2.4.1 术语：前集、后集

$X=S\bigcup T$ 有向网的节点集合元素集
x , y ∈ X f ( x ) = { . x = { y ∣ ( y , x ) ∈ F } , x 的前集 x . = { y ∣ ( x , y ) ∈ F } , x 的后集 x,y \in X \\ f(x)=\left\{ \begin{aligned} ^.x & = & \{y|(y,x)\in F\} & , &x的前集 \\ x^. & = & \{y|(x,y)\in F\} & , &x的后集 \end{aligned} \right. x,y∈Xf(x)={.xx.​==​{y∣(y,x)∈F}{y∣(x,y)∈F}​,,​x的前集x的后集​

2.4.2 单纯网、简单网、连通网

2.4.2.1 单纯网定义

$$\begin{gathered} \forall x\in X:{ \\ }^{.}x\cap x^{.}\ne \varnothing \end{gathered}$$

2.4.2.2 简单网定义

$$\begin{gathered} \forall x,y\in X:{ \\ }^{.}x{=}^{.}y\bigwedge x^{.}=y^{.}\bigwedge x\ne y \end{gathered}$$

2.4.2.3 连通图定义

$$\begin{gathered} \forall x,y\in X: \\ (x,y)\in (F\cup F^{-1}{)}^{+} \\ 其中F^{-1}=\{(a,b)|(b,a)\in F\} \end{gathered}$$

2.4.2.4 重复弧问题

不允许重复弧

2.4.2.5 对偶网和互逆网

$$\begin{gathered} N=(S,T;F),N^{\prime }=(S^{\prime },T^{\prime };F^{\prime })为有向网 \\ N和N^{\prime }为对偶网,如果S^{\prime }=T\bigwedge T^{\prime }=S\bigwedge F^{\prime }=F \\ N和N^{\prime }为互逆网,如果S^{\prime }=S\bigwedge T^{\prime }=T\bigwedge F^{\prime }=F^{-1} \end{gathered}$$

以下两个网是同一个网，同为 N = ( { S 1 , S 2 } , { t } ; { ( S 1 , t ) , { t , S 2 } } ) N=(\{S_1,S_2\},\{t\};\{(S_1,t),\{t,S_2\}\}) N=({S1​,S2​},{t};{(S1​,t),{t,S2​}}) 的图示

2.4.3 有限网 & 无限网

有向网可有有限多个元素，也可以有不可数的有限多个元素 $|S\cup T|<\infty$

• 有限网
  • 人造系统：能力有限
  • 自然规律（如四季变化）：局部观察
• 无限网
  • 记录无始无终的自然变化
  • 理论研究（图灵机）

2.5 出现网

把出现的现象记录下来

例5：

2.6 基础概念定义金律

没有必要包含的,就有必要不包含

2.6.1 有向网定义不包含

• 连通性
• 单纯性
• 简洁性
• 有限性

2.6.2 有向网概念特点

• 基础概念简洁
• 可灵活引入后续概念