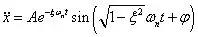课程《生物数据处理》 老师:邓阳君老师
要求:请采用 k 均值 、 k 中心点、层次聚类或者模糊聚类等对 iris 数据 进行聚类分析,
并评价其效果。实验报告应包括算法理论知识、算法代码、仿真实验结果及其分析等内
容,请于 5 月 31 日前提交实验报告。
一、算法理论知识
聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程,聚类就是一种发现这种内在结构的技术,聚类技术经常被称为无监督学习。
k 均值聚类是最著名的划分聚类算法,由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目 k,k 由用户指定,k 均值算法根 据某个距离函数反复把数据分入 k 个聚类中。
(1)K 均值聚类算法
K-means 算法也称为 K_ 均值算法,用于聚类算法。聚类是一种无监督学习,他将相
似的对象归于一个簇中,簇中心通过簇中所有点的均值来计算。聚类算法与分类算法的
主要区别就是分类的目标类别已知,而聚类的目标类别未知。
簇:所有数据点的点集合,簇中的对象是相似的
质心:簇中所有点的中心(由簇中所有点的均值求得)
SSE:Sum of Sqared Error 平方误差和,SSE 越小表示越接近质心
(2)算法原理
误差平方和 SSE 用来衡量 K-means 算法的好坏
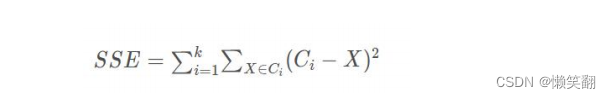
C 为聚类中心,X 为簇中数据点
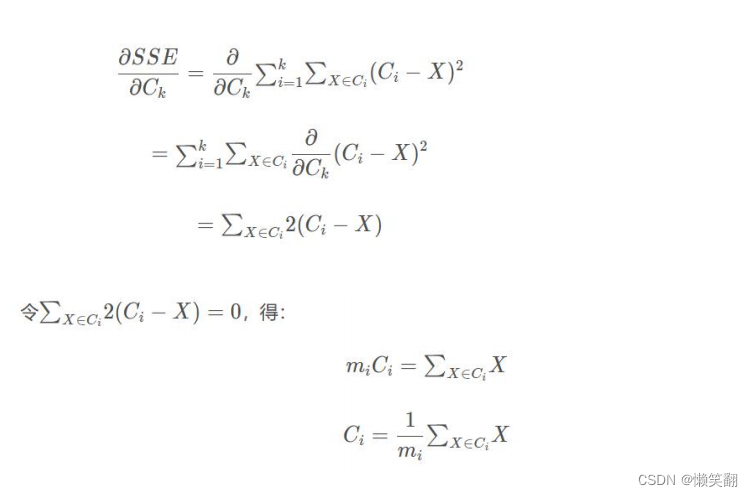
由推导可以看出,当质心为簇中数据均值时,SSE 最小
(3)K-Means 算法步骤
1. 从数据中选择 k 个对象作为初始聚类中心;
2. 计算每个聚类对象到聚类中心的距离来划分;
3. 再次计算每个聚类中心
4. 计算标准测度函数,直到达到最大迭代次数,则停止,否则,继续操作。
5. 确定最优的聚类中心
(4)性质
k 均值聚类是使用最大期望算法(Expectation-Maximization algorithm)求解的 高斯混合模型(Gaussian Mixture Model, GMM)在正态分布的协方差为单位矩阵,且 隐变量的后验分布为一组狄拉克δ函数时所得到的特例。
二、算法代码
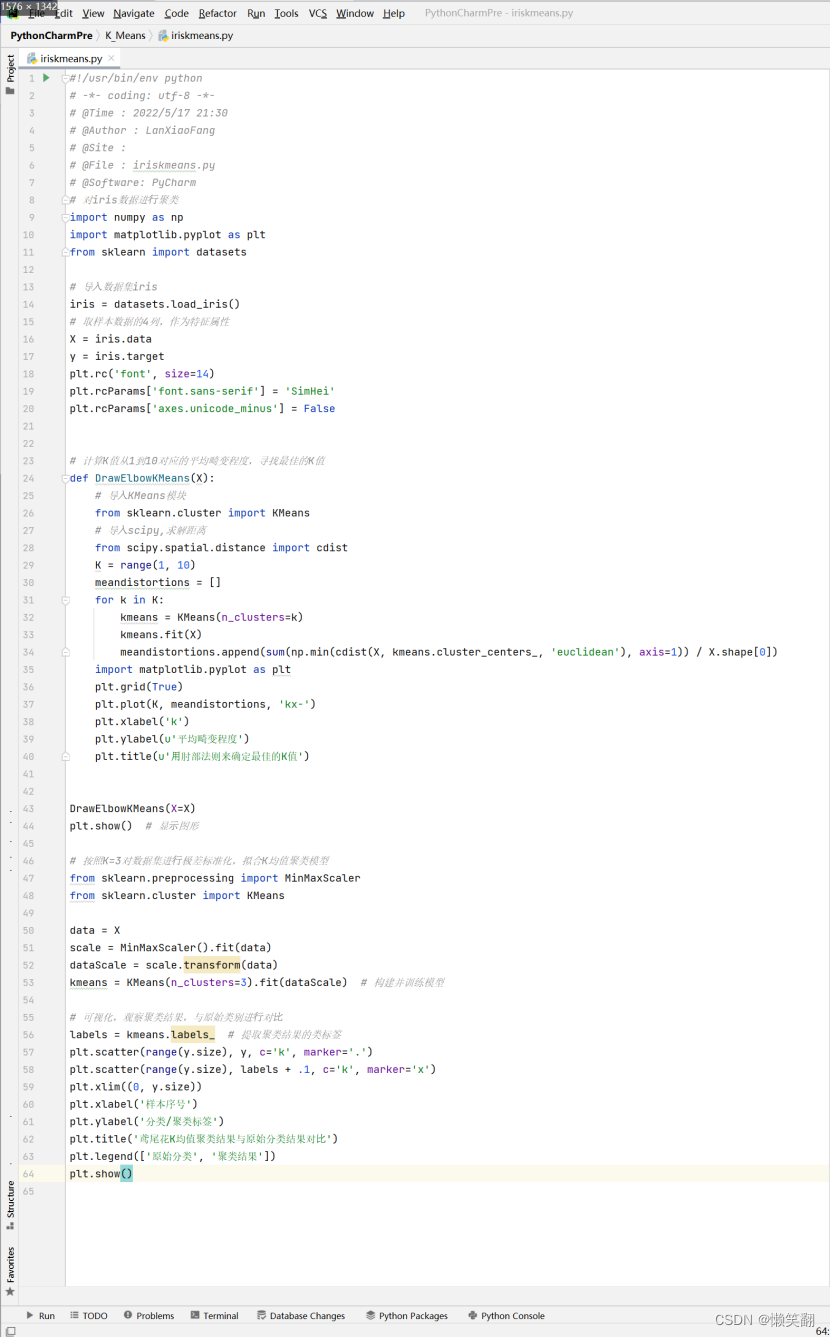
三、仿真实验结果及其分析
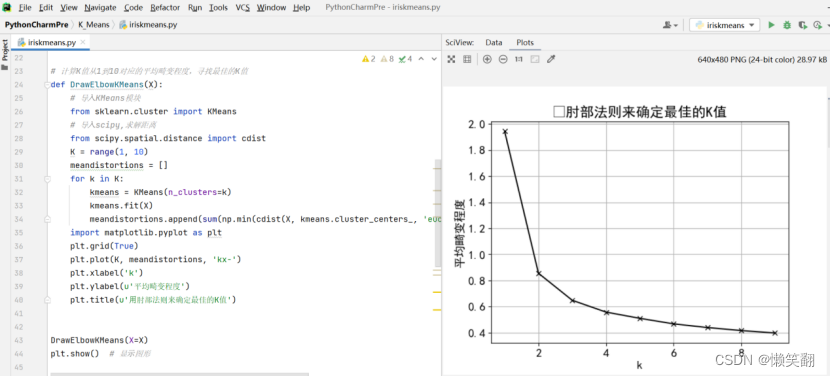
图 1 从图中可知,较好的K值为2或3
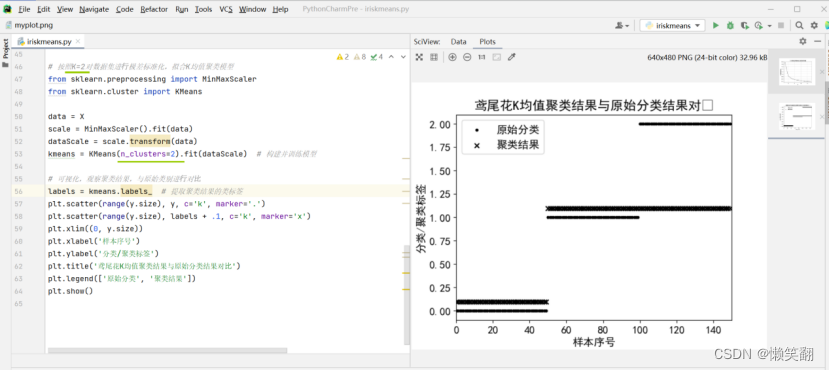
图 2 k=2时
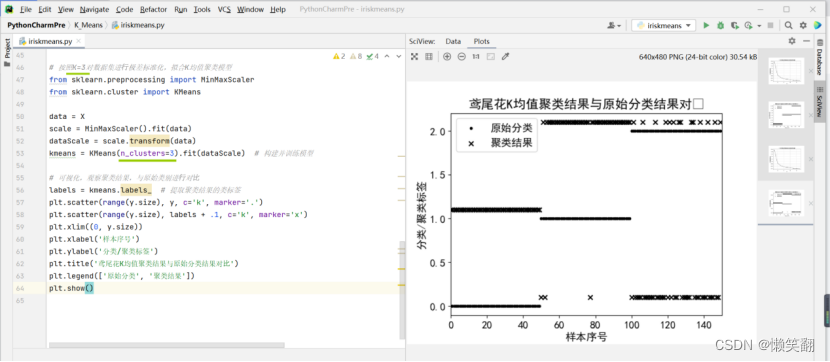
图 3 k=3时
学习总是没有止境的,就如同K值拐点的选择一样,人生也并不是唯一确定的,人生不同之处在于,数据有最佳选择,但是人生永远没有最好的选择,我们能做的就是把选择的路走到最好。共勉~在学习的路上,新手上路总会磕磕碰碰,但是我们要迎难而上,就像学走路时的你,不就是跌跌撞撞学会的走路吗?人生是个圆,有的人走了一辈子也没有走出命运画出的圆圈,他就是不知道,圆上的每一个点都有一条腾飞的切线。希望自己能认真努力的把握机会,就算没有机会,也要创造机会,达到自己的奋斗目标。