03 数字图像技术——频域滤波实验结果与分析——python

article/2025/5/14 2:04:13

04 数字图像技术——图像特征提取之实验结果与分析
03 数字图像技术——频域滤波实验结果与分析
02 数字图像技术——颜色空间转换与颜色空间分割实验结果与分析
01 数字图像基本操作——图像采样、量化、算术运算、点运算实验结果及分析

一、实验目的

1．了解图像变换的意义和手段；
2．熟悉傅里叶变换的基本性质；
3．熟练掌握FFT变换方法及应用；
4．通过实验了解二维频谱的分布特点；
5．通过本实验掌握利用python编程实现数字图像的傅里叶变换。

二、实验内容

1. 实现数字图像的FFT变换。
2. 掌握图像FFT变换的性质。
3. 图像FFT变换的性质体现规律和特点分析。
4. 实现低通滤波器。

三、实验设备/仪器

电脑、编程语言(Matlab或Python)、图像数据和存储器。

四、实验原理

1．应用傅里叶变换进行图像处理
  傅里叶变换是线性系统分析的一个有力工具，它能够定量地分析诸如数字化系统、采样点、电子放大器、卷积滤波器、噪音和显示点等的作用。通过实验培养这项技能，将有助于解决大多数图像处理问题。对任何想在工作中有效应用数字图像处理技术的人来说，把时间用在学习和掌握博里叶变换上是很有必要的。
2．傅里叶（Fourier）变换的定义
对于二维信号，二维Fourier变换定义为：
在这里插入图片描述

逆变换：
在这里插入图片描述

二维离散傅里叶变换为：
在这里插入图片描述

逆变换：
在这里插入图片描述

  图像的傅立叶变换与一维信号的傅立叶变换变换一样，有快速算法，具体参见参考书目，有关傅立叶变换的快速算法的程序不难找到。实际上，现在有实现傅立叶变换的芯片，可以实时实现傅立叶变换。

五、实验步骤与要求

  1. 编写python代码，实现一维信号的傅里叶变换；
  2. 编写python代码，实现图像的二维傅里叶变换；
  3. 编写python代码，实现理想低通滤波器；
  4. 编写python代码，实现巴特沃斯低通滤波器。
  5. 记录和整理实验报告。

六、各实验流程图、结果及分析

1. 编写python代码，实现一维信号的傅里叶变换；
在这里插入图片描述

图 1 基于傅里叶变换的数字图像频域处理过程

在这里插入图片描述

图 2 一维信号的傅里叶变换流程图

代码如下：

import matplotlib.pyplot as plt
import numpy as np
"""中文显示工具函数"""
def set_ch():from pylab import mplmpl.rcParams['font.sans-serif']=['FangSong']mpl.rcParams['axes.unicode_minus']=False
set_ch()
def show(ori_func, ft, sampling_period = 5):n = len(ori_func)interval = sampling_period / n# 绘制原始函数plt.subplot(2, 1, 1)plt.plot(np.arange(0, sampling_period, interval), ori_func, 'black')plt.xlabel('时间'), plt.ylabel('振幅')plt.title('原始信号')# 绘制变换后的函数plt.subplot(2,1,2)frequency = np.arange(n / 2) / (n * interval)nfft = abs(ft[range(int(n / 2))] / n )plt.plot(frequency, nfft, 'red')plt.xlabel('频率 (Hz)'), plt.ylabel('频率谱')plt.title('傅里叶变换结果')plt.show()#生成频率为 1（角速度为 2 * pi）的正弦波
time = np.arange(0, 5, .005)
x = np.sin(2 * np.pi * 1 * time)
y = np.fft.fft(x)
show(x, y)
x2 = np.sin(2 * np.pi * 10 * time)
x3 = np.sin(2 * np.pi * 40 * time)
x+=x2+x3
y = np.fft.fft(x)
show(x, y)

在这里插入图片描述

图 3 单一正弦波傅里叶变换结果

在这里插入图片描述

图 4 3个正弦波形叠加的傅里叶变换结果

  从图中可以看出，这三个正弦波形进行叠加得出的图像都具备了各自波形的特点，当进行傅里叶变化时，每个基函数都是一个单频率谐波。

2. 编写python代码，实现图像的二维傅里叶变换；
在这里插入图片描述

图 5 二维傅里叶变换流程图

代码如下：

from skimage import data,io,color
import numpy as np
from matplotlib import pyplot as plt
import cv2 as cv
"""中文显示工具函数"""
def set_ch():from pylab import mplmpl.rcParams['font.sans-serif']=['FangSong']mpl.rcParams['axes.unicode_minus']=False
set_ch()
# img = data.camera()
#img = io.imread('D:\shuzi_image\cat.jpg')
img = cv.imread('D:\shuzi_image\cat.jpg')
img=color.rgb2gray(img)
f = np.fft.fft2(img) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 默认结果中心点位置是在左上角，转移到中间位置
fimg = np.log(np.abs(fshift)) # fft 结果是复数，求绝对值结果才是振幅
# 展示结果
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('原始图像')
#plt.subplot(122), plt.imshow(fimg, 'gray'), plt.title('傅里叶频谱')
plt.subplot(122)
fimg=fimg.astype(np.uint8)
cv.namedWindow('image')
cv.imshow("image",fimg*23)
cv.waitKey()
plt.show()

当默认结果中心点位置是在左上角时，结果如下：
在这里插入图片描述

图 6 图像的二维傅里叶变换结果

默认结果中心点位置是在左上角，转移到中间位置时的结果如下：
在这里插入图片描述

图 7 图像的二维傅里叶变换结果

  可得到：变换之后的图像在原点平移之前四角是低频，最亮，平移之后中间部分是低频，最亮，亮度大说明低频的能量大。
棋盘图像对应的傅里叶变换代码如下： 
from skimage import data
import numpy as np
from matplotlib import pyplot as plt
"""中文显示工具函数"""
def set_ch():from pylab import mplmpl.rcParams['font.sans-serif']=['FangSong']mpl.rcParams['axes.unicode_minus']=False
set_ch()img = data.checkerboard()
f = np.fft.fft2(img) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 默认结果中心点位置是在左上角，转移到中间位置
fimg = np.log(np.abs(fshift)) # fft 结果是复数，求绝对值结果才是振幅
# 展示结果
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('原始图像')
plt.subplot(122), plt.imshow(fimg, 'gray'), plt.title('傅里叶频谱')
plt.show()

在这里插入图片描述

图 8 棋盘图像的傅里叶变换结果

使用两次一维傅里叶变换代替二维傅里叶变换的代码如下：

from matplotlib import pyplot as plt
import numpy as np
from skimage import data, color,io
import cv2 as cv# 中文显示工具函数
def set_ch():from pylab import mplmpl.rcParams['font.sans-serif'] = ['FangSong']mpl.rcParams['axes.unicode_minus'] = Falseset_ch()
img1 = io.imread('D:\shuzi_image\cat.jpg')
img = color.rgb2gray(img1)
# 在X方向实现傅里叶变换
m, n = img.shape
fx = img
for x in range(n):fx[:, x] = np.fft.fft(img[:, x])
for y in range(m):fx[y, :] = np.fft.fft(img[y, :])
# 默认结果中心点位于左上角，转移到中间位置
fshift = np.fft.fftshift(fx)
# fft结果是复数，求绝对值结果才是振幅
fimg = np.log(np.abs(fshift))# 展示结果
plt.subplot(121), plt.imshow(img1, 'gray'), plt.title('原始图像')
plt.subplot(122), plt.imshow(fimg, 'gray'), plt.title('两次一维傅里叶变换的图像')
plt.show()

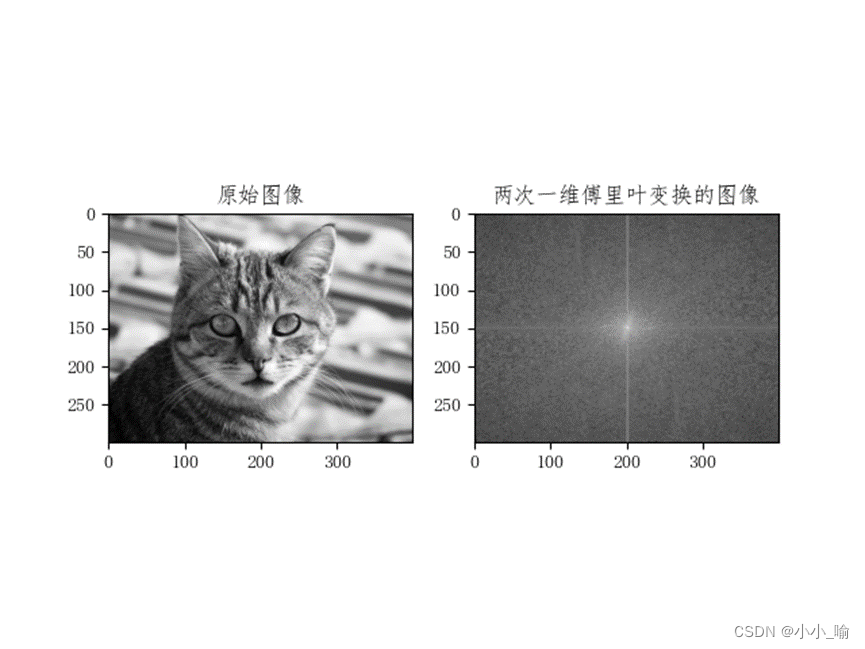
在这里插入图片描述

图 9 使用两次一维傅里叶变换代替二维傅里叶变换的结果

  分析:图像经傅里叶变换后，直流分量与图像均值成正比，高频分量则表明了图像中目标边缘的强度及方向。二维离散傅里叶变换，可视为由沿着x、y方向的两个一维傅里叶变换所构成。这一性质可有效降低二维傅里叶变换的计算复杂性，而且得到效果和一般图像的二维傅里叶变换结果一样。

3. 编写python代码，实现理想低通滤波器；
在这里插入图片描述

图 10 实现理想低通滤波器流程图

代码如下：

#导入相关库
from skimage import data,color,io
import numpy as np
import matplotlib.pyplot as plt
import cv2 as cv
"""中文显示工具函数"""
def set_ch():from pylab import mplmpl.rcParams['font.sans-serif']=['FangSong']mpl.rcParams['axes.unicode_minus']=False
set_ch()D=10
#读入图片
#new_img=data.coffee()new_img = io.imread('D:\shuzi_image\cat.jpg')
new_img=color.rgb2gray(new_img)#numpy中的傅里叶变化
f1=np.fft.fft2(new_img)
f1_shift=np.fft.fftshift(f1)
#np.fft.fftshift()函数来实现平移,让直流分量在输出图像的重心#实现理想低通滤波器
rows,cols=new_img.shape
crow,ccol=int(rows/2),int(cols/2) #计算频谱中心
mask=np.zeros((rows,cols),np.uint8) #生成rows行cols的矩阵，数据格式为uint8
for i in range(rows):for j in range(cols):if np.sqrt(i*i+j*j)<=D:# 将距离频谱中心小于D的部分低通信息 设置为1，属于低通滤波mask[crow - D:crow + D, ccol - D:ccol + D] = 1# img = np.zeros((200, 200), dtype = np.uint8)  #创建黑色空白图像
# img[50:150, 50:150] = 255   # 图像中央放置白色方块f1_shift=f1_shift*mask
cv.imshow("mask",mask*255)
cv.waitKey(0)
#傅里叶逆变换
f_ishift=np.fft.ifftshift(f1_shift)
img_back=np.fft.ifft2(f_ishift)
img_back=np.abs(img_back)
img_back=(img_back-np.amin(img_back))/(np.amax(img_back)-np.amin(img_back))#plt.figure(figsize=(15,8))
plt.figure()
plt.subplot(121),plt.imshow(new_img,cmap='gray'),plt.title('原始图像')
plt.subplot(122),plt.imshow(img_back,cmap='gray'),plt.title('滤波后图像')
plt.show()

当截断频率D设置为100时：

在这里插入图片描述
在这里插入图片描述

图 11 截断频率为100时的理想低通滤波器结果

当截断频率D设置为10时：

在这里插入图片描述
在这里插入图片描述

图 12 截断频率为10时的理想低通滤波器结果

  从实验可以看出当截断频率D设置得越大时，中心频谱的范围越大，即更多的频率分量可以完全无损的通过，图像越清晰。当D设置得越小时，滤波后的图像越模糊。

4. 编写python代码，实现巴特沃斯低通滤波器。
在这里插入图片描述

图 13 实现巴特沃斯低通滤波器流程图

代码如下：

import numpy as np
import matplotlib.pyplot as plt
import numpy as np
from skimage import data,color,ioif __name__ == "__main__":#img = data.coffee()img = io.imread('D:\shuzi_image\cat.jpg')img=color.rgb2gray(img)#直接读为灰度图像f = np.fft.fft2(img)fshift = np.fft.fftshift(f)#取绝对值：将复数变化成实数#取对数的目的为了将数据变化到0-255s1 = np.log(np.abs(fshift))"""巴特沃斯低通滤波器"""def butterworthPassFilter(image, d, n):f = np.fft.fft2(image)fshift = np.fft.fftshift(f)def make_transform_matrix(d):transfor_matrix = np.zeros(image.shape)center_point = tuple(map(lambda x: (x - 1) / 2, s1.shape))for i in range(transfor_matrix.shape[0]):for j in range(transfor_matrix.shape[1]):def cal_distance(pa, pb):from math import sqrtdis = sqrt((pa[0] - pb[0]) ** 2 + (pa[1] - pb[1]) ** 2)return disdis = cal_distance(center_point, (i, j))transfor_matrix[i, j] = 1 / (1 + (dis / d) ** (2*n))return transfor_matrixd_matrix = make_transform_matrix(d)new_img = np.abs(np.fft.ifft2(np.fft.ifftshift(fshift * d_matrix)))return new_imgplt.subplot(221)plt.axis("off")plt.title('Original')plt.imshow(img,cmap='gray')plt.subplot(222)plt.axis('off')plt.title('Butter D=100 n=1')butter_100_1=butterworthPassFilter(img,100,1)plt.imshow(butter_100_1,cmap='gray')plt.subplot(223)plt.axis('off')plt.title('Butter D=40 n=1')butter_30_1=butterworthPassFilter(img,40,3)plt.imshow(butter_30_1,cmap='gray')plt.subplot(224)plt.axis('off')plt.title('Butter D=40 n=5')butter_30_5=butterworthPassFilter(img,40,5)plt.imshow(butter_30_5,cmap='gray')
plt.show()

当设置不同的截断频率D,和不同的函数的阶n时，图像的结果如下：
在这里插入图片描述
在这里插入图片描述

图 14 二维图像的巴特沃斯低通滤波结果

  从实验中可以看出，用此滤波后的输出图像振铃现象不明显。n=1时，过渡最平滑，即尾部包含有大量的高频成分，所以一阶低通滤波器没有振铃现象;但随着n的增加，振铃现象会越来越明显，而且当截止频率D设置得越小时，滤波后的图像越模糊。

七、实验总结

  •   （1）傅里叶变换是一种正交数学变换，可以将一维信号或函数分解为具有不同频率、不同幅度的正弦信号或余弦信号的组合。几乎“所有”信号或函数都可以分解成简单的正弦波和余弦波之和。
  •   （2）二维傅里叶变换本质是将一维变换向二维进行拓展。图像经傅里叶变换后，直流分量与图像均值成正比，高频分量则表明了图像中目标边缘的强度及方向。二维离散傅里叶变换，可视为由沿着x、y方向的两个一维傅里叶变换所构成。这一性质可有效降低二维傅里叶变换的计算复杂性，而且得到效果和一般图像的二维傅里叶变换结果一样。
  •   （3）理想低通滤波器的含小于D的频率，即以D为半径的圆内的有频率分量可以完全无损地通过,而圆外的频率,即大于D的频率分量则完全被除掉。理想低通滤波器的平滑作用非常明显，当截断频率D设置得越大时，中心频谱的范围越大，即更多的频率分量可以完全无损的通过，图像越清晰。当D设置得越小时，出现了明显的振铃现象，滤波后的图像越模糊。
  •   （4）与理想低通滤波器相比，高低频之间过渡较为平滑，用此滤波后的输出图像振铃现象不明显。n=1时，过渡最平滑，即尾部包含有大量的高频成分，所以一阶Butterworth低通滤波器没有振铃现象;但随着n的增加，振铃现象会越来越明显。

http://chatgpt.dhexx.cn/article/DPmHPCcl.shtml

相关文章

将两张图片合并成一个PDF，不收费

将两张图片合并成一个PDF，不收费

如何来实现将两张图片合并成一个PDF? 我试过WPS金山、Adobe、万兴等等PDF软件&#xff0c;他们NND都是要收费&#xff01; 咱也不是钱多到大水飘过来的&#xff0c;这里给出最简单的方式&#xff0c;用Windows自带的打印功能&#xff0c;就能实现&#xff01; 最重要的是&…
阅读更多...
pdf转高清图片

pdf转高清图片

很多人在java中遇到ppt/pdf转图片的时候&#xff0c;有些插图图片转不了或者是转出来的图片不清晰&#xff0c;也都是使用的官方jar包。有些是需要引用到icepdf插件的&#xff0c;这里不细说了&#xff0c;直接放一段稍微简单一点的代码供参考&#xff1a; package test;impor…
阅读更多...
锐化pdf文件（图片形式）

锐化pdf文件（图片形式）

目录 前言 正文 1、使用PDF Shaper Pro拆分pdf 2、使用ComicEnhancerPro处理拆分好的图片 3、使用PDF Shaper Pro合并图片为pdf 前言 最近复习考研数学&#xff0c;然后买书真的是死贵死贵&#xff0c;第一次把网上找到的pdf打印出来后发现非常的不清晰&#xff0c;然后开…
阅读更多...
利用C#实现Pdf转图片

利用C#实现Pdf转图片

这周碰到一个需求&#xff0c;由于公司系统框架的原因&#xff0c;不能直接显示第三方回传回来的pdf(说明一下&#xff0c;第三方回传的pdf是带上了签章信息(即在pdf中加入了签名图片))&#xff0c;需要把pdf转成图片进行显示&#xff0c;但在做的过程中踩了不少雷。最后使用第…
阅读更多...
7个值得拥有收藏的免费在线 PDF转图片转换器

7个值得拥有收藏的免费在线 PDF转图片转换器

PDF 格式在文档演示和交换中无处不在。但是PDF转图片的必要性也在于很多情况。这里我想提几点。 收件人可能没有打开您发送的 PDF 的应用程序&#xff0c;但可以使用系统提供的程序查看图像。图像在浏览器中的显示速度比 PDF 快&#xff0c;因为图像可以流式传输&#xff0c;但…
阅读更多...
图片批量合成PDF方法

图片批量合成PDF方法

目录 方法&#xff1a;操作多图合成一个PDF图片文件夹合成PDF批量对每个文件夹中图片合成PDF 如何获取软件 方法&#xff1a; 下载FreePic2Pdf软件&#xff0c;按下面方法操作 操作 多图合成一个PDF 打开FreePic2Pdf.exe软件点击下图1&#xff0c;选择图片添加进来点击下图…
阅读更多...
android中pdf转换成图片格式,Android-PDF转图片

android中pdf转换成图片格式,Android-PDF转图片

场景 将PDF里面的内容渲染到原生的View上面&#xff0c;一直没接触过这部分的技术&#xff0c;所以在网上寻找了下&#xff0c;终于发现了Android原生自带的类&#xff0c;也是今天我们着重讲的内容。 PdfRenderer 从名字上可以看出&#xff0c;这个是和渲染有关系的类型。这里…
阅读更多...
Qt 导出pdf文件(表格、图片)

Qt 导出pdf文件(表格、图片)

1.需要用的类 pro文件添加 QT printsupport QPdfWriter&#xff1a;写pdf的类 QTextDocument&#xff1a;支持html表格、图片的类 2.需要打印的界面 这里示例打印两个表格&#xff0c;一个水平方向的&#xff0c;一个垂直方向的&#xff0c;加一张图片。 3.保存的pdf效果…
阅读更多...
将图片型pdf转成可选中文字型pdf（免费）

将图片型pdf转成可选中文字型pdf（免费）

在使用pdf过程中我们会遇到有些pdf不能进行标注的问题&#xff0c;这是由于有些pdf是扫描版的&#xff0c; 整个pdf是由一张张图片构成的&#xff0c;这样的pdf是不能选中文字&#xff0c;所以也无法进行标注。 本教程教你如何免费将图片型pdf转成可选中文字型pdf。土豪免入~~利…
阅读更多...
怎么把图片变成PDF

怎么把图片变成PDF

在日常办公中&#xff0c;如果我们需要传输图片的话一般是比较简单的&#xff0c;但是如果需要传输很多张图片&#xff0c;不管是发送还是接收的话一张张的处理就比较麻烦了。这种情况下很多朋友或许都会将图片制作成PDF文件。这样技能方便传输也能方便查阅。那么怎么把图片变成…
阅读更多...
PHP 实现PDF转图片

PHP 实现PDF转图片

目录 1.环境配置&#xff1a; 2.实现原理&#xff1a; 3.安装php扩展imagick 4.安装ghostscript 5.pdf转图片 1.环境配置&#xff1a; 2.实现原理&#xff1a; Php使用扩展插件imagick进行图片处理&#xff0c;处理pdf时使用imagick去调用ghostscript 3.安装php扩展imag…
阅读更多...
图片PDF转word

图片PDF转word

最近需要把PDF转word&#xff0c;试了几个网站发现PDF是图片做成的而不是文本直接做的。 找了些国内的软件都要收费。 直接放网站&#xff1a;https://www.onlineocr.net/ 限制&#xff1a;只有50页的免费权限 使用&#xff1a; 1 点右上角SIGN UP 去注册一个账号&#x…
阅读更多...
【PS】免费 使用PS批量将pdf转换成图片 pdf转图片 pdf转jpg pdf转png

【PS】免费 使用PS批量将pdf转换成图片 pdf转图片 pdf转jpg pdf转png

将各种各样的pdf转成图片&#xff0c;是比较普遍的需求&#xff0c;不过目前的各种转换器&#xff0c;不是收费&#xff0c;就是限制转换数量&#xff0c;要不就是强制加水印&#xff0c;很烦。 这里我们使用PS打开PDF&#xff0c;然后使用PS的宏&#xff0c;一键将图片保存到…
阅读更多...
Python提取PDF中的图片

Python提取PDF中的图片

⚡插播一条老家自产的糖心苹果&#xff0c;多个品种&#xff0c;欢迎选购&#xff01;有问题随时私信我⚡&#xff1a; &#x1f34e;&#x1f34e;来自雪域高原的馈赠——海拔2000米的大凉山高原生态糖心苹果&#x1f34e;&#x1f34e;https://blog.csdn.net/qq_15969343/art…
阅读更多...
图片怎么转换成PDF，这三个方法轻松搞定！

图片怎么转换成PDF，这三个方法轻松搞定！

图片转PDF是指将图片文件转换为PDF文件的过程。PDF&#xff08;Portable Document Format&#xff09;是一种文件格式&#xff0c;能够保存文本、图像、表格等多种元素。PDF文件具有跨平台性、可打印性和可搜索性等优点&#xff0c;因此被广泛应用在文档分享、文档存储和文档打…
阅读更多...
图片转为pdf怎么弄？发送图片安全高效的格式

图片转为pdf怎么弄？发送图片安全高效的格式

图片转为pdf怎么弄&#xff1f;pdf文档作为当下最火的一种文档格式之一&#xff0c;我们在日常生活中会经常使用到它。这种格式的文件保密性高&#xff0c;不易被修改。而将图片转换为pdf格式&#xff0c;不仅方便传输图片&#xff0c;而且还能最大程度保证图片的颜色不被改变。…
阅读更多...
如何把图片转换成PDF？4种简单快捷的方法，一键将图片转PDF

如何把图片转换成PDF？4种简单快捷的方法，一键将图片转PDF

分享4种图片转PDF的方法&#xff0c;转换速度快&#xff0c;而且能够保持图片画质清晰&#xff0c;不管是单个图片转换还是多个图片转换&#xff0c;都能满足你&#xff01; 一、单张图片转PDF 1、照片查看器 直接使用Win10中自带的图片查看器&#xff0c;就能将图片转换为P…
阅读更多...
Pycharm远程开发教程

Pycharm远程开发教程

Pycharm远程开发教程 最近项目中使用到了Pycharm的远程开发&#xff0c;记录一下具体的使用方式&#xff0c;本文涉及到的操作均为Pycharm专业版&#xff08;环境为Win10和Ubuntu16&#xff09;&#xff0c;社区版功能没有这么丰富&#xff0c;使用学生邮箱(.edu后缀)注册Jetbr…
阅读更多...
CSS+HTML+JS----开发简单个人网站

CSS+HTML+JS----开发简单个人网站

今天闲着没事花了几个小时写了个个人网站&#xff1b;在盒子布局上花了点时间。 个人网站共六个静态界面&#xff0c;每个界面都有隐藏的音乐&#xff0c;自动播放。 个人网站分为三个部分&#xff0c;登录界面&#xff0c;主界面&#xff0c;以及分界面。 登陆界面主要核心…
阅读更多...
微信机器人开发，个人微信开发

微信机器人开发，个人微信开发

由于自身在机器人方面滚爬多年&#xff0c;现在收藏几个宝藏机器人 推荐一下自己常用的机器人&#xff1a; 不得不吹爆这家伙&#xff0c;适合有技术开发的公司&#xff0c;可以自主开发所需要的功能&#xff01;十分齐全
阅读更多...
推荐文章

Copyright @ 2022~2023