实验目的
通过本次实验学习判别分析在SPSS软件中的具体操作方法,依据变量的各个特征来对变量进行分组,与聚类分析不同的是判别分析对于类别是已知的。
实验步骤及过程:
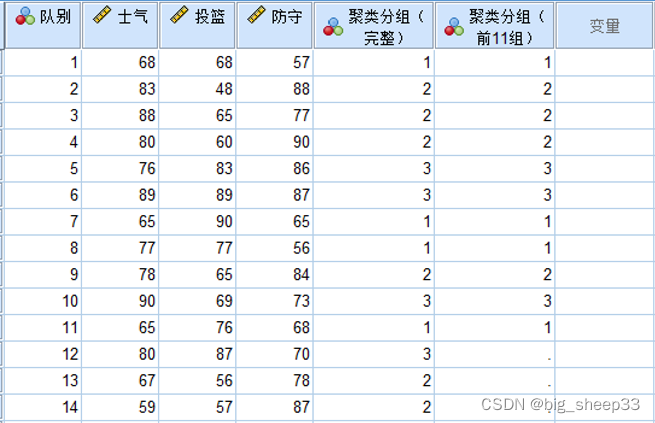
首先对14组数据做聚类分析,通过快速聚类法分为3类作为判别分组变量,然后挑选出后三组数据作为测试集,用来验证判别分析的准确性,聚类之后删除掉后三行数据的分组信息,在此基础上做判别分析。
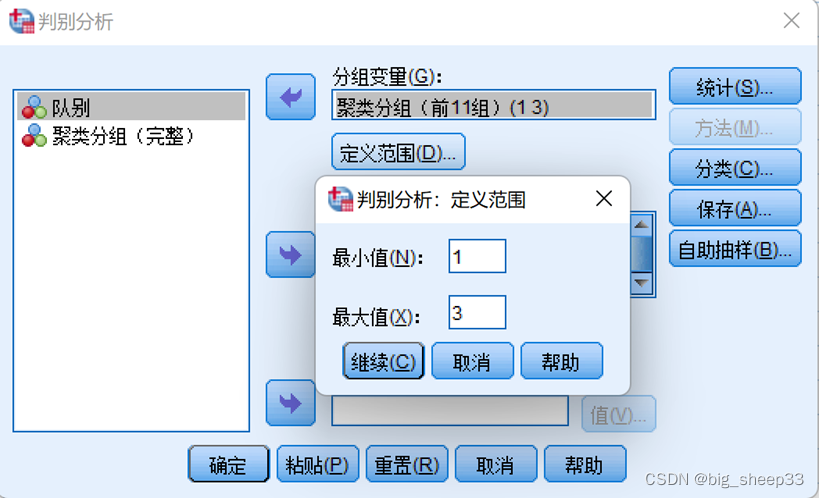
依菜单选择“分析”→“分类”→“判别式”,然后将聚类保存的分组变量加载到“分组变量”框中,定义为类别的范围1到3
接着将要三个自变量加载到“自变量”框,在“统计”选项中勾选需要分析的内容,我们这里勾选相关的选项方便后面的结果分析。
“单变量ANOVA”针对所有自变量进行单因素方差分析,看在各组间有无差别。
“矩阵”框中的选项一般用于模型拟合优度检验,我们这里选择组内相关性。
“函数系数”框中需要注意,“费希尔”方法实际为贝叶斯判法,“未标准化”才是给的费希尔判别法。
在“分类”选项中,一般先验概率都为所有组相等,为自然概率。“显示”中可勾选个案结果,能够输出每个样品判别后的类别、预测分组后验概率及判别得分;“摘要表”输出判别分析正确分组或者错误分组的样品数;
“留一分类”为使用交叉检验法:假设有N个样本,将每一个样本作为测试样本,其它N-1个样本作为训练样本。这样得到N个分类器,N个测试结果,用这N个结果的平均值来衡量模型的性能,相对于手动选择训练集和测试集会方便一些。
最后将预测的组成员、判别得分、组成员概率保存到变量中
实验结果分析与说明
题目一:
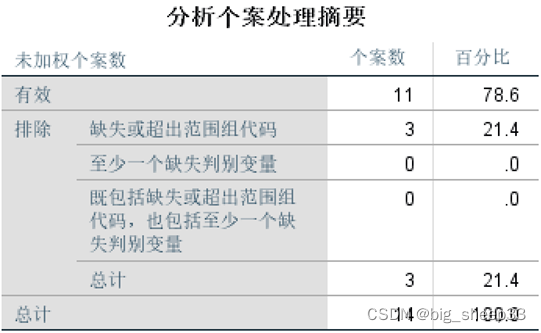
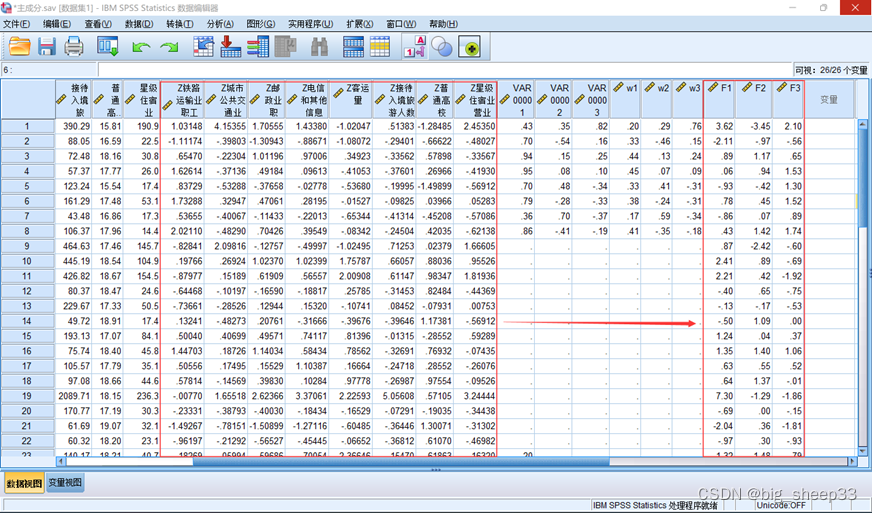
因为我们把后三组分组类别删除作为测试组,所以未分组的有3个数据
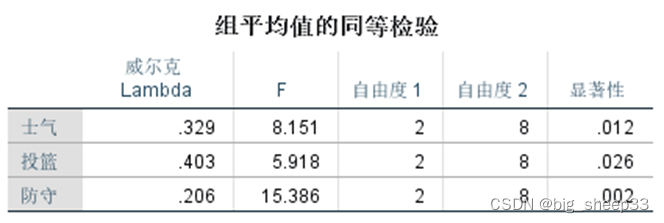
组平均值的同等检验是检验3组变量中的均值是否相等的假设检验,结果显示在0.05的显著性水平下,所有变量的均值互相之间并没有显著性差异。
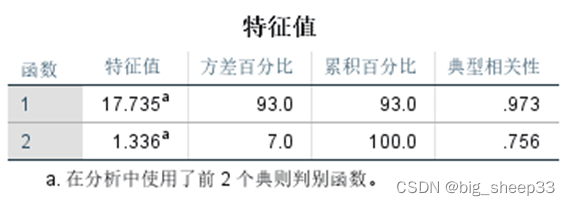
从典则判别函数的输出可以看出,第一判别函数解释了93%的方差,第二判别函数仅仅解释了7%的方差,两个判别函数解释了全部的方差。
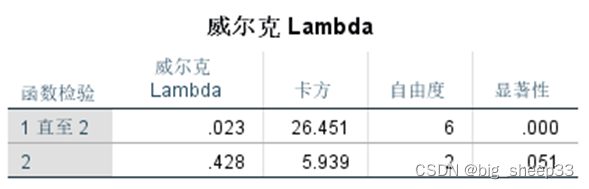
威尔克lambda表对比了两个判别函数的显著性,判别函数一P值为0,在显著性水平α为0.05时显著小于α,而判别函数二P值概率为0.051略大于0,05,不显著,所以后面只对判别函数1展开分析
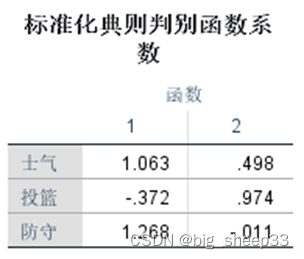
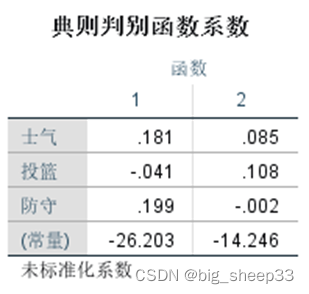
典则判别函数系数表给出了两个判别函数表达式的各项系数,我们可以依据系数写出标准化和未标准化的函数,将要判别的数据带入函数中便能得到判别得分。
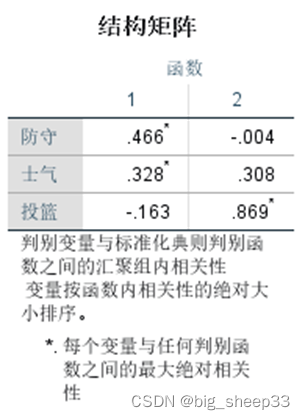
结构矩阵,为判别载荷,标准化系数为判别权重,由判别权重和判别载荷可以知道哪些解释变量对判别函数的影响程度较大。在判别函数1中,防守和士气的贡献较大。
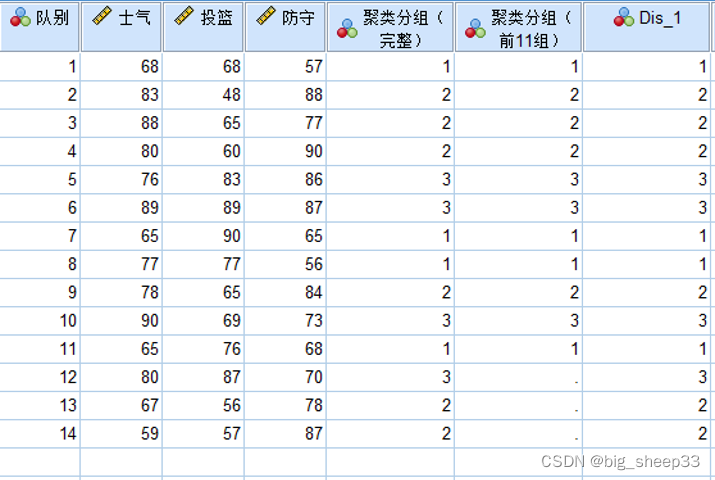
观察保存的分组数据发现,使用判别分析对于后三组的分类与其原始聚类分组结果一致。
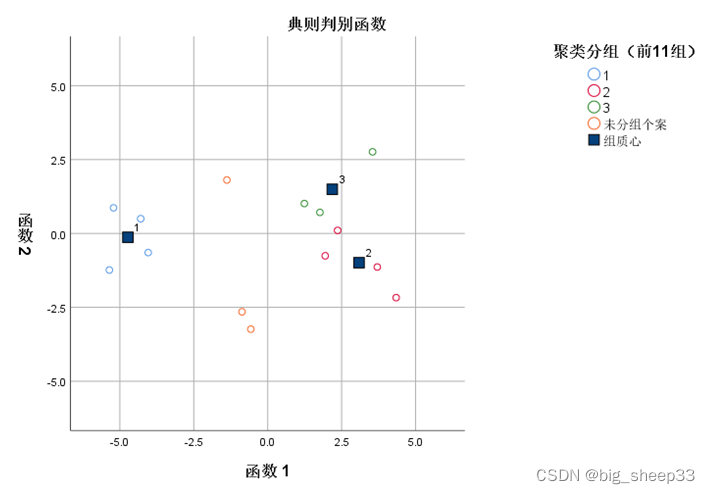
得到的合并图如上所示,可以清楚地看到三类分组,同时包含了未分组的3个点。
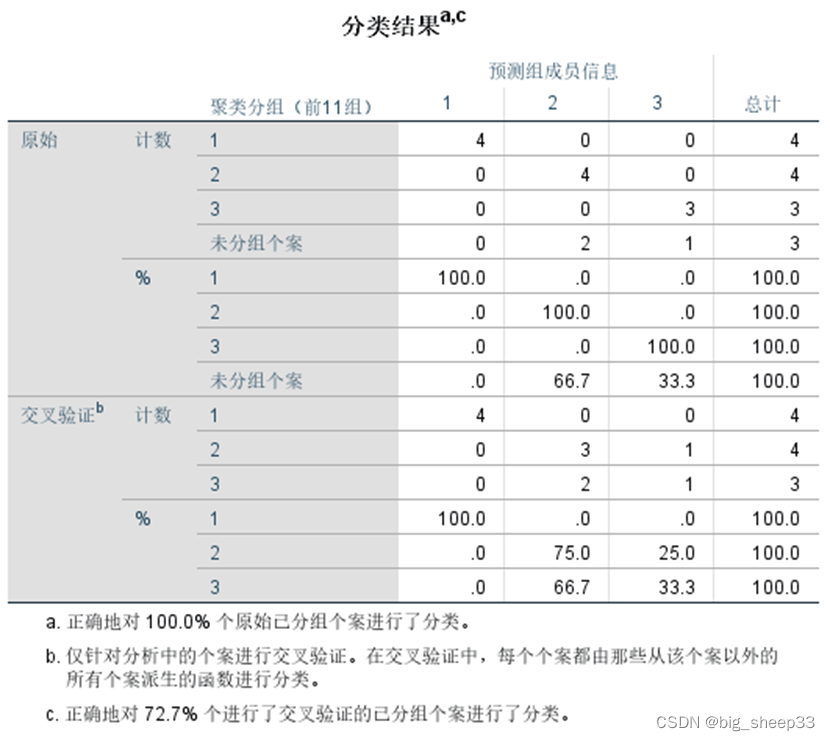
交叉检验结果可知,本次判别分析分类正确率为72.7%,第三组有一个数据被错误分到了第二类,第二组有两个数据被错误分到了第三类。