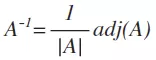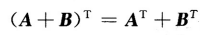关于分块矩阵求逆，其中对角矩阵比较简单，我看很多人都写了，并且很详细。
但关于AUVD的分块矩阵我没看到太让我明白的，可能我get不到点，数学基础差，我就自己写了详细的步骤。
我写的这个条件是A可逆，如果A，D都可逆更简单，但我没有写，如果看完这个想了解A，D均可逆的可以给我留言，我再写一篇。
整体思路就是按照定义求解：
1，设逆矩阵；
2.根据AA-＝I列出四个等式（I就是单位矩阵E）；
3.四个等式，四个未知，所以根据其中两个等式可以用其中一个未知表示出另一个未知。
我觉得需要注意的是，当条件是A可逆和A与D均可逆时，利用的等式不太一样。
例如这里是A可逆，所以利用式子①和②，然后代入③和④；
如果条件是A和D都可逆，那么应该利用式子②和③，然后代入①和④
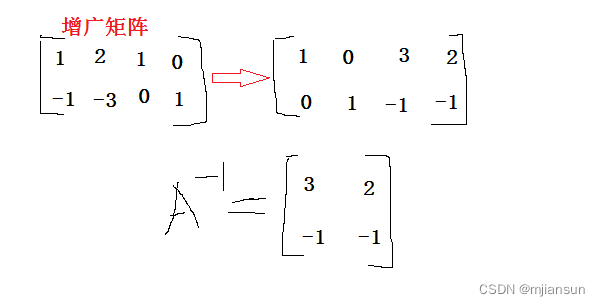
所以最后答案是
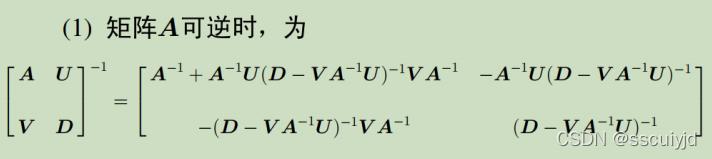
有问题可以留言。
