矩阵的逆
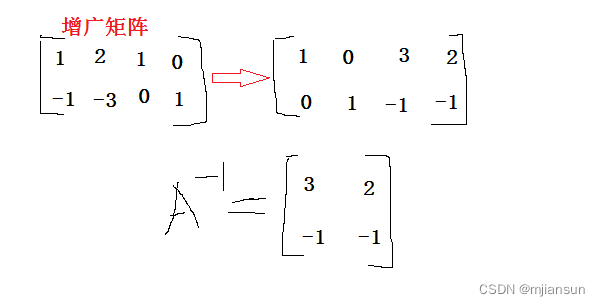
原理:
连接:
https://baike.baidu.com/item/%E9%80%86%E7%9F%A9%E9%98%B5




代码:
QT c++版:
//求逆矩阵
QVector<QVector<double>> Matrix_inverse(QVector<QVector<double>> &A)
{int cols = A[0].size();int rows = A.size();QVector<double> col(cols,0);QVector<QVector<double>> res(rows,col);int i,j,k;double temp,temp2;//初始单位阵for (i = 0; i < rows; i++){for (j = 0; j < rows; j++){res[i][j] = (i == j) ? 1 : 0;}}// 求左下for (i = 0; i <= rows - 1; i++){//提取该行的主对角线元素temp2 = A[i][i]; //可能为0if (temp2 == 0) //为0 时,在下方搜索一行不为0的行并交换{for (i = 0; i < rows; i++){k = i;for (j = i + 1; j < rows; j++){if (A[j][i] != 0) //不为0的元素{k = j;break;}}if (k != i) //如果没有发生交换: 情况1 下方元素也全是0{for (j = 0; j < rows; j++){//行交换temp = A[i][j];A[i][j] = A[k][j];A[k][j] = temp;//伴随交换temp = res[i][j];res[i][j] = res[k][j];res[k][j] = temp;}}else {//满足条件1cout<<"不可逆矩阵ERROR"<<endl;break;}}}//该行除以主对角线元素的值 使主对角线元素为1for(j = 0; j<rows; j++){A[i][j] = A[i][j] / temp2; //分母不为0res[i][j] = res[i][j] / temp2; //伴随矩阵}//下方的每一行减去该行的倍数for(k = i+1; k<rows; k++){temp2 = A[k][i]; //下方的某一行的主对角线元素for (j = 0; j < rows ; j++){A[k][j] = A[k][j] - temp2 * A[i][j]; //下方的每一行减去该行的倍数 使左下角矩阵化为0res[k][j] = res[k][j] - temp2 * res[i][j]; //左下伴随矩阵}}}temp2 = A[rows - 1][rows - 1]; //最后一行最后一个元素if (temp2 == 0) //条件2 初步计算后最后一行全是0 在只上步骤中没有计算最后一行,所以可能会遗漏{cout<<"不可逆矩阵,ERROR"<<endl;}A[rows - 1][rows - 1] = 1;for (j = 0; j < rows; j++){res[rows - 1][j] = res[rows - 1][j] / temp2;}// 求右上for (i = rows - 1; i >= 0; i--){for (k = i - 1; k >= 0; k--){temp2 = A[k][i];for (j = 0; j < rows; j++){A[k][j] = A[k][j] - temp2 * A[i][j];res[k][j] = res[k][j] - temp2 * res[i][j];}}}return res;
}vs c++版:
#include <cmath>#include <iostream>using namespace std;double ffabs(double p) //计算实数的绝对值{double q;q = fabs(p);return(q);}double ff(double p) //计算1.0/p{double q;q = 1.0/p;return(q);}//a 原矩阵。返回逆矩阵。
//n 矩阵阶数template <class T> //模板声明T为类型参数int inv(T a[], int n) //若矩阵奇异,则返回标志值0,否则返回标志值非0。{ int *is,*js,i,j,k,l,u,v;double d, q;T p;is=new int[n];js=new int[n];for (k=0; k<=n-1; k++){ d=0.0;for (i=k; i<=n-1; i++) //选主元for (j=k; j<=n-1; j++){ l=i*n+j; q = ffabs(a[l]); //计算元素绝对值(模)if (q>d) { d=q; is[k]=i; js[k]=j;}}if (d+1.0==1.0) //矩阵奇异{ delete[] is; delete[] js; cout <<"矩阵奇异!" <<endl;return(0); //返回奇异标志值}if (is[k]!=k)for (j=0; j<=n-1; j++) //行交换{ u=k*n+j; v=is[k]*n+j;p=a[u]; a[u]=a[v]; a[v]=p;}if (js[k]!=k)for (i=0; i<=n-1; i++) //列交换{ u=i*n+k; v=i*n+js[k];p=a[u]; a[u]=a[v]; a[v]=p;}l=k*n+k;a[l] = ff(a[l]); //计算1/a[l]for (j=0; j<=n-1; j++) //归一化if (j!=k){ u=k*n+j; a[u]=a[u]*a[l];}for (i=0; i<=n-1; i++) //消元计算if (i!=k)for (j=0; j<=n-1; j++)if (j!=k){ u=i*n+j;a[u]=a[u]-a[i*n+k]*a[k*n+j];}for (i=0; i<=n-1; i++)if (i!=k){ u=i*n+k; a[u]=(a[u]-a[u]-a[u])*a[l];}}for (k=n-1; k>=0; k--) //恢复行列交换{ if (js[k]!=k)for (j=0; j<=n-1; j++){ u=k*n+j; v=js[k]*n+j;p=a[u]; a[u]=a[v]; a[v]=p;}if (is[k]!=k)for (i=0; i<=n-1; i++){u=i*n+k; v=i*n+is[k];p=a[u]; a[u]=a[v]; a[v]=p;}}delete[] is; delete[] js;return(1);}test 测试:
#include <cmath>
#include <iostream>using namespace std;int main(){ int i,j;double a[4][4]={ {0.2368,0.2471,0.2568,1.2671},{1.1161,0.1254,0.1397,0.1490},{0.1582,1.1675,0.1768,0.1871},{0.1968,0.2071,1.2168,0.2271}};double b[4][4];for (i=0; i<=3; i++)for (j=0; j<=3; j++) b[i][j]=a[i][j];i=inv(&b[0][0],4);if (i!=0){ cout <<"实矩阵 A:" <<endl;for (i=0; i<=3; i++){ for (j=0; j<=3; j++) cout <<a[i][j]<<" ";cout <<endl;}cout <<"逆矩阵 A-:" <<endl;;for (i=0; i<=3; i++){ for (j=0; j<=3; j++) cout <<b[i][j]<<" ";cout <<endl;}}return 0;}