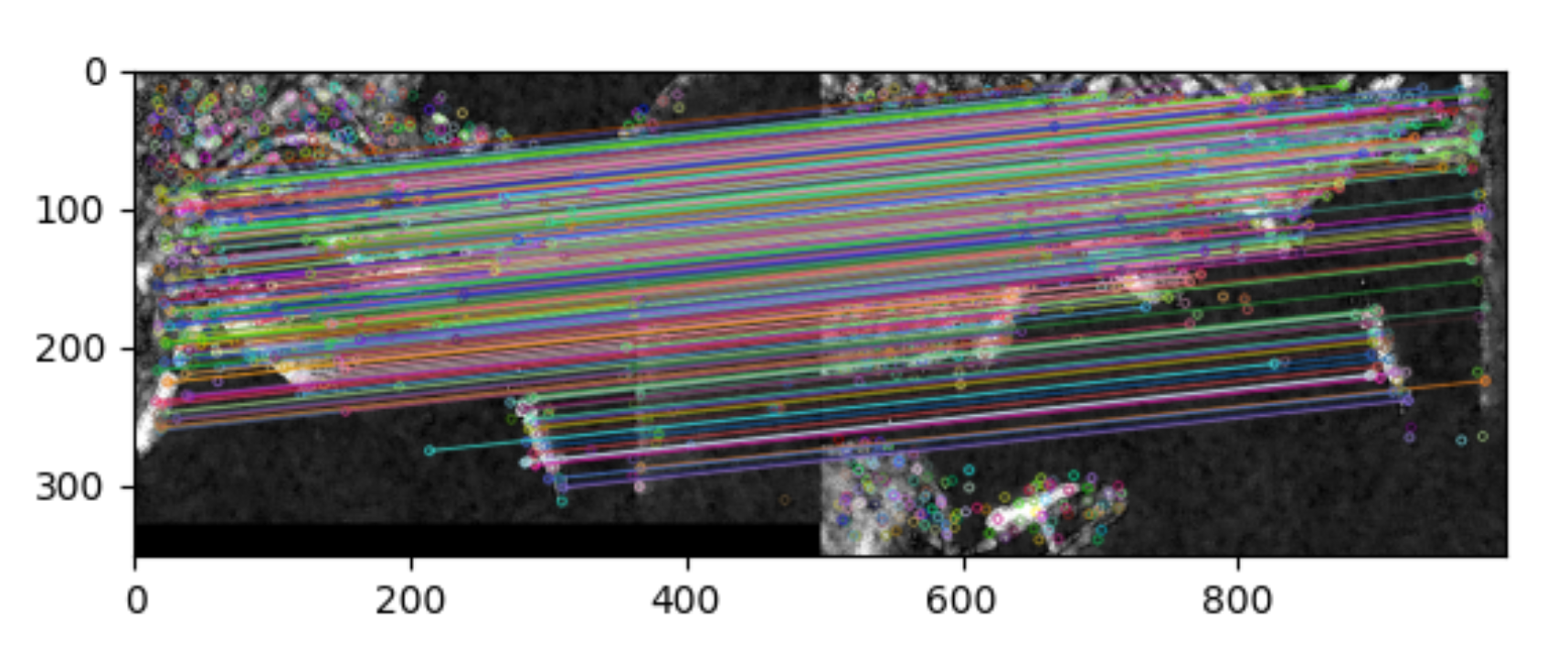
简介：SIFT算法是检测和描述局部特征的一种方法，具有尺度不变性，对于光线，噪声等的容忍度相当高。即便少数几个物体也可以产生大量SIFT特征。

SIFT算法实质上是在不同尺度空间上查找关键点，并计算出关键点的方向。

算法步骤：

1.构建尺度空间

•  利用高斯核来构建
  • 高斯核是唯一可以产生多尺度空间的核，也是唯一线性核，利用高斯核对图像模糊处理不会引入其他噪声。
  • 高斯核函数：

• 输入图像通过高斯核函数连续的对尺度进行参数变换，最终得到多尺度空间序列。图像中某一尺度的空间函数由高斯函数和原输入图像I(x,y)卷积得出：

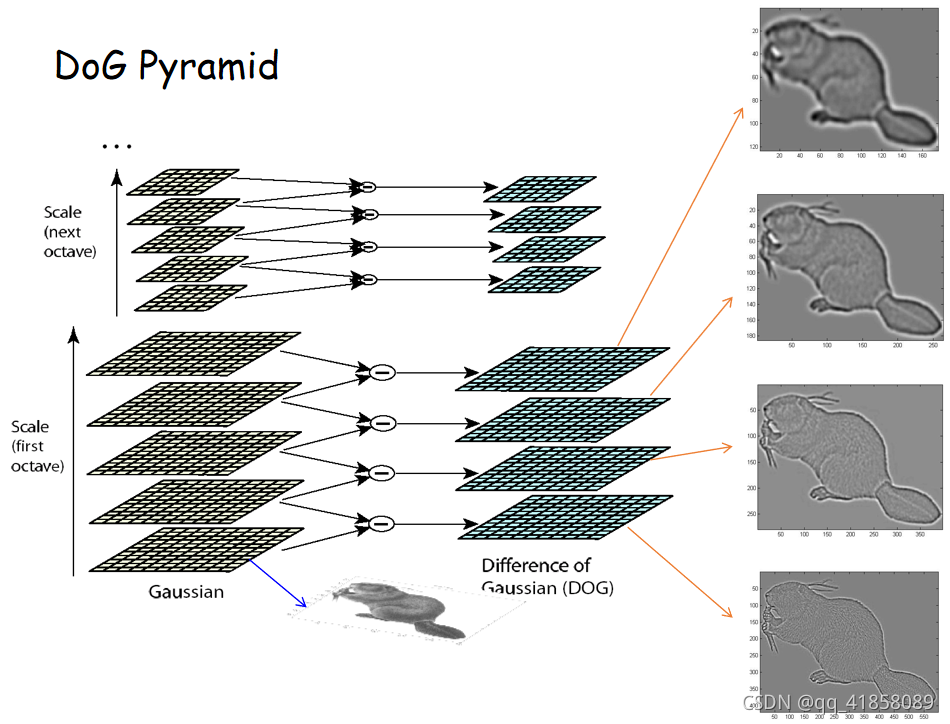
• 高斯金字塔
  • 模仿图像的不同尺度
  • 生成步骤：高斯平滑-->对图像做下采样（一般先将图像扩大一倍，在扩大的图像基础上构建高斯金字塔，然后您对该尺寸下图像进行高斯模糊，几幅模糊的图像集合构成了一个八度，然后对该八度下倒数第三张图片进行下采样，长和宽分别缩短一倍，图像面积变为原来的四分之一。以此类推）
  • 为什么选倒数第三张进行下采样？为了保持尺度空间的连续性，根据下图公式可以计算得出第o组第S层的图像尺度，可以发现下一组的第o层图像恰好和上一组倒数第三张图一致，所以每一组的第0张图像只需要用上一层的倒数第三张进行下采样即可。

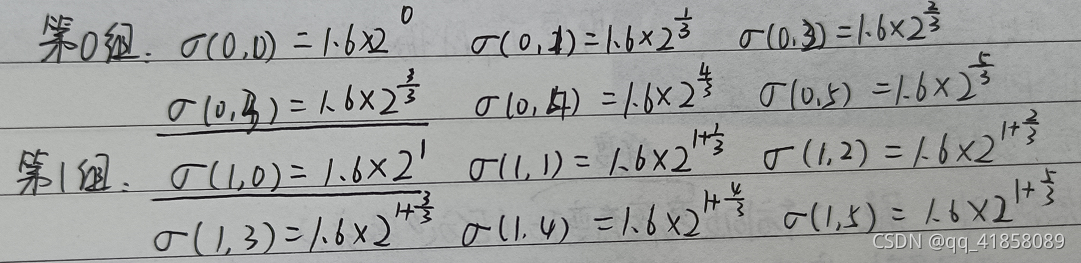
2.DoG

• Laplace operator:二阶导

• LoG(Laplace of Gaussian)
  • 把拉普拉斯算子和高斯函数联合到了一个步骤
  • 等价于先对高斯函数求二阶导，再与原图进行卷积

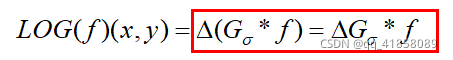
将高斯拉普拉斯算子展开：

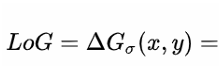
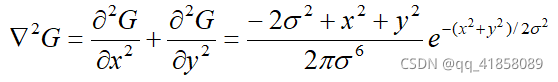
又有：

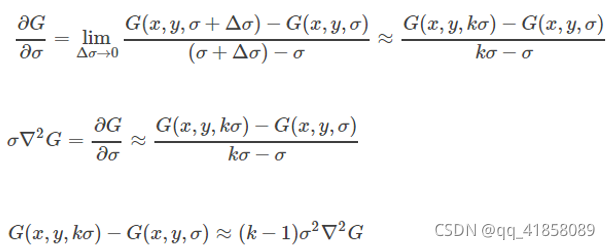
• DoG：对不同尺度下的高斯函数的差分

DoG算子为

DoG算子和LoG算子具有类似的波形，且计算复杂度低，所以一般用DoG代替LoG算子。

• DoG vs LoG

• 高斯差分图像

3.DoG定位极值点

• 特征点是由DoG空间的局部极值点组成的。
• 每一个像素要和他所有的相邻点比较（中间的监测点和它同尺度的8个相邻点和上下相邻尺度对应的9*2个，共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点）

1. 确定潜在特征点

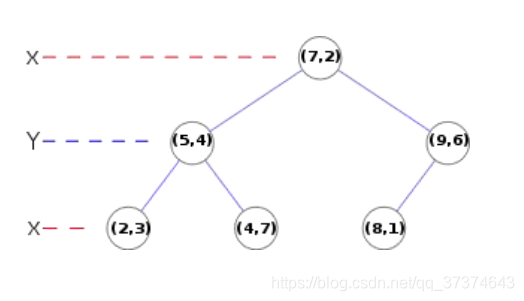
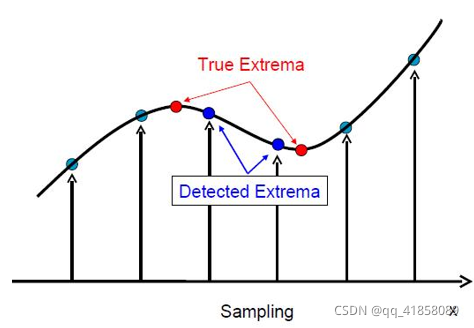
• 检测到的局部极值点A（x,y,σ）是离散情况下的一个极值点，如果考虑连续情况，则极值点可能落在了A点的附近(Δx,Δy,Δσ)（如下图所示），而真正的极值点B可以表示为在点A处的泰勒展开。

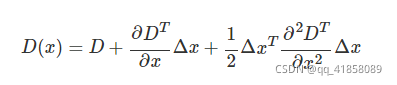
令上面D(x)的一阶导数为0，可以得到

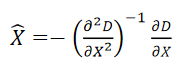
• 对以上过程进行多次迭代（最多5次）得到最终候选点的精确位置.(偏移超过0.5时更新当前像素点，若没有超过0.5，则当前像素加上偏移就是精确点)

4.边缘和低对比度响应（移除某些特征点）

• 移除低对比度的点：D(X')小于0.03的点
• 移除边缘点：利用hessian矩阵

5.确定关键点方向

• 利用特征点领域像素的梯度来确定其方向参数
  • 对于已经检测到的特征点，已知其尺度σ,可以确定该尺度下的高斯图像

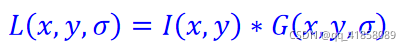
• 梯度方向

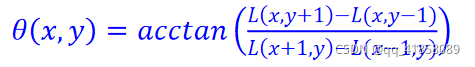
• 梯度幅值

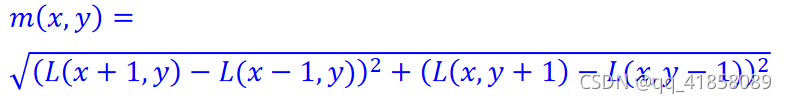
• 利用图像的梯度直方图求取关键点局部结构的稳定方向
  • 以关键点为原点，一定区域内的图像像素点对关键点方向生成所做的贡献。
  • 构建梯度直方图，梯度方向决定位于直方图的哪个槽（共36个槽，每10度划分一个），幅值加权更新槽内幅值的和。

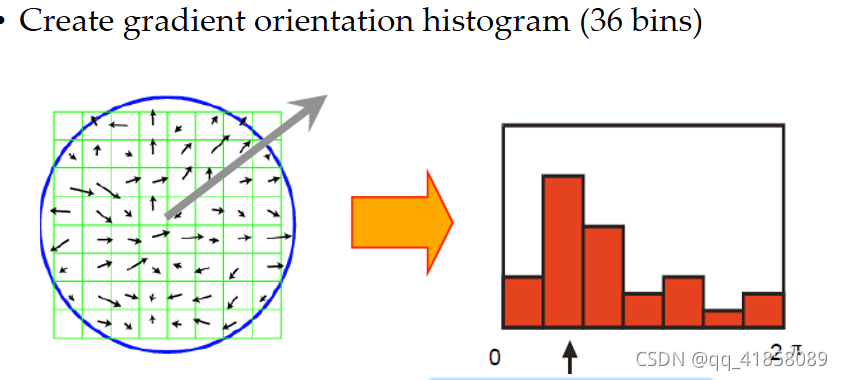
6.构建关键点描述子（keypoints descriptor）

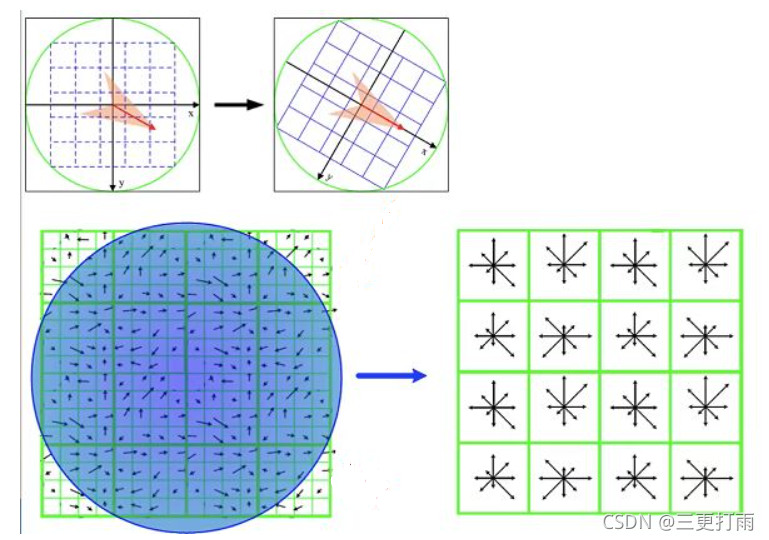
• 校正主方向，确保旋转不变性
  • 以特征点为中心，将坐标轴旋转到特征点的主方向
• 生成描述子，形成128维的特征向量
  • 基于梯度方向直方图，每45度一个划分，共划分8个槽
  • 在每个4*4的小方块内绘制8个方向的梯度直方图，计算幅值，即形成一个种子点
  • 对每个关键点使用16个种子点来描述，每个种子点有8个方向的信息，即形成了128为特征向量

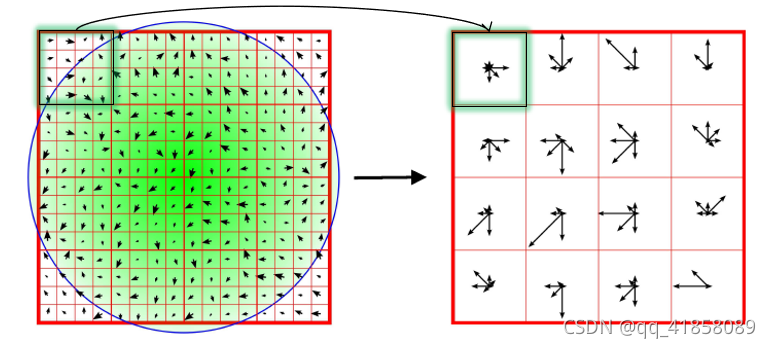
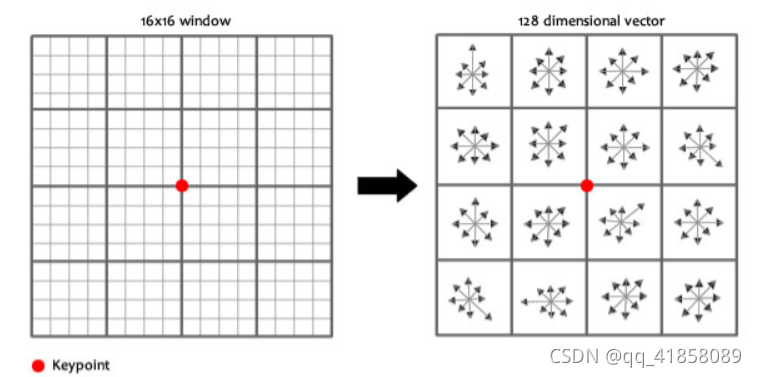
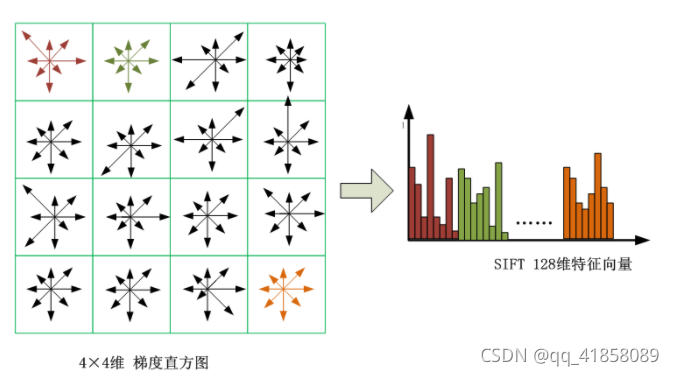
• 归一化处理特征向量的长度，进一步去除光照的影响。

参考博文：

SIFT特征详解 - Brook_icv - 博客园

SIFT解析（二）特征点位置确定 - DreamFaquir - 博客园

SIFT解析（三）生成特征描述子_honpey爱编程-CSDN博客

SIFT定位算法关键步骤的说明 - ☆Ronny丶 - 博客园