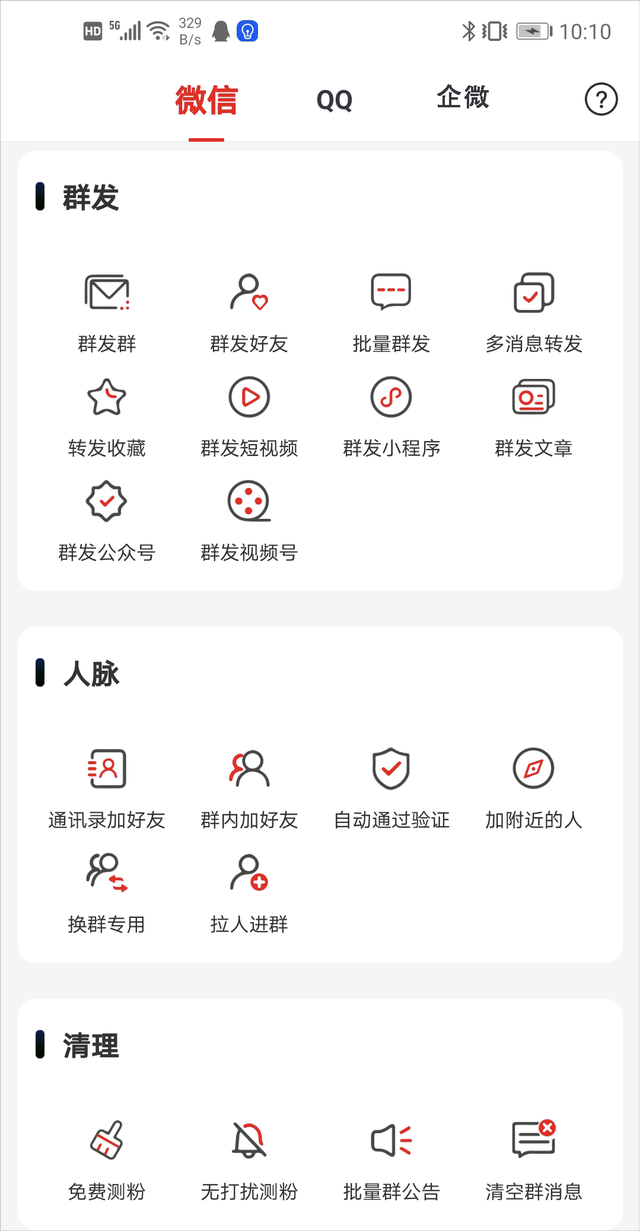
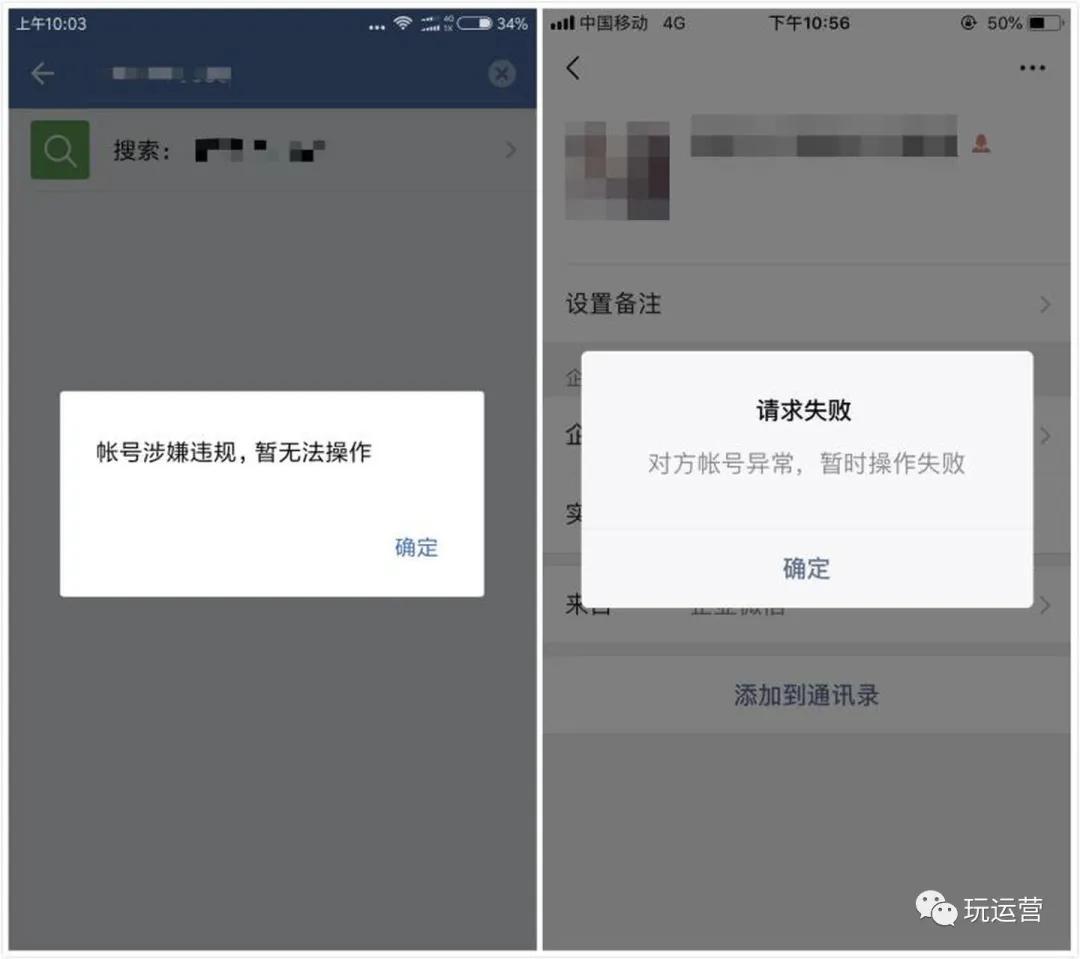
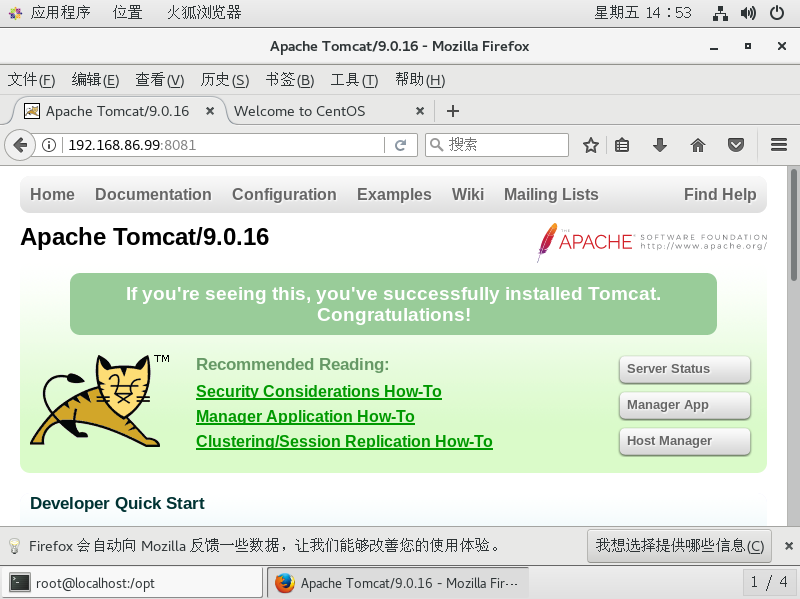
① C'=0(C为常数函数) ② (x^n)'= nx^(n-1) (n∈R);熟记1/X的导数 ③ (sinx)' = cosx (cosx)' = - sinx (tanx)'=1/(cosx)^2=(secx)^2=1+(tanx)^2 (cotx)'=-1/(sinx)^2=-(cscx)^2=-1-(cotx)^2 (secx)'=tanx·secx (cscx)'=-cotx·cscx (arcsinx)'=1/(1-x^2)^1/2 (arccosx)'=-1/(1-x^2)^1/2 (arctanx)'=1/(1+x^2) (arccotx)'=-1/(1+x^2) (arcsecx)'=1/(|x|(x^2-1)^1/2) (arccscx)'=-1/(|x|(x^2-1)^1/2) ④(sinhx)'=coshx (coshx)'=sinhx (tanhx)'=1/(coshx)^2=(sechx)^2 (coth)'=-1/(sinhx)^2=-(cschx)^2 (sechx)'=-tanhx·sechx (cschx)'=-cothx·cschx (arsinhx)'=1/(x^2+1)^1/2 (arcoshx)'=1/(x^2-1)^1/2 (artanhx)'=1/(x^2-1) (|x|<1) (arcothx)'=1/(x^2-1) (|x|>1) (arsechx)'=1/(x(1-x^2)^1/2) (arcschx)'=1/(x(1+x^2)^1/2) ⑤ (e^x)' = e^x (a^x)' = (a^x)lna (ln为自然对数) (Inx)' = 1/x(ln为自然对数) (logax)' =x^(-1) /lna(a>0且a不等于1) (x^1/2)'=[2(x^1/2)]^(-1)(1/x)'=-x^(-2)
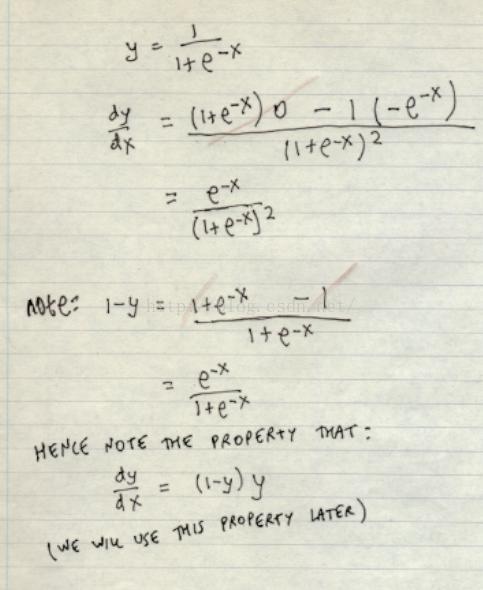
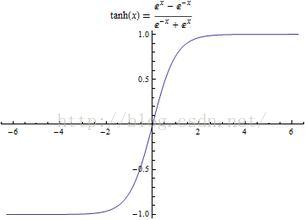
常用函数的导数表
article/2025/9/14 11:39:15
相关文章
【惊呼】微信最多可以加多少好友,真正原因可能出乎你的想象!
为什么微信联系人个数限制为5040而非5000人,这个还真有一定的原因,据说这是根据《理想国》的一本书中描述的理想城邦人数而定,
这本书的作者为古希腊哲学家柏拉图,他所描述的理想城邦人数为5040人,微信之父张小龙认为…
Java并发编程视频分享-第一期
一、主讲人:加多(阿里集团-淘宝技术部-高级开发工程师)
**本名:**翟陆续
目前在阿里巴巴淘宝移动中间件消息服务组工作,热衷并发编程,开源框架,架构设计。
著作:《Java并发编程之美》 二、本次课程内容: 什么是线程?并发与并行区别?为何并发编程那么难?1.数据竞争…
element ui 下拉菜单加多选框
最近做一个项目,需要一个带有多选框功能的下拉菜单,还是老规矩,自己封装一个吧。很简单 写完以后打开页面测试,发现已经选中了,但是输入框并没有显示选择的值 打开vue开发工具,发现选中的值并没有放入value…
一个springboot+mybatisplus+vue实现的增删改查加多条件查询加分页
0.一个小Demo 就没有用到其它的技术了
格式如下 表文件
create table FinancingProduct
(id varchar(50) not nullprimary key,risk int not null,income varchar(50) not null,saleStarting datetime not null,saleEnd datetime …
加多宝首度披露"换头手术"的详细内幕
12 月下旬,加多宝与王老吉的“改名案”和“怕上火案”判决结果先后出台,两大凉茶巨头之间的官司纠纷再起波澜。而加多宝集团品牌管理部负责人王月贵,在出席活动时首度披露了加多宝“换头手术”的详细内幕——由此,加多宝打赢凉茶之…
ASEMI整流桥MB10S出来的电压是多少,MB10S加多大电容
编辑-Z
MB10S参数描述
型号:MB10S
封装:MBS-4 (SOP-4)
特性:小方桥、贴片桥堆
电性参数:1A 1000V
芯片材质:GPP
正向电流(Io):1A
芯片个数:4
正向电压(VF):1.0V
芯片尺寸&…
加多宝李二强:营销数字化闭环初体验,真的很爽
作者 | 中国软件网 曹开彬 艾佳 校对 | 中国软件网 马志学 企业数字化轰轰烈烈二十年,却始终在实践探索的峭壁上攀援。一方面作为技术手段的数字信息科技快速演进,将企业数字化导入泛摩尔定律循环,如逆水行舟不进则退;另一方面数字…
用JavaScript实现,用户输入自己的汽油编号,然后输入自己加多少升,就弹出价格
Ⅰ、问题描述:
一个加油站为了鼓励车主多加油,出行优惠政策: 加的多有优惠: 92 号汽油,每升 6 元;如果大于等于 20 升,那么每升 5.9 元; 97 号汽油,每升 7 元࿱…
微信每天加多少人不会封号?(行业经验)
微信8.0版本开始微信好友的最大数量,将之前的最多5000好友提升到现在的10000好友。
不要相信那些一天加500人1000人的,不可能的!腾讯对这方面是有严格限制的。
但是会区分你的微信号质量,质量越好加人越有利。以下内容是增对普通…
企业微信一天最多可以加多少人? 企业微信加好友功能会被限制吗?
企业微信已经成为私域运营必备工具,最近经常有人问我企业微信一天可以主动加多少人这个问
企业微信已经成为私域运营必备工具,最近经常有人问我企业微信一天可以主动加多少人这个问题,我每次都是很纠结,如果微信告诉你一天可以加多少人,那么大家不就在这个红线下面疯狂的…
❤️创意网页:高考加油倒计时网页文字加多版 - 增加祝福语句和下雪背景效果
✨博主:命运之光 🌸专栏:Python星辰秘典 🐳专栏:web开发(简单好用又好看) ❤️专栏:Java经典程序设计 ☀️博主的其他文章:点击进入博主的主页 前言:欢迎踏入…
tomcat优化(生产环境) 加多实例部署
来做一个tomcat多实例部署
1.首先安装jdk和tomcat 然后复制/usr/local的tomcat
2.配置tomcat环境变量 把两个tomcat都配置一下 环境变量的位置指向不能错
vim /etc/profile.d/tomcat.sh
export CATALINA_HOME1/usr/local/tomcat/ export CATALINA_BASE1/usr/local/tomcat/…
el-table自定义表头,el-table 加多选列
element el-table 加多选列 <el-table :data"tableData" height"500" style"width: 100%" center highlight-current-row ><el-table-column type"index" label"序号" width"50" align"center"…
element-ui下拉选项加多选框(带全部)
代码全在一个页面实现 效果: 代码:
<template><div class"select-checked"><el-select:value"selected"multipleplaceholder"请选择":popper-append-to-body"false"><el-option :value&q…
elementUI之下拉选项加多选框功能实现
elementUI之下拉选项加多选框功能实现 elementUI之下拉加多选框功能实现下拉加多选框升级—添加全部选项需求改版完善 elementUI之下拉加多选框功能实现
因产品需求和UI样式调整,和element自带的下拉多选有冲突,索性自己尝试修改如下:
下拉…
elementUI下拉选项加多选框功能实现(自己添加“全部”选项)
本文包含三部分: 1.下拉加多选框 2.升级—添加全部选项 3.需求改版完善 一、下拉加多选框
效果如下图: 封装如下:
<template><div class"select-checked"><!-- 下拉加多选框 --><el-selectv-model"val…
Js计算指定日期加上多少天,加多少月,加多少年的日期 (实用)
原文出处:Js计算指定日期加上多少天,加多少月,加多少年的日期 - 庞国明 - 博客园Js计算指定日期加上多少天,加多少月,加多少年的日期https://www.cnblogs.com/pangguoming/p/8854999.html
function DateAdd(interva…
加多宝二次创业五周年:解锁品牌持续增长密码
今年作为后疫情时代元年,首要的任务是提振经济、重振信心,其中消费市场的提振至关重要。
春江水暖鸭先知。每当消费市场开始复苏,食品饮料行业的回暖一般会更明显。而要扩大食品饮料的消费规模、提振消费信心,关键在于品牌结合外…
阿里技术专家加多:Java异步编程实战之基于JDK中的Future实现异步编程
正文共:14244 字 8 图 预计阅读时间: 36 分钟 本节内容摘自《Java异步编程实战》中的一小节。 一、前言 本节主要讲解如何使用JDK中的Future实现异步编程,这包含如何使用FutureTask实现异步编程以及其内部实现原理以及FutureTask的局限性。 二…
如何理解向量组的秩和矩阵的秩
1
向量组的轶指的是极大线性无关组中向量的个数 矩阵的轶是把一个矩阵分为行向量组和列向量组,这两个向量组的轶分别称为行轶和列轶.可以证明的是行轶和列轶相等,这就是矩阵的轶.
这里提醒一下就是: n-r为线性无关的解向量的个数,而r为极大无关组的个数 n-r也为基础解析向量的…