码制

1.数字系统

用数字信号完成对数字量进行算术运算和逻辑运算的电路称为数字电路，或数字系统。由于它具有逻辑运算和逻辑处理功能，所以又称数字逻辑电路。人类已经进入到了数字时代，数字系统在我们日常生活中愈发重要，并广泛应用于通信、商贸、交通控制、航空航天、医疗、天气检测、互联网等等重要领域。人们从而拥有了数字电话、数字电视、数字通用光盘、数字相机等等数字化设备。数字系统的一个特性是其通用性，它可以执行一系列的指令，对给定程序进行操作和处理；它的另一特性是具备描述和处理离散信息的能力，我们知道，任何一个取值数目有限的元素集都包含着离散信息，如十进制的各个数、字母表的26个字母等等。数字系统中的离散信息可由“信号”进行表示，最常见的信号就是电压和电流，它们一般由晶体管构成的电路产生。目前，在各种数字电子系统中的电信号只有两种离散值，因而也被称为二进制。

数字设计方法发展的主要趋势是采用硬件描述语言(HDL)描述和模拟数字电路的功能，HDL类似于编程语言，非常适合于以文本的形式描述数字电路。利用HDL可以在硬件电路建立之前模拟和验证数字系统的功能。HDL也可以和逻辑工具一起，用于数字系统的自动设计过程。因此，熟悉一种硬件描述语言并掌握基于硬件描述语言的设计方法是十分重要的。

综上所述，数字系统处理二进制形式表示的离散信息值。用于计算的操作数可以表示成二进制数的形式。其它离散元素，包括十进制数和字母表中字母也可以利用二进制码来表示。在下一小节，我们会着重向大家介绍二进制码。

2.二进制数

在数学和数字电路中，二进制(binary)数是指用二进制记数系统，即以2为基数的记数系统表示的数字。这一系统中，数通常用两个不同的符号0(代表零)和1(代表一)来表示。以2为基数代表系统是二进位制的。数字电子电路中，逻辑门的实现直接应用了二进制，因此现代的计算机和依赖计算机的设备里都用到二进制。每个数字称为一个比特(二进制位)。

那么，二进制与其它进制是什么关系呢？

其实很简单，举个例子，十进制数234，234等于2个百加上3个十加上4个一，可以写为：

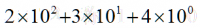
然而，按照惯例，幂次从左到右递增，带小数点的十进制数即可表示为(此处例子为10位数)：

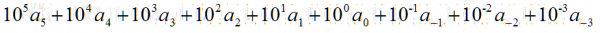
如果，十进制的数为234，那么a2=2,a1=3,a0=4；

读到这里，相信您也能领会10进制的系数与位数的对应关系与计算方法，那么二进制如何计算呢？

由于十进制只能使用是个数字，每个系数均要与10的幂次相乘，因此，十进制的基数为10。二进制与十进制是不同的数制，其系数只有两种取值“0”和“1”，所以，每个系数都要乘以基数的幂，结果相加后就是10进制数，举个例子，二进制数11010.11相对应的十进制数如何计算呢？

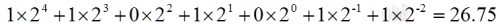
如果这里明白了，我们继续向下推倒，假设我们推广到以r为基数的任何进制呢？我们可推倒出如下公式：

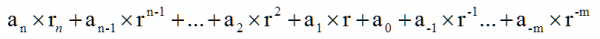
这个公式看起来复杂，但实际使用起来十分简单：举个例子，8进制数127.4,我们把它转化为10进制：

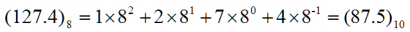
当基数小于10时，我们到对应位数进位即可，例如8进制，我们逢8进位，10进制就是逢10进位，那么16进制我们如何进行处理呢？请参照下表：