查看专栏更多内容:
① 数据库介绍 及 关系型数据库的关系代数表达式
② 关系数据库标准语言SQL 数据定义(创建、修改基本表)、数据更新(增删改)
③ 关系数据库标准语言SQL 数据查询(SELECT)
相关实战:
uni-app 发送网络请求
数据库基础
- 数据库介绍
- 数据模型
- 概念模型
- 逻辑模型
- 关系型数据库
- 关系数据结构
- 基本关系(基本表或基表)的性质
- 关系的完整性
- 基本的关系操作
- 传统的集合运算
- 专门的关系运算
- ① 选择
- ② 投影
- ③ 连接
- 外连接
- ④ 除
写下博客用于自我复习、自我总结。
如有错误之处,请各位指出。
本数据库系列专栏,文章的重心将会是总结SQL语句的使用,而不会涉及到太多数据库本身或大数据的内容。除此以外,使用的SQL语句会因为MySQL或Oracle的不同,导致一些使用上的差异,这部分具体的区别将不作区分。在之后的文章中将会使用MySQL数据库。对于MySQL和Oracle的区别,百度一下此类文章很多。

对于下载MySQL数据库,可以参考我之前的文章:uni-app 发送网络请求。该文章里提到了,如何使用phpstudy去下载MySQL和SQL_Front,并且写了简单创建接口去连接数据库的例子,感兴趣的可以了解一下。而为了能够满足自己写些小项目的需求,总结基本的SQL语句就提上了日程,因为不可能所有逻辑都是简单的增删改查。
数据库介绍
在网络发展如此迅速的今天,信息资源无处不在,而如何有效管理、组织、存储这些数据,将会直接影响各企业或组织的效益。现在要说的数据库(Database)就是处理这些问题的工具。
不过在具体说到数据库之前,我们先了解一下数据模型。
数据模型
数据模型是数据库系统的核心和基础,因为我们要做的就是把现实世界数据的特征抽象出来,而在开发实施数据库应用系统中就涉及到了几个不同的数据模型:概念模型、逻辑模型和物理模型。
这几个模型都是必不可少的,简单叙述一下:
- 概念模型:主要用于数据库设计;
- 逻辑模型:主要用于数据库管理系统的实现;
- 物理模型:描述数据在系统内部的表示方式和存取方法,它是对数据最底层的抽象。
用过多言语叙述它们显然不是我们的重点,我们现在就直奔主题,把里面涉及到的概念列举出来。
概念模型
在信息世界中主要会涉及以下概念:
(1)实体(entity)
实体:客观存在并可相互区别的事物。比如:一个学生、一个员工、一门课
(2)属性(attribute)
属性:实体所具有的某一特性。当然一个实体可以有若干个属性。比如:学生的学号、姓名、班级
(3)码(key)(主键 、 码键)
码:唯一标识实体的属性集,又或者说成:可以区分实体的最小属性组。比如:学生可以只用一个属性学号来区分,当然也可以用 姓名 + 班级 + … 等组合起来的属性集(组)来判断。
码是个很关键的概念,我们之后还会对其相关用法进行说明。
(4)实体型(entity type)
实体型:用实体名及其属性名集合来抽象和刻画同类实体。比如: 学生(学号,姓名,性别,出生年月,班级)
(5)实体集(entity set)
实体集:同一类型实体的集合。比如:全体学生
(6)联系(relationship)(关系)
联系:不同实体集之间的联系。这个联系分为一对一、一对多和多对多等。
联系也是个很关键的概念,这将是往后重要的逻辑关系(在项目中通常会有专人来负责产品的数据库设计)。
首先先来感受一下这些联系的概念:
① 如果对于实体集A中的每一个实体,实体集B中至多有一个(也可以没有)实体与之联系,反之亦然,则称实体集A与实体集B具有一对一联系。
② 如果对于实体集A中的每一个实体,实体集B中有n个实体(n ≥ 0)与之联系,反之,对于实体集B中的每一个实体,实体集A中至多只有一个实体与之联系,则称实体集A与实体集B具有一对多联系。
③ 如果对于实体集A中的每一个实体,实体集B中有n个实体(n ≥ 0)与之联系,反之,对于实体集B中的每一个实体,实体集A中也有m个实体(m ≥ 0)与之联系,则称实体集A与实体集B具有多对多联系。
举个例子感受一下:
① 一个老师只教这一门课,这门课又只由这名老师教,这就是一对一。
② 一个老师能教很多门课,而这些课又只由这一名老师教,这就是一对多。
③ 一个老师能教很多门课,同时这些课也会由多名老师教,这就是多对多。
接下来我们看另一个概念:
因为概念模型,它就是对信息世界的建模,所以它就应该有办法能够方便、准确地表示出上述常用概念,而表示它们的方法很多,最为常用和直观的是 实体-联系方法(Entity-RelationShip approach)(即:E-R图)。简单来说,这个E-R图就会包括实体、属性、实体之间的联系。
一篇文章了解ER图:数据库ER图基础概念整理
这部分内容实际上也很重要,因为ER图可以很好的展现项目数据需求,但这并不是我们要说的重点,我们继续回到正题。
逻辑模型
在数据库领域主要的逻辑数据模型有很多,在这里简单介绍一下层次模型。
层次模型是数据库系统中最早出现的数据模型,它用树形结构来表示各类实体以及实体间的联系。
感受一下:
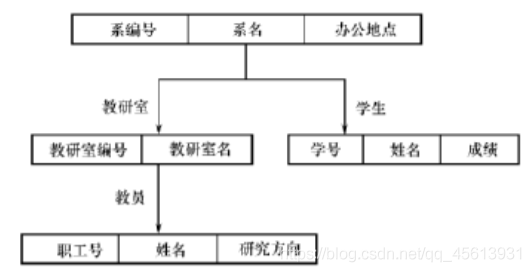
它的优缺点很明显:
(1)层次模型的数据结构简单清晰。
(2)层次数据库的查询效率高。
(3)查询子女结点必须通过双亲结点,如果一个结点具有多个双亲结点,代码编写将十分复杂。
其他的模型就不在这里叙述了。这种类似的模型虽然可以很直观地描述,具有良好的性能,但是随着数据的增多,应用环境的扩大,这种结构一定会变得越来越复杂,不利于管理人员的掌握。
因此,接下来要说的就是MySQL采用的关系模型。MySQL 是最流行的关系型数据库管理系统,在 WEB 应用方面 MySQL 是最好的 RDBMS(Relational Database Management System:关系数据库管理系统)应用软件之一。
关系型数据库
所谓的关系型数据库,是建立在关系模型基础上的数据库,借助于集合代数等数学概念和方法来处理数据库中的数据。这种所谓的"关系型"可以理解为"表格"的概念, 一个关系型数据库由一个或数个表格组成。
在继续学习 MySQL 数据库前,先叙述一些概念:
-
数据库: 数据库是一些关联表的集合。
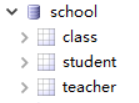
比如:上图中,school就是一个数据库,它里面有三个相关数据表。 -
数据表: 表是数据的矩阵。在一个数据库中的表看起来像一个简单的电子表格。

-
列(属性): 一列(数据元素) 包含了相同类型的数据。
-
行(元组、记录):一行是一组相关的数据。
-
主键(码、码键):主键是唯一的。一个数据表中只能包含一个主键,这个主键可能是某一属性也可能是某个属性组,它可以唯一确定一个元组(行)。你可以使用主键来查询数据。
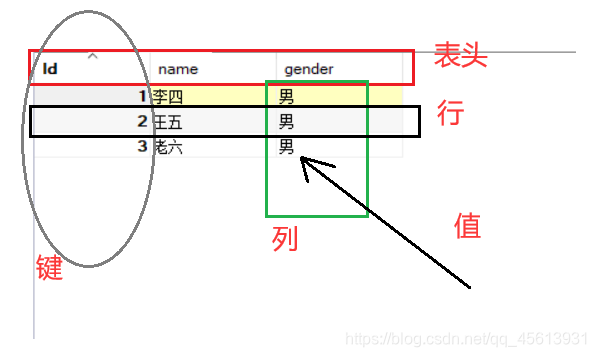
还有很多概念将会在之后用到的时候再说明。
关系数据结构
首先,先来介绍一下关系模型的数据结构。它的数据结构非常简单,只包含单一的数据结构——关系,也就是那一张张扁平的二维表。
在这里简单叙述一下关系数据结构的形式化定义。
(1)域:域是一组具有相同数据类型的值的集合。比如:自然数、整数、实数、{ 男,女 }、大于0且小于50的正整数。
(2)笛卡儿积:笛卡尔积是域上的一种集合运算。
它的完整定义是:给定一组域D1,D2,··· , Dn,允许其中某些域是相同的,D1,D2, ··· ,Dn的笛卡尔积为:
D1 x D2 x ··· x Dn = {(d1,d2,···,dn)| di ∈ Di,i = 1,2,···,n}
其中,每一个元素(d1,d2,···,dn)叫作一个n元组,或简称元组。元素中的每一个值 di 叫做一个分量。一个域允许的不同取值个数称为这个域的基数。
看个例子就明白了:
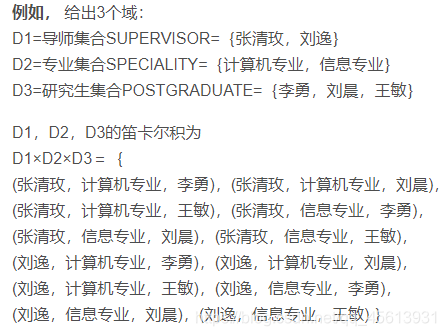
其中,每个()都是一个元组,()里的每个数据都是分量。
该笛卡儿积的基数为 2 x 2 x 3 = 12,也就是说,D1 x D2 X D3 共有12个元组,它们也就可以列成一张二维表。

而在这其中,有实际意义的才能被叫做是关系。没有实际意义的,那显然不是我们想要的。比如,我现在设定一个条件,就是一个老师只能教一个专业的学生,那上表中很多子集的存在根本就没有意义,因为它不符合实际。那么基于此,我们也就知道,关系是笛卡儿积的有限子集。
在关系中的某一属性组的值能唯一地标识一个元组,而其子集不能,则称该属性组为候选码。若一个关系有多个候选码,则选定其中一个为主码(主键)。
这里一定需要注意候选码的定义,比如:学生(id,姓名,性别…),只用 id 就可以唯一地标识一个元组,我们就不能也没必要 这么做:将 id + 姓名 作为候选码。
候选码的属性称为主属性,不包含在任何候选码中的属性称为非主属性或非码属性。
也就是说,在最简单的情况下,候选码只包含一个属性。在最极端的情况下,关系模式的所有属性是这个关系模式的候选码,称为全码。
还有一个容易混淆的概念,索引。
我们现在知道,主键能唯一地标识一个元组,而且整个表中只能有一个主键,那何为索引?
索引:使用索引可快速访问数据库表中的特定信息。索引是对数据库表中一列或多列的值进行排序的一种结构。
所以我们可以这样理解:
主键相当于是书籍的页码,我们根据页码就能找到这一页。
而索引相当于是书籍的目录,有了目录我们可以很快的知道这本书的基本内容和结构。
一篇文章读懂索引和主键:主键与索引的区别和联系
也许对这部分还会有些疑虑,不过不用担心,之后还会提到这些。
基本关系(基本表或基表)的性质
(注意:并不是所有基本表都会具有这6条性质。比如有的数据库产品是需要区分属性顺序和元组顺序)
① 列是同质的,即每一列中的分量都是同一类型的数据,来自同一个域。
② 不同的列可出自同一个域,称其中的每一列为一个属性,不同的属性要给予不同的属性名。比如:学生名和老师名都是人名,但我们要作出区分,所以不同的属性就给予了不同的属性名,分别称之为学生名和老师名。
③ 列的顺序无所谓,即列的次序可以任意交换。
④ 任意两个元组的候选码不能相同。(这个性质一定要注意,它能被选作候选码,就是因为它能唯一性地标识一个元组,现在两个元组的候选码如果相同,就无法判断出元组间的区别,所以这就不可能是候选码)
⑤ 行的顺序无所谓,即行的次序可以任意交换。
⑥ 分量必须取原子值,即每一个分量都必须是不可分的数据项。比如:学生选了很多门课,那现在想将课的相关数据存放在学生表里,那可能会想这么做:

但这种行为是不行的,因为其中的课程分量还是可分的数据项,即:我们不能让表中有表。那遇到类似的问题该怎么解决呢?经过之后的学习就能找到答案。
除此以外,还有很多规范性的东西,因为一旦数据出现了问题,造成的损失将会无法挽回,且相关数据的规范还远远不止这些,任何一个逻辑上处理数据的疏忽都有可能造成数据异常,但这部分内容就不详细去解读了,后续可以慢慢体会到相关规范。
综上所述关系模型要求关系必须是规范化的,即要求关系必须满足一定的规范条件。规范化的关系简称为范式(NF)。
推荐解读文章:数据库设计三大范式
关系的完整性
在关系模型中有三类完整性约束:实体完整性、参照完整性和用户定义的完整性。其中 实体完整性和参照完整性 是关系模型必须满足的完整性约束条件。
- 实体完整性:若属性(指一个或一组属性)A是基本关系R的主属性(即:候选码,可以作为主码的属性),则A不能取空值。所谓空值就是 “不知道” 或 “不存在” 或 “无意义” 的值。 道理很简单,既然能唯一性地标识一个元组,它肯定不能为空,否则也不满足主键(主码)定义。
在说下一个规则前,看一个情况:(主码用下划线标识)
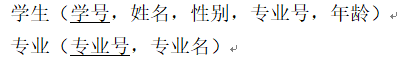
这两个关系之间存在着属性的引用,即学生关系引用了专业关系的主码“专业号”。也就是说,学生关系中的某个属性的取值需要参照专业关系的属性取值。
在这里引出一个概念:外码。
设 F 是基本关系 R 的一个或一组属性,但不是关系 R 的码,Ks 是基本关系 S 的主码。如果 F 与 Ks 相对应,则称 F 是 R 的外码,并称基本关系 R 为参照关系,基本关系 S 为被参照关系 或 目标关系。
就比如在上例中,学生关系的“专业号”属性与专业关系的主码“专业号”相对应,因此“专业号”属性是学生关系的外码。这里专业关系是被参照关系,学生关系为参照关系。
参照完整性就是定义外码与主码之间的引用规则。
- 参照完整性:若属性(或属性组)F 是基本关系 R 的外码,它与基本关系 S 的主码 Ks 相对应(基本关系 R 和 S 不一定是不同的关系),则对于 R 中每个元组在 F 上的值必须:① 或者取空值( F 的每个属性值均为空值) ② 或者等于 S 中某个元组的主码值。
比如:上例中,学生关系中每个元组的“专业号”属性只能取下面两类值:
① 空值,表示尚未给学生分配专业;
② 非空值,这时这个值必须是专业关系中某个元组的“专业号”值,否则代表着该学生分配到了一个不存在的专业中,就出现了问题。
用户定义的完整性就是针对某一具体关系数据库的约束条件,它反映了某一具体应用所涉及的数据必须满足的语义要求。比如:某个属性必须取唯一值、某个非主属性不能取空值等。
基本的关系操作
关系模型中常用的关系操作包括:增(insert)删(delete)改(update)查(query)。其中 查 是最主要的部分,因为可想而知 数据更新(增、删、改),增就去增加,删就去删除,改就去修改,不可能有多种多样的方式让其很复杂,而对于 数据查询,我们想要获取我们想要的数据,就需要花费一些精力了。
查询操作又可以分为 选择(select)、投影(project)、连接(join)、除(divide)、并(union)、差(except)、交(intersection)、笛卡儿积等。 其中,选择、投影、并、差、笛卡儿积 是5种基本操作。为什么是这5种?因为,其他操作都可以用上述5种基本操作中的某个或某几个来定义和导出,就像乘法可以用加法来定义和导出一样。
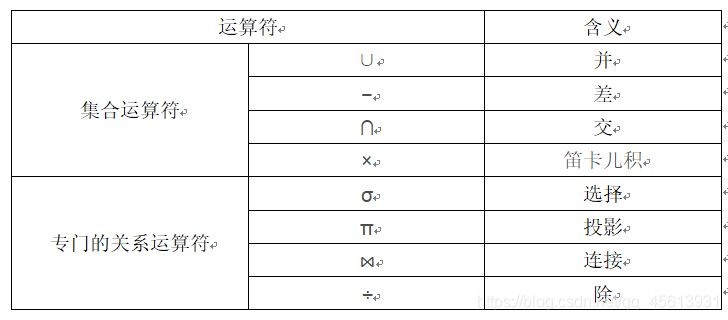
如果各位有 离散数学 的基础,那么接下来的运算将会很好理解。
传统的集合运算
传统的集合运算是二目运算,包括并、差、交、笛卡儿积 4 种运算。
设 关系 R 和 关系 S 具有相同的目 n(即两个关系都有 n 个属性),且相应的属性取自同一个域:

那么可以定义 并、差、交、笛卡儿积 运算如下:
① 并
其结果仍为 n 目关系,由属于 R 或 属于 S 的元组组成。

② 差
其结果仍为 n 目关系,由属于 R 而不属于 S 的所有元组组成。

③ 交
其结果仍为 n 目关系,由既属于 R 又属于 S 的元组组成。
交不属于基本操作,是因为 交 可以这么描述: R ∩ S = R -(R - S)

④ 笛卡儿积
笛卡儿积在上面演示过,在这里就不说明了。
专门的关系运算
这部分的概念其实都很严谨和繁琐,在这里就不进行过多的说明了,就把基本的用法记录下来。但要说的是,这部分很关键,在之后的SQL语句中,就会用到这些,而且如果能够熟练使用,在写SQL语句时就能加快查询速度。
① 选择
选择又称为限制。它是在关系 R 中选择满足给定条件的诸元组。
比如:
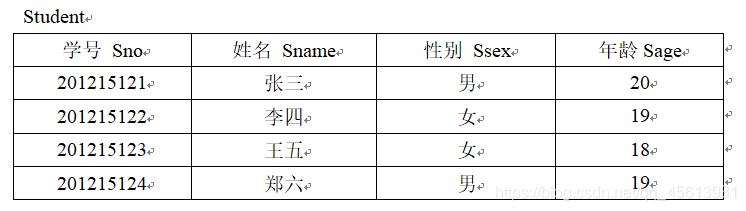
例1:查询女性学生:

输出结果是这样的:(其他例子的输出结果就不演示了)

例2:查询年龄小于20岁的学生:
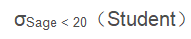
例3:查询年龄小于20岁的女性学生:
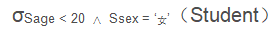
也就是说,选择σ 会选出满足条件的所有元组(行)。
② 投影
关系 R 上的投影是从 R 中选择出若干属性列组成新的关系。
比如:
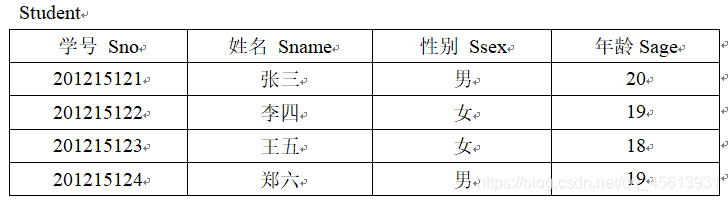
例1:查询学生的姓名和性别:

输出结果是这样的:
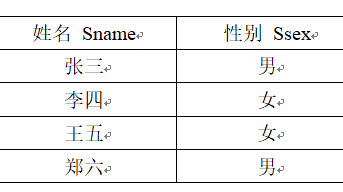
例2:查询女性学生的姓名:
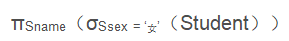
也就是说,投影 π 会选出若干属性列(或 满足一定条件的元组的若干属性列)。
③ 连接
连接也称为 θ 连接。它是从两个关系的笛卡儿积中选取属性间满足一定条件的元组。
首先,它有三种连接方式:非等值连接,等值连接,自然连接。
等值连接:它是从关系 R 与 S 的广义笛卡儿积中选择 A、B 属性值相等的那些元组。反之,选择那些属性不相等(即:需要满足一定条件)的那些元组的是非等值连接。
自然连接:一种特殊的等值连接。它要求两个关系中进行比较的分量必须是同名的属性组,并且在结果中把重复的属性列去掉。
举个例子就明白了:
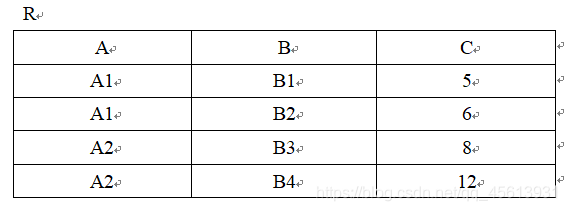
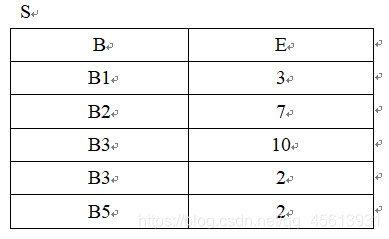
非等值连接:
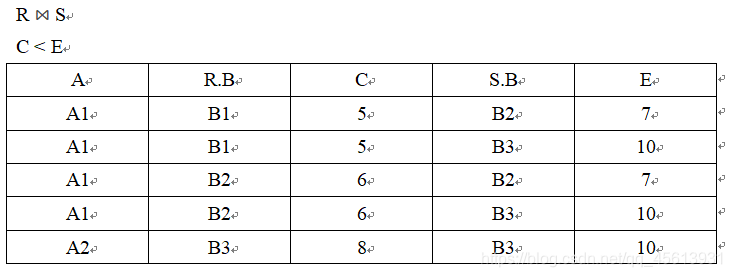
等值连接:

自然连接:
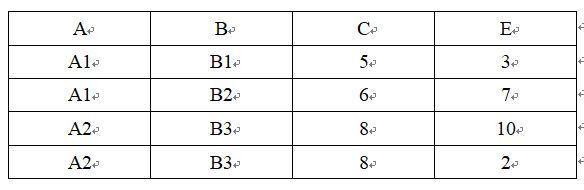
在等值连接(自然连接)的时候,我们可以看到 R 和 S 中某些元组是可能被舍弃的,这些被舍弃的元组被称为悬浮元组。
综上所述,我们就可以用这个新用法,加快查询速度:
例:寻找课程成绩在90分以上的学生姓名和学号:
(成绩存放在SC表)
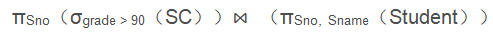
也就是说,如果两个表之间的属性有联系,可以考虑使用连接。
外连接
除此之外,在这里还有一些重要概念!
如果把悬浮元组也保存在结果关系中,而在其他属性上填空值(NULL),那么这种连接就叫做外连接。如果只保留左边关系 R 中的悬浮元组就叫做左外连接(left join),如果只保留右边关系 S 中的悬浮元组就叫做右外连接(right join)。
还拿上面的 R 和 S 举例。
外连接:
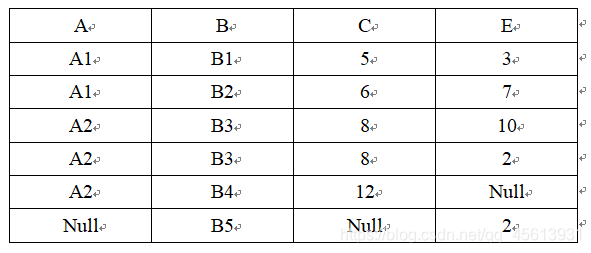
左外连接:
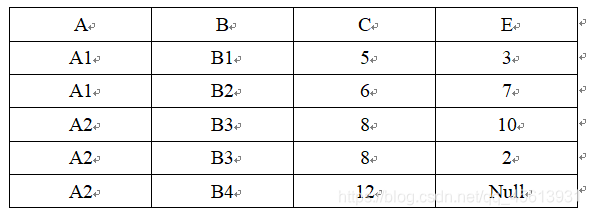
右外连接:
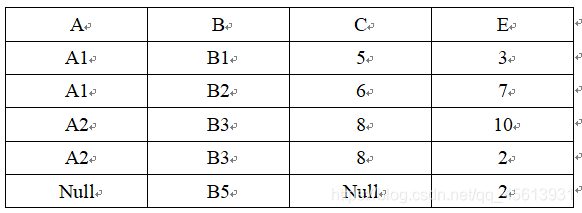
④ 除
为了方便理解,提出象集概念:
象集:它表示 R 中属性组 X 上值为 x 的诸元组在 Z 上分量的集合。
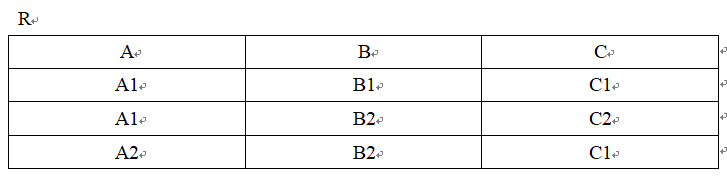
看个例子:
在关系 R 中,A 可以取4个值{ A1,A2,A3,A4 }
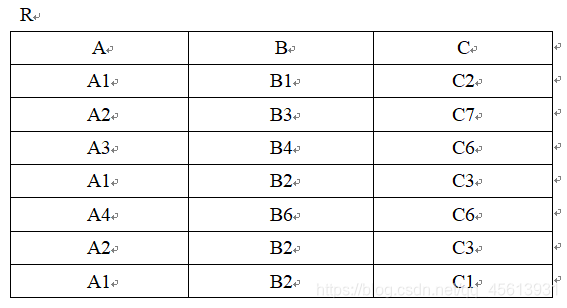
A1的象集为 {(B1,C2),(B2,C3),(B2,C1)};
A2的象集为 {(B3,C7),(B2,C3)};
A3的象集为 {(B4,C6)};
A4的象集为 {(B6,C6)};
现在看一下除法的定义:
设关系 R 除以关系 S 的结果为关系 T,则 T 包含所有在 R 但不在 S 中的属性及其值,且 T 的元组与 S 的元组的所有组合都在 R 中。

也就是说,根据上面给出的 R 和 S,除法的结果 T 包含所有在 R 但不在 S 中的属性及其值,也就是 上面例子 R 中的属性 A。而所谓的 T 的元组与 S 的元组的所有组合都在 R 中,就是说,最终结果 T 中得到的属性 A 组合 S 中的 B + C(在 R 中同名的属性)都会存在于 R 中。
比如:S 在(B,C)上的投影为{(B1,C2),(B2,C1),(B2,C3)}
显然在 R 中,只有 A1 的象集包含了 S 在(B,C)属性组上的投影。所以 R ÷ S = { A1 }

例:查询至少选修1号课程和3号课程的学生号码。
建立一个临时关系K:
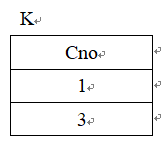
然后计算:

得到的结果就会是至少选修了1号课程和3号课程的学生号码Sno。
现在把上面所有内容组合起来就可以进行一系列运算了。在关系代数中,这些运算经有限次复合后形成的表达式称为关系代数表达式。
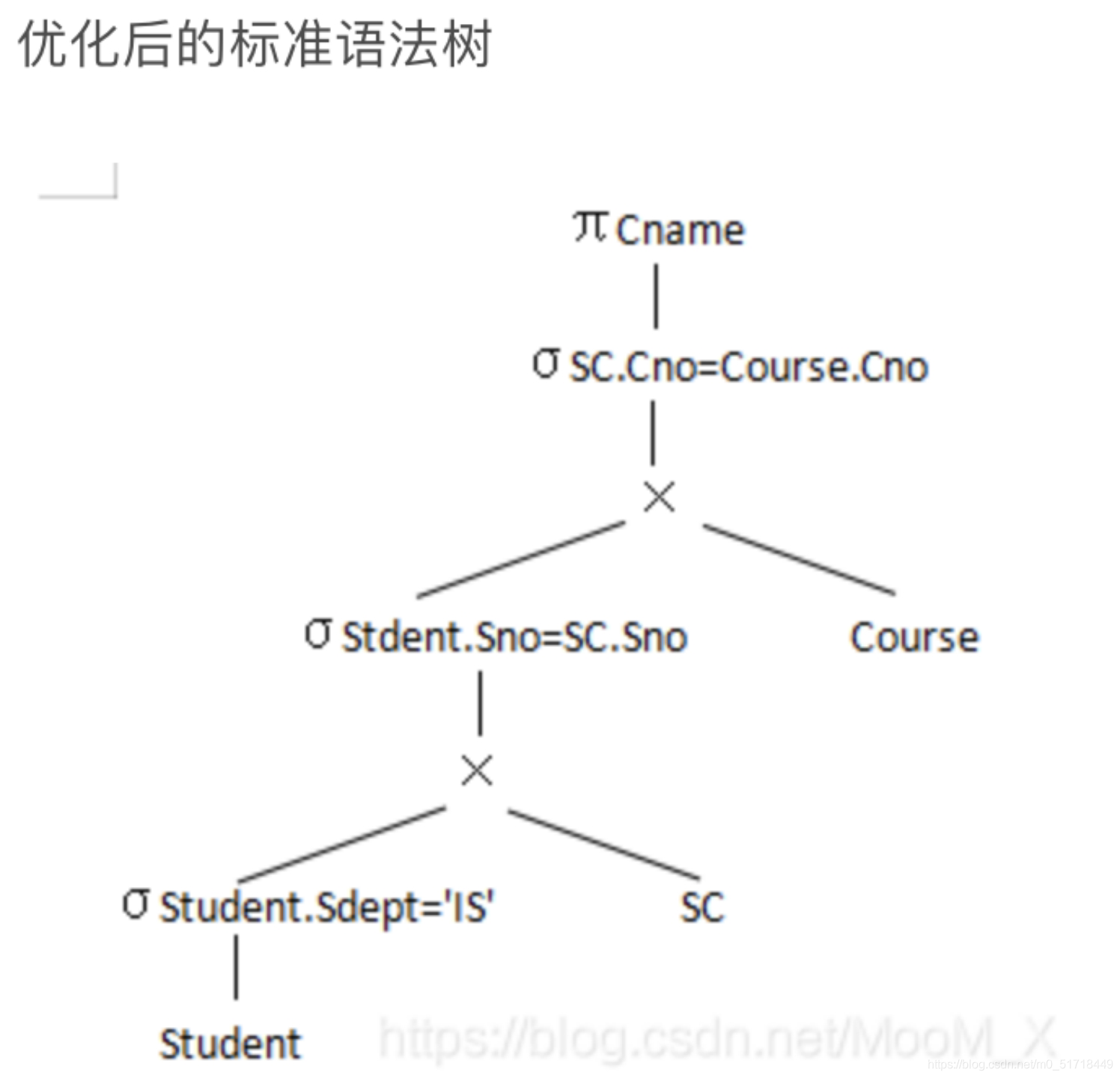
例:查询选修了全部课程的学生号码和姓名。

简单解析:
根据除法定义,我们得到了 SC 表中满足条件的学生学号 Sno 属性列,条件是该学生选课时需要选修 Course 表中所有课程(即 所有课程的编号 Cno)。
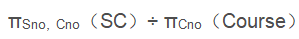
我们得到了满足条件的学生学号 Sno 属性列后,再去自然连接 Student 中的 Sno 和 Sname 属性列,就得到了同名属性值(Sno)相等的那些元组,就得到了答案。
有了这些基础后,将会方便后续 关系数据库标准语言SQL语句 的学习。
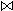









![[Python从零到壹] 五十七.图像增强及运算篇之图像锐化Roberts、Prewitt算子实现边缘检测](https://img-blog.csdnimg.cn/1dea2c88b4ec42f3ae67b7e8ada41bfd.png#pic_center)