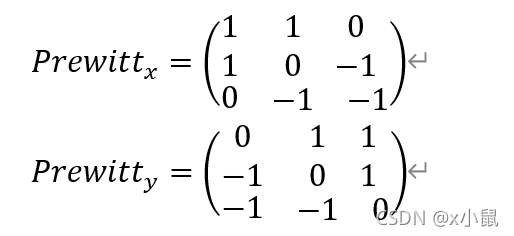机器学习MATLAB实现:Matlab-梯度Roberts算子、拉普拉斯算子、Sobel算子、Prewitt算子对图像进行锐化
欢迎大家来到安静到无声的《模式识别与人工智能(程序与算法)》,如果对所写内容感兴趣请看模式识别与人工智能(程序与算法)系列讲解 - 总目录,同时这也可以作为大家学习的参考。欢迎订阅,优惠价只需9.9元,请多多支持!
目录标题
- 机器学习MATLAB实现:Matlab-梯度Roberts算子、拉普拉斯算子、Sobel算子、Prewitt算子对图像进行锐化
- 1. 锐化
- 2. 梯度运算
- 3. 边缘检测的分类
- 4. Roberts算子
- 5. sobel算子
- 6. Prewitt算子
- 7. 拉普拉斯算子
- 8. matlab代码实现
1. 锐化
1.锐化(Sharpening) :图像在传输或变换过程中(如未聚焦好)、受到各种干扰而退化,典型的是图像模糊,而图像的判读和识别中,常需突出目标的轮廓或边缘信息。
2.边缘锐化:主要增强图像的轮廓边缘、细节( 灰度跳变部分),以突出图像中景物的边缘或纹理,形成完整的物体边界,使边缘和轮廓模糊的图像清晰,又叫空域高通滤波(俗称为勾边处理)。
从数学角度看,图像模糊相当于图像被平均或者积分,为实现图像的锐化,我们需要运用它的反运算“微分”——加强高频分量,实现轮廓清晰。
2. 梯度运算
设图像 f ( x , y ) f(x,y) f(x,y)为定义在点 ( x , y ) (x,y) (x,y)的梯度矢量为 G [ f ( x , y ) ] G[f(x,y)] G[f(x,y)]:
G [ f ( x , y ) ] = [ ∂ f ∂ x ∂ f ∂ y ] = [ ∂ f ∂ x ∂ f ∂ y ] ⊤ = ∇ f ( x , y ) \mathbf{G}[f(x, y)]=\left[\begin{array}{c} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{array}\right]=\left[\frac{\partial f}{\partial x} \frac{\partial f}{\partial y}\right]^{\top}=\nabla f(x, y) G[f(x,y)]=[∂x∂f∂y∂f]=[∂x∂f∂y∂f]⊤=∇f(x,y)
性质:
- 梯度的方向是在 f ( x , y ) f(x,y) f(x,y)的最大变化率方向
- 梯度的幅度用 G [ f ( x , y ) ] G[f(x,y)] G[f(x,y)]表示:
G [ f ( x , y ) ] = [ ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 ] 1 / 2 G[f(x, y)]=\left[\left(\frac{\partial f}{\partial x}\right)^{2}+\left(\frac{\partial f}{\partial y}\right)^{2}\right]^{1 / 2} G[f(x,y)]=[(∂x∂f)2+(∂y∂f)2]1/2
对于数字图像来说,梯度的求解从求偏导变成了相减
G [ f ( x , y ) ] = { [ f ( i , j ) − f ( i + 1 , j ) ] 2 + [ f ( i , j ) − f ( i , j + 1 ) ] 2 } 1 / 2 G[f(x, y)]=\left\{[f(i, j)-f(i+1, j)]^{2}+[f(i, j)-f(i, j+1)]^{2}\right\}^{1 / 2} G[f(x,y)]={[f(i,j)−f(i+1,j)]2+[f(i,j)−f(i,j+1)]2}1/2
简化为 G [ f ( x , y ) ] ≈ ∣ f ( i , j ) − f ( i + 1 , j ) ∣ + ∣ f ( i , j ) − f ( i , j + 1 ) ∣ G[f(x, y)] \approx|f(i, j)-f(i+1, j)|+|f(i, j)-f(i, j+1)| G[f(x,y)]≈∣f(i,j)−f(i+1,j)∣+∣f(i,j)−f(i,j+1)∣
3. 边缘检测的分类
(1)一阶导数的边缘算子
通过模板作为核与图像的每个像素点做卷积和运算,然后选取合适的阈值来提取图像的边缘。常见的有Roberts算子、Sobel算子和Prewitt算子。
(2)二阶导数的边缘算子
依据于二阶导数过零点,常见的有Laplacian 算子,此类算子对噪声敏感。
(3)其他边缘算子
前面两类均是通过微分算子来检测图像边缘,还有一种就是Canny算子,其是在满足一定约束条件下推导出来的边缘检测最优化算子。
4. Roberts算子
对于第二节所讲的数字梯度运算,我们将其公式改变为 G [ f ( x , y ) ] ≈ ∣ f ( i , j ) − f ( i + 1 , j + 1 ) ∣ + ∣ f ( i + 1 , j ) − f ( i , j + 1 ) ∣ G[f(x, y)] \approx|f(i, j)-f(i+1, j+1)|+|f(i+1, j)-f(i, j+1)| G[f(x,y)]≈∣f(i,j)−f(i+1,j+1)∣+∣f(i+1,j)−f(i,j+1)∣
这种交叉梯度我们称之为Roberts梯度。

5. sobel算子
基本思想:以待增强图像的任意象素 ( i , j ) (i,j) (i,j)为中心,截取一个 3 × 3 3×3 3×3的象素窗口,先分别计算窗口中心象素在 x x x, y y y方向的梯度:
S x = [ f ( i − 1 , j + 1 ) + 2 f ( i , j + 1 ) + f ( i + 1 , j + 1 ) ] − [ f ( i − 1 , j − 1 ) + 2 f ( i , j − 1 ) + f ( i + 1 , j − 1 ) ] S y = [ f ( i + 1 , j − 1 ) + 2 f ( i + 1 , j ) + f ( i + 1 , j + 1 ) ] − [ f ( i − 1 , j − 1 ) + 2 f ( i − 1 , j ) + f ( i − 1 , j + 1 ) ] \begin{aligned} &S_{x}=[f(i-1, j+1)+2 f(i, j+1)+f(i+1, j+1)]-[f(i-1, j-1)+2 f(i, j-1)+f(i+1, j-1)]\\&S_{y}=[f(i+1, j-1)+2 f(i+1, j)+f(i+1, j+1)]-[f(i-1, j-1)+2 f(i-1, j)+f(i-1, j+1)]\end{aligned} Sx=[f(i−1,j+1)+2f(i,j+1)+f(i+1,j+1)]−[f(i−1,j−1)+2f(i,j−1)+f(i+1,j−1)]Sy=[f(i+1,j−1)+2f(i+1,j)+f(i+1,j+1)]−[f(i−1,j−1)+2f(i−1,j)+f(i−1,j+1)]
增强后的 ( i , j ) (i,j) (i,j)的灰度: f ′ ( i , j ) = S x 2 + S y 2 f^{\prime}(i, j)=\sqrt{S_{x}^{2}+S_{y}^{2}} f′(i,j)=Sx2+Sy2
可以简化为: f ′ ( i , j ) = ∣ S x ∣ + ∣ S y ∣ f^{\prime}(i, j)={|S_{x}|+|S_{y}|} f′(i,j)=∣Sx∣+∣Sy∣
优点:
- 由于引入了加权平均,所以对图像中的随机噪声具有一定的平滑作用。
- 由于采用间隔两行或两列的差分,边缘两侧的象素得到增强,锐化图像的边缘显得粗而亮。
S x , S y Sx,Sy Sx,Sy可用卷积模板来实现 可用卷积模板来实现:
S x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] S y = [ − 1 − 2 − 1 0 0 0 1 2 1 ] S_{x}=\left[\begin{array}{ccc}-1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1\end{array}\right] \quad S_{y}=\left[\begin{array}{ccc}-1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1\end{array}\right] Sx= −1−2−1000121 Sy= −101−202−101
可见:其重点放在接近于模板中心的象素点
6. Prewitt算子
基本思想:与Sobel算子相同,方程的形式相同,但其中系数不同:
S x = [ − 1 0 1 − 1 0 1 − 1 0 1 ] S y = [ − 1 − 1 − 1 0 0 0 1 1 1 ] S p = S x 2 + S y 2 \begin{array}{c} S_{x}=\left[\begin{array}{ccc} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{array}\right] \quad S_{y}=\left[\begin{array}{ccc} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{array}\right] \\\\ S_{p}=\sqrt{S_{x}^{2}+S_{y}^{2}} \end{array} Sx= −1−1−1000111 Sy= −101−101−101 Sp=Sx2+Sy2
可见:与Sobel算子不同 ,其重点没有放在接近于模板中心的象素点。
7. 拉普拉斯算子
基本思想:拉普拉斯(Laplacian) 算子是 n 维欧几里德空间中的一个二阶微分算子。 ∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \nabla^{2} f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}} ∇2f=∂x2∂2f+∂y2∂2f 具有各向同性。
- 对于数字图像 f ( x , y ) f(x,y) f(x,y) ,其一阶导数为:
{ ∂ f ( i , j ) ∂ x = Δ x f ( i , j ) = f ( i , j ) − f ( i − 1 , j ) ∂ f ( i , j ) ∂ y = Δ y f ( i , j ) = f ( i , j ) − f ( i , j − 1 ) \left\{\begin{array}{l} \frac{\partial f(i, j)}{\partial x}=\Delta_{x} f(i, j)=f(i, j)-f(i-1, j) \\\\ \frac{\partial f(i, j)}{\partial y}=\Delta_{y} f(i, j)=f(i, j)-f(i, j-1) \end{array}\right. ⎩ ⎨ ⎧∂x∂f(i,j)=Δxf(i,j)=f(i,j)−f(i−1,j)∂y∂f(i,j)=Δyf(i,j)=f(i,j)−f(i,j−1) - f ( x , y ) f(x,y) f(x,y) ,其二阶导数为:
{ ∂ 2 f ( i , j ) ∂ x 2 = Δ x f ( i + 1 , j ) − Δ x f ( i , j ) = [ f ( i + 1 , j ) − f ( i , j ) ] − [ f ( i , j ) − f ( i − 1 , j ) ] = f ( i + 1 , j ) + f ( i − 1 , j ) − 2 f ( i , j ) ∂ 2 f ( i , j ) ∂ y 2 = f ( i , j + 1 ) + f ( i , j − 1 ) − 2 f ( i , j ) \left\{\begin{aligned} \frac{\partial^{2} f(i, j)}{\partial x^{2}} &=\Delta_{x} f(i+1, j)-\Delta_{x} f(i, j) \\ &=[f(i+1, j)-f(i, j)]-[f(i, j)-f(i-1, j)] \\ &=f(i+1, j)+f(i-1, j)-2 f(i, j) \\\\ \frac{\partial^{2} f(i, j)}{\partial y^{2}} &=f(i, j+1)+f(i, j-1)-2 f(i, j) \end{aligned}\right. ⎩ ⎨ ⎧∂x2∂2f(i,j)∂y2∂2f(i,j)=Δxf(i+1,j)−Δxf(i,j)=[f(i+1,j)−f(i,j)]−[f(i,j)−f(i−1,j)]=f(i+1,j)+f(i−1,j)−2f(i,j)=f(i,j+1)+f(i,j−1)−2f(i,j) - 拉普拉斯算子为: ∇ 2 f ( i , j ) = Δ x 2 f ( i , j ) + Δ y 2 ( i , j ) = f ( i + 1 , j ) + f ( i − 1 , j ) + f ( i , j + 1 ) + f ( i , j − 1 ) − 4 f ( i , j ) = − 5 { f ( i , j ) − 1 5 [ f ( i + 1 , j ) + f ( i − 1 , j ) + f ( i , j + 1 ) + f ( i , j − 1 ) + f ( i , j ) ] } \begin{aligned} \nabla^{2} f(i, j) &=\Delta_{x}^{2} f(i, j)+\Delta_{y}^{2}(i, j) \\ &=f(i+1, j)+f(i-1, j)+f(i, j+1)+f(i, j-1)-4 f(i, j) \\ &=-5\left\{f(i, j)-\frac{1}{5}[f(i+1, j)+f(i-1, j)+f(i, j+1)+f(i, j-1)+f(i, j)]\right\} \end{aligned} ∇2f(i,j)=Δx2f(i,j)+Δy2(i,j)=f(i+1,j)+f(i−1,j)+f(i,j+1)+f(i,j−1)−4f(i,j)=−5{f(i,j)−51[f(i+1,j)+f(i−1,j)+f(i,j+1)+f(i,j−1)+f(i,j)]}
其中,Laplacian算子四邻域模板如下所示:
H = [ 0 − 1 0 − 1 4 − 1 0 − 1 0 ] \mathrm{H}=\left[\begin{array}{ccc} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{array}\right] H= 0−10−14−10−10
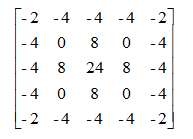
Laplacian算子八邻域模板如下所示
H = [ − 1 − 1 − 1 − 1 8 − 1 − 1 − 1 − 1 ] \mathrm{H}=\left[\begin{array}{ccc} -1 & -1 & -1 \\ -1 & 8& -1 \\ -1 & -1 & -1 \end{array}\right] H= −1−1−1−18−1−1−1−1
可见:
- 当邻域内像素灰度相同时,模板的卷积运算结果为0;
- 当中心像素灰度高于邻域内其他像素的平均灰度时,模板的卷积运算结果为正数;
- 当中心像素的灰度低于邻域内其他像素的平均灰度时,模板的卷积为负数。对卷积运算的结果用适当的衰弱因子处理并加在原中心像素上,就可以实现图像的锐化处理。
8. matlab代码实现
clc;clear all;
img = imread('C:\Users\lihuanyu\Desktop\opencv\image\lena256.bmp');
figure;
imshow(img),title("原图像");
[ROW,COL] = size(img);
img = double(img);
new_img = zeros(ROW,COL); %新建画布
%定义robert算子
roberts_x = [1,0;0,-1];
roberts_y = [0,-1;1,0];
for i = 1:ROW - 1for j = 1:COL - 1funBox = img(i:i+1,j:j+1);G_x = roberts_x .* funBox;G_x = abs(sum(G_x(:)));G_y = roberts_y .* funBox;G_y = abs(sum(G_y(:)));roberts_xy = G_x * 0.5 + G_y * 0.5;new_img(i,j) = roberts_xy;end
end
figure(2);
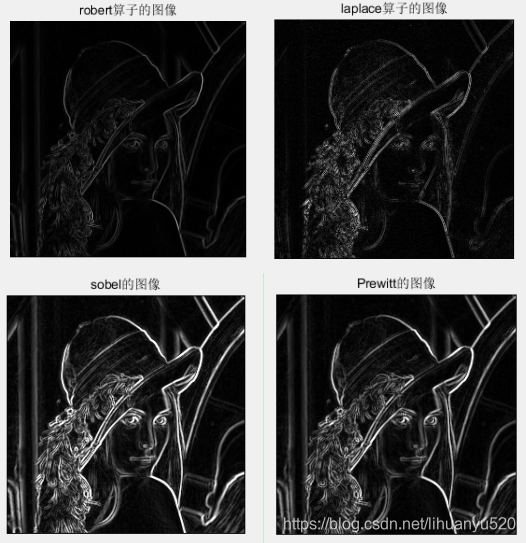
imshow(new_img/255),title("robert算子的图像");
% 定义laplace算子
laplace = [0,1,0;1,-4,1;0,1,0];
for i = 1:ROW - 2for j = 1:COL - 2funBox = img(i:i+2,j:j+2);G = laplace .* funBox;G = abs(sum(G(:)));new_img(i+1,j+1) = G;end
end
figure(3)
imshow(new_img/255),title("laplace算子的图像");
%定义sobel算子
sobel_x = [-1,0,1;-2,0,2;-1,0,1];
sobel_y = [-1,-2,-1;0,0,0;1,2,1];
for i = 1:ROW - 2for j = 1:COL - 2funBox = img(i:i+2,j:j+2);G_x = sobel_x .* funBox;G_x = abs(sum(G_x(:)));G_y = sobel_y .* funBox;G_y = abs(sum(G_y(:)));sobelxy = G_x * 0.5 + G_y * 0.5;new_img(i+1,j+1) = sobelxy;end
end
figure(4);
imshow(new_img/255),title("sobel的图像");
%定义Prewitt算子
sobel_x = [-1,0,1;-1,0,1;-1,0,1];
sobel_y = [-1,-1,-1;0,0,0;1,1,1];
for i = 1:ROW - 2for j = 1:COL - 2funBox = img(i:i+2,j:j+2);G_x = sobel_x .* funBox;G_x = abs(sum(G_x(:)));G_y = sobel_y .* funBox;G_y = abs(sum(G_y(:)));sobelxy = G_x * 0.5 + G_y * 0.5;new_img(i+1,j+1) = sobelxy;end
end
figure(5);
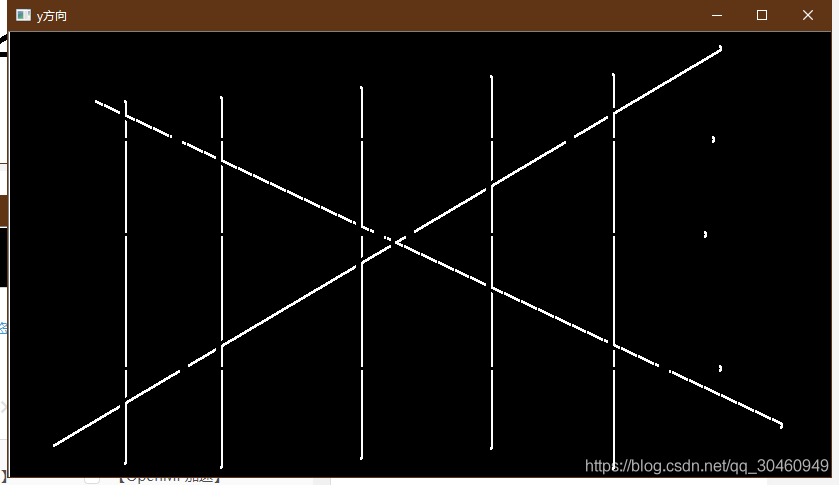
imshow(new_img/255),title("Prewitt的图像");
原图:

结果:




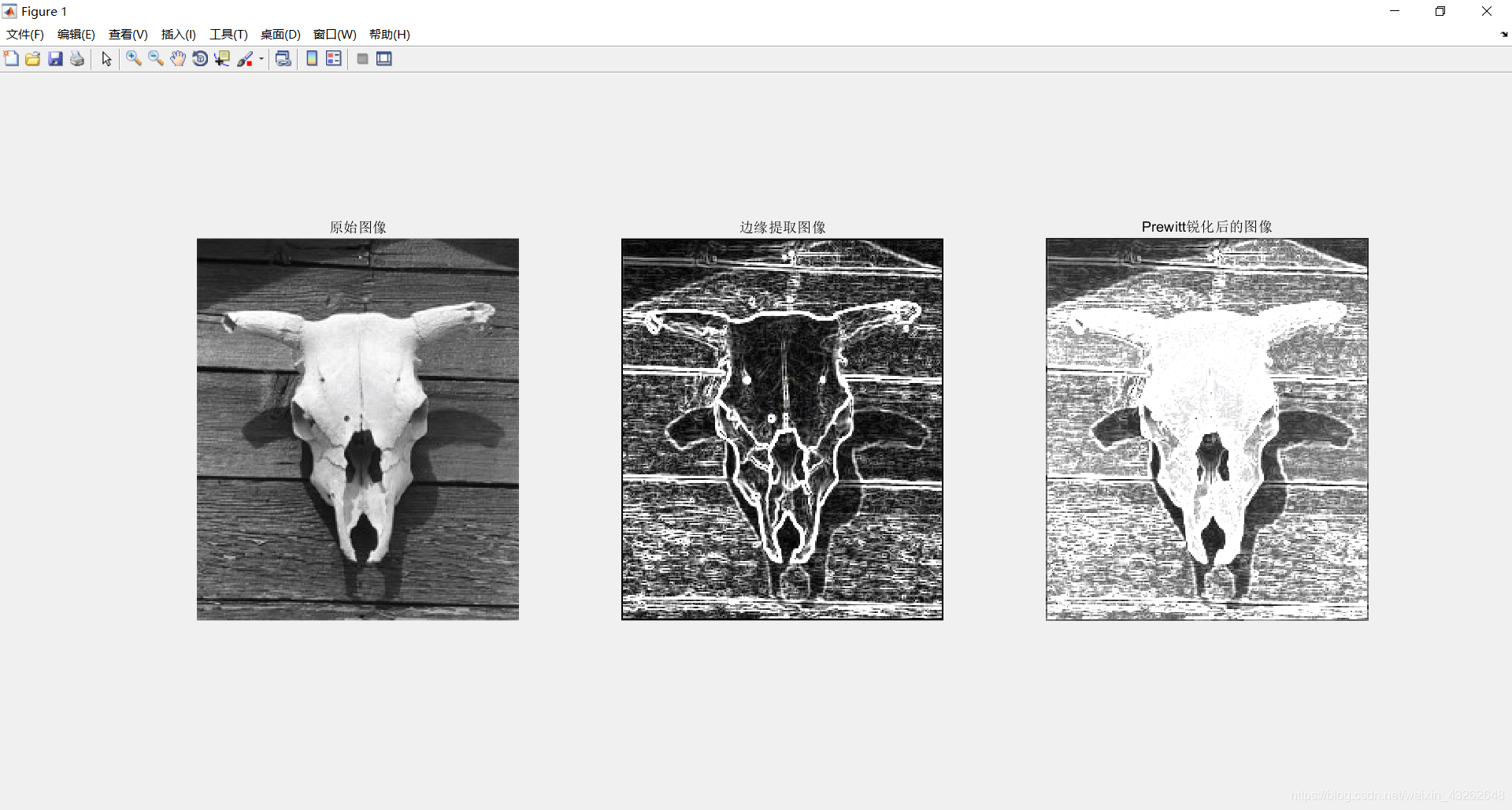

![[Python从零到壹] 五十七.图像增强及运算篇之图像锐化Roberts、Prewitt算子实现边缘检测](https://img-blog.csdnimg.cn/1dea2c88b4ec42f3ae67b7e8ada41bfd.png#pic_center)