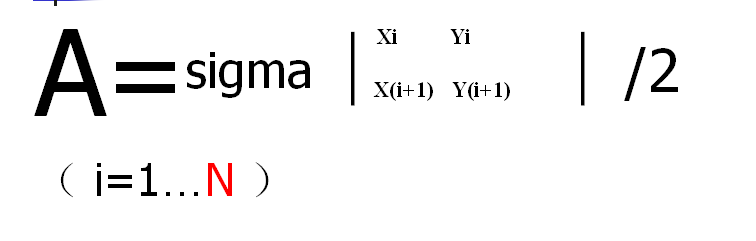皮克定理和任意多边形的面积公式

article/2025/9/6 2:16:50

1. 叉乘：

若： $\vec{a}=(x_1,y_1)$ ， $\vec{b}=(x_2,y_2)$ ，则： $\vec{a}\times \vec{b}=(x_1*y_2~-~x_2*y_1)\vec{z}$

而： $|\vec{a}\times\vec{b}|=|x_1*y_2~-~x_2*y_1|=|\vec{a}|*|\vec{b}|*sin(\theta )$

则： $S_{\bigtriangleup }=1/2~*~|\vec{a}|*|\vec{b}|*sin(\theta )=1/2~*~|x_1*y_2~-~x_2*y_1|$

$S_{\bigtriangleup }$ 为三角形面积，建议百度叉乘的几何意义

2. 皮克公式：

$\dpi{120} \dpi{150} S_{ polygon }=n~+~s/2~-1$

即：多边形面积 S = 多边形内整数点的个数 n + 多边形边上整数点的个数 / 2 - 1

注：多边形的顶点坐标必须是整数

3. 线段上整数点的个数：

gcd(线段在x轴的投影长，线段在y轴的投影长) + 1

注：线段的两端点坐标都必须是整数

简单证明：

设点 A(x1,y1)，B(x2,y2)，且 x1 <= x2，y1 <= y2（方便后面的叙述）

现在以 A 点为原点建立直角坐标系，线段 AB 在 x 轴的投影长为：a = x2 - x1，在 y 轴的投影长为：b = y2 - y1，那么线段 AB 的方程为 y = bx/a (0 =< x <= a)，设 g = gcd(a,b)，b' = b/g，a' = a/g；同样有：y = b'x/a'，此时 a' 与 b' 互质，若想 y 为整数，那么必有 x = ka'；由于 x 属于 [0，a]，那么这样的 x 有：a / a' = g 个，再加上原点这一个，证毕！！！

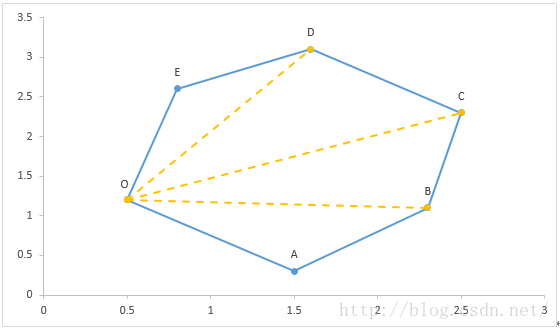
4. 任意多边形的面积

皮克公式有一定的局限性；上文给出了三角形的公式，对于只知道顶点坐标的情况下，我们可以将 n 边形化成 n-2 个三角形

$S_{polygon}=S_{\bigtriangleup OAB}+S_{\bigtriangleup OBC}+S_{\bigtriangleup OCD}+S_{\bigtriangleup ODE}$ ，依次用叉乘算出每个三角形的面积，求和就得到了多边形的面积，计算 $S_{\bigtriangleup OBC}$ 时用到了 $S_{\bigtriangleup OAB}$ 的边向量 $\underset{OB}{\rightarrow}$ ，于是化简可以得到多边形的面积公式(点的坐标必须是顺时针或逆时针依次给出的)：

$\large S=\frac{1}{2}|\sum_{1}^{n-1}(x[i]*y[i+1]-x[i+1]*y[i])~+~x[n]*y[1]-x[1]*y[n]|$

读者可能会想如果点的坐标不是按顺序依次给出的又该怎么办呢？

（1）所给多边形为凹包：

如果点不是按照顺序依次给出的，那么所构成的多边形一定不唯一（画画就明了），所以点一定是按顺序给出的

（2）所给多边形为凸包：

我们可以先将点按极角排序，就可套用公式了，（凹包的点极角排序后多边形的顶点不是依次有序的）

ps：极角排序

ps：线性代数知识解释公式来历

5. 应用：

（1）HDU 1705 - Count the grid

题意：

给你三个点，求三个点组成的三角形内有多少个整数点，不算边上的，也就是求皮克公式中的n

代码：

// n = S - s/2 + 1
#include <cmath>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long double ld;
int main()
{int x1,y1,x2,y2,x3,y3;while(cin>>x1>>y1>>x2>>y2>>x3>>y3){if(x1==0&&y1==0&&x2==0&&y2==0&&x3==0&&y3==0)break;int a1 = x2-x1,b1 = y2-y1;int a2 = x3-x1,b2 = y3-y1; int S = abs(a1*b2-b1*a2)/2;  //要加绝对值int s = __gcd(abs(x1-x2),abs(y1-y2))+1;s += __gcd(abs(x3-x2),abs(y3-y2))+1;s += __gcd(abs(x1-x3),abs(y1-y3))+1-3;//重复计算了3个顶点cout<<S - s/2 + 1<<endl;}return 0;
}

（2）2018年牛客多校算法寒假训练营练习比赛

代码：

#include <cmath>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef long double ld;
int main()
{int x1,y1,x2,y2,x3,y3;while(cin>>x1){if(x1==-1) break;cin>>y1>>x2>>y2>>x3>>y3;int a1 = x2-x1,b1 = y2-y1;int a2 = x3-x1,b2 = y3-y1;double S = abs((double)a1*b2-b1*a2)/2.0;int ab = __gcd(abs(x1-x2),abs(y1-y2))+1;int bc= __gcd(abs(x3-x2),abs(y3-y2))+1;int ac= __gcd(abs(x1-x3),abs(y1-y3))+1;int s = ab + bc + ac - 3;printf("%.1f ",S);printf("%lld %d %d %d\n",(ll)S-s/2+1,ab-2,bc-2,ac-2);}return 0;
}

（3） HDU 2036 多边形的面积

代码：

#include <cmath>
#include <cstdio>
#include <iostream>
using namespace std;
struct point
{int x,y;
}p[150];
int main()
{int n;while(cin>>n&&n){for(int i=0;i<n;++i)cin>>p[i].x>>p[i].y;int ans = p[n-1].x*p[0].y - p[n-1].y*p[0].x;for(int i=0;i<n-1;++i)ans += p[i].x*p[i+1].y - p[i].y*p[i+1].x;printf("%.1f\n",abs(ans)*1.0/2.0);}return 0;
}

（4）牛客网-简单多边形

题意：

判断顶点坐标是按什么顺序给出的

题解：

根据叉乘的几何意义，顺时针计算，结果为负，逆时针结果为正

代码：

#include <cmath>
#include <iostream>
using namespace std;
int x[110];
int y[110];
int main()
{int n;cin>>n;for(int i=1;i<=n;++i)cin>>x[i]>>y[i];int ans = 0;for(int i=1;i<n;++i){ans += x[i]*y[i+1] - x[i+1]*y[i];}ans += x[n]*y[1]-x[1]*y[n];if(ans>0) cout<<"counterclockwise";else cout<<"clockwise";return 0;
}