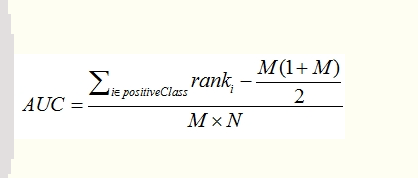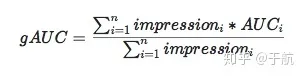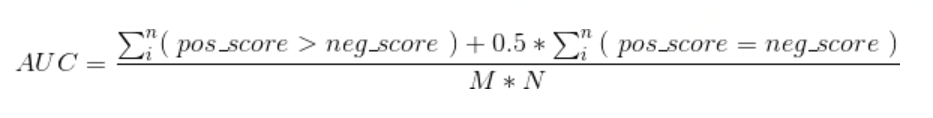深入理解AUC
AUC是什么
auc是roc曲线的面积,常用来评价二分类系统的好坏。
AUC如何计算
对于二分类问题,预测模型会对每一个预测样本一个得分p,然后选取一个阈值t,当 p > t p>t p>t时,样本预测为正,当 p < = t p<=t p<=t时样本预测为负。根据样本自身的标签值和模型预测的标签值,我们可以把样本划分为四个部分。分别是TP、FP、TN、FN。如下图所示:

随着阈值t选取的不同,这四类样本的比例各不相同。定义TPR(真正例率)和FPR(假正例率)分别如下:
T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP
F P R = F P F P + T N FPR=\frac{FP}{FP+TN} FPR=FP+TNFP
- TPR的意义是所有真实类别为1的样本中,预测类别为1的比例
- FPR的意义是所有真实类别为0的样本中,预测类别为1的比例
当阈值t发生变化时,TPR和FPR会随之变化。我们将TPR和FPR写成关于t的变量形式。定义 N + ( t ) N_{+}(t) N+(t)和 N − ( t ) N_{-}(t) N−(t)分别为得分大于 t t t的样本中正负样本的数目, N + N_{+} N+和 N − N_{-} N−为总的正负样本数目,则:
T P R ( t ) = N + ( t ) N + TPR(t)=\frac{N_{+}(t)}{N_{+}} TPR(t)=N+N+(t)
F P R ( t ) = N − ( t ) N − FPR(t)=\frac{N_{-}(t)}{N_{-}} FPR(t)=N−N−(t)
以TPR为横轴,FPR为纵轴,随着阈值t的变化,点 ( T P R , F P R ) (TPR,FPR) (TPR,FPR)会在坐标轴上画出一条曲线,这条曲线就是ROC曲线。
显然,如果模型是随机的,模型得分对正负样本没有区分性,那么得分大于t的样本中正负样本的比例应该和总的正负样本比例基本一致。也就是说
N + ( t ) N − ( t ) = N + N − \frac{N_{+}(t)}{N_{-}(t)}=\frac{N_{+}}{N_{-}} N−(t)N+(t)=N−N+
从上式可以看出此时ROC曲线是一条直线。
反之,如果模型的区分性非常理想,也就是说正负样本的得分可以完全分开,所有的正样本都比负样本得分高,此时ROC曲线表现为「字形。
实际的模型ROC曲线则是一条上凸的曲线,介于随机和理想的ROC曲线之间。二ROC曲线的面积即为AUC!
A U C = ∫ t = ∞ + ∞ y ( t ) d x ( t ) AUC=\int _{t=\infty}^{+\infty}y(t)dx(t) AUC=∫t=∞+∞y(t)dx(t)
这里的 x x x和 y y y分别是FPR和TPR,是ROC曲线的横纵坐标。
ROC曲线上有几个值得关注的点:
- (0,1):此时 F P R = 0 FPR=0 FPR=0, T P R = 1 TPR=1 TPR=1模型最好,混淆矩阵是对角矩阵
- (0,0): F P R = 0 FPR=0 FPR=0, T P R = 0 TPR=0 TPR=0,此时当 t ≥ 1 t \ge 1 t≥1时取到,即样本预测全部为负样本,混淆矩阵第一行全为0
- (1,1): F P R = 1 FPR=1 FPR=1, T P R = 1 TPR=1 TPR=1,此时当 t ≤ 0 t \le 0 t≤0时取到,即样本预测全部为正样本,混淆矩阵第二行全为0
AUC的概率解释
AUC常常被用来作为模型排序好坏的指标,原因在于AUC可以看做随机从正负样本中选取一对正负样本,其中正样本的得分大于负样本的概率!考虑随机取得这对正负样本中,负样本得分在 [ t , t + Δ t ] [t,t+\Delta t] [t,t+Δt]之间的概率为
P ( t ≤ s − < t + Δ t ) = P ( s − > t ) − P ( s − > t + Δ t ) P(t \le s_{-} < t+\Delta t)=P(s_{-}>t)-P(s_{-}>t+\Delta t) P(t≤s−<t+Δt)=P(s−>t)−P(s−>t+Δt)
= N − ( t ) − N − ( t + Δ t ) N − = x ( t ) − x ( t + Δ t ) = − Δ x ( t ) =\frac{N_{-}(t)-N_{-}(t+\Delta t)}{N_{-}}=x(t)-x(t+\Delta t)=-\Delta x(t) =N−N−(t)−N−(t+Δt)=x(t)−x(t+Δt)=−Δx(t)
如果 Δ t \Delta t Δt很小,那么该正样本得分大于该负样本的概率为
P ( s + > s − ∣ t ≤ s − < t + Δ t ) ≈ P ( s + > t ) = N + ( t ) N + = y ( t ) P(s_{+}>s_{-}|t \le s_{-} < t+\Delta t) \approx P(s_{+}>t)=\frac{N_{+}(t)}{N_{+}}=y(t) P(s+>s−∣t≤s−<t+Δt)≈P(s+>t)=N+N+(t)=y(t)
所以, P ( s + > s − ) = ∑ P ( t ≤ s − < t + Δ t ) P ( s + > s − ∣ t ≤ s − < t + Δ t ) = − ∫ t = − ∞ ∞ y ( t ) d x ( t ) = ∫ t = ∞ − ∞ y ( t ) d x ( t ) = A U C P(s_{+}>s_{-})=\sum P(t \le s_{-} < t+ \Delta t)P(s_{+}>s_{-}|t \le s_{-} < t+ \Delta t)=-\int_{t=-\infty}^{\infty}y(t)dx(t)=\int_{t=\infty}^{-\infty}y(t)dx(t)=AUC P(s+>s−)=∑P(t≤s−<t+Δt)P(s+>s−∣t≤s−<t+Δt)=−∫t=−∞∞y(t)dx(t)=∫t=∞−∞y(t)dx(t)=AUC。
这个积分表示为随机在样本里面取一对正负样本,正样本的得分大于负样本的概率。
AUC的排序特性
根据上面的概率解释,AUC实际上在说一个模型把正样本排在负样本前面的概率!所以AUC常用在排序场景的模型评估,比如搜索和推荐等场景!这个解释还表明,如果将所有的样本得分加上一个额外的常数并不改变这个概率,因此AUC不变。因此,在广告等需要绝对的点击率场景下,AUC并不适合作为评估指标,而是用logloss等指标。
AUC对正负样本比例不敏感
利用概率解释还可以得到AUC另一个性质:对正负样本比例不敏感。在训练模型的时候,如果正负样本差异较大,我们经常会对正样本进行过采样或者对负样本进行下采样。当一个模型训练完了之后,用负样本下采样后的测试集计算出来的AUC和未采样的测试集计算的AUC基本一致,或者说前者是后者的无偏估计!对于阈值t来说,党对正样本或者负样本进行均衡采样时,大于t或者小于t的样本是等比例变化的,即 k ∗ N + ( t ) k ∗ N + = N + ( t ) N + \frac{k*N_{+}(t)}{k*N_{+}}=\frac{N_{+}(t)}{N_{+}} k∗N+k∗N+(t)=N+N+(t), k ∗ N − ( t ) k ∗ N − = N − ( t ) N − \frac{k*N_{-}(t)}{k*N_{-}}=\frac{N_{-}(t)}{N_{-}} k∗N−k∗N−(t)=N−N−(t)。无论哪种情况,积分式大小不发生变化。
相比于其他评估指标,例如准确率、召回率和F1值,负样本下采样相当于只将一部分真实的负例排除掉了,然而模型并不能准确地识别出这些负例,所以用下采样后的样本来评估会高估准确率;因为采样只对负样本采样,正样本都在,所以采样对召回率并没什么影响。这两者结合起来,最终导致高估F1值!
AUC的计算
AUC可以直接根据ROC曲线,利用梯形积分进行计算。此外,还有一个比较有意思的是,可以 利用AUC与Wilcoxon-Mann-Whitney测试的U统计量的关系,来计算AUC。这可以从AUC的概率意义推导而来。
假设我们将测试集的正负样本按照模型预测得分从小到大排序,对于第 j j j个正样本,假设它的排序为 r j r_{j} rj,那么说明排在这个正样本前面的总样本有 r j − 1 r_{j}-1 rj−1个,其中正样本有 j − 1 j-1 j−1个,所以排在前面的负样本个数为 r j − j r_{j}-j rj−j个。也就是说,对于第 j j j个正样本来说,其得分比随机取的一个负样本大的概率为 ( r j − j ) / N − (r_{j}-j)/N_{-} (rj−j)/N−,其中 N − N_{-} N−是总的负样本数目。所以,平均下来,随机取的正样本得分比负样本大的概率为
1 N ∑ j = 1 N + ( r j − j ) / N − = ∑ j = 1 N + r j − N + ( N + + 1 ) / 2 N + N − \frac{1}{N}\sum_{j=1}^{N_{+}}(r_j-j)/N_-=\frac{\sum_{j=1}^{N_+}r_j-N_+(N_++1)/2}{N_+N_-} N1j=1∑N+(rj−j)/N−=N+N−∑j=1N+rj−N+(N++1)/2
所以 A U C = ∑ j = 1 N + r j − N + ( N + + 1 ) / 2 N + N − AUC=\frac{\sum_{j=1}^{N_+}r_j-N_+(N_++1)/2}{N_+N_-} AUC=N+N−∑j=1N+rj−N+(N++1)/2
一个更加简单的解释:
将得分从小到大排序,阈值t从 + ∞ +\infty +∞到 − ∞ -\infty −∞变化。当阈值右边增加一个正样本时, T P TP TP增加一个,这个正样本对面积的贡献率为 1 N + r j − j N − \frac{1}{N_+} \frac{r_j-j}{N_{-}} N+1N−rj−j,将所有的正样本贡献率加起来即是ROC面积。即为 ∑ j = 1 N + 1 N + r j − j N − = ∑ j = 1 N + r j − N + ( N + + 1 ) / 2 N + N − \sum_{j=1}^{N_+}\frac{1}{N_+} \frac{r_j-j}{N_{-}}=\frac{\sum_{j=1}^{N_+}r_j-N_+(N_++1)/2}{N_+N_-} ∑j=1N+N+1N−rj−j=N+N−∑j=1N+rj−N+(N++1)/2。
AUC计算的其它形式
A U C = ∑ i = 1 N + ∑ j = 1 N − δ ( s i + − s j − ) N + N − AUC=\frac{\sum_{i=1}^{N_+}\sum_{j=1}^{N_-}\delta(s_i^+-s_j^-)}{N_+N_-} AUC=N+N−∑i=1N+∑j=1N−δ(si+−sj−)
其中当 x > 0 x>0 x>0时 δ ( x ) = 1 δ(x)=1 δ(x)=1,当 x < 0 x<0 x<0时, δ ( x ) = 0 \delta(x)=0 δ(x)=0,我们将 δ \delta δ函数“软化”,即用 s i g m o i d sigmoid sigmoid函数来替代,那么 A U C AUC AUC就是可作为直接优化目标来进行微分。
s o f t A U C = ∑ i = 1 N + ∑ j = 1 N − σ ( s i + − s j − ) N + N − softAUC=\frac{\sum_{i=1}^{N_+}\sum_{j=1}^{N_-}\sigma(s_i^+-s_j^-)}{N_+N_-} softAUC=N+N−∑i=1N+∑j=1N−σ(si+−sj−)
AUC的优化
采用极大似然估计对应的损失函数是logloss,因此极大似然估计的优化目标并不是AUC。在一些排序场景下,AUC比logloss更贴近目标,因此直接优化AUC可以达到比极大似然估计更好的结果。 实际上,pairwise的目标函数就可以看做一种对AUC的近似。因为损失函数都是作用与正负样本得分差之上! 例如,
| 类别 | 优化目标 |
|---|---|
| rank-SVM | m a x ( 0 , − s + + s − + Δ ) max(0, -s_++s_-+\Delta) max(0,−s++s−+Δ) |
| rank-net | l o g ( 1 + e x p ( − ( s + − s − ) ) ) log(1+exp(-(s_+-s_-))) log(1+exp(−(s+−s−))) |
| 指数损失 | e x p ( − ( s + − s − ) ) exp(-(s_+-s_-)) exp(−(s+−s−)) |
| TOP损失 | ∑ s m a x ( 0 , − s c + s + Δ ) \sum_smax(0,-s_c+s+\Delta) ∑smax(0,−sc+s+Δ) |
显然,这些损失函数都是对 s + < s − s_+<s_- s+<s−的正负样本对进行惩罚!此外,也有一些其它对AUC近似度更好的损失函数,例如
E [ ( 1 − w T ( s + − s − ) ) 2 ] = 1 n + n − ∑ i = 1 n + ∑ j = 1 n − ( 1 − w T ( s i + − s j − ) ) 2 \mathbf{E} \left[ (1-w^T(s_+ - s_-))^2 \right] \\ = \frac{1}{n_+n_-} \sum_{i=1}^{n_+} \sum_{j=1}^{n_-} (1-w^T(s_{i}^+ - s_{j}^-))^2 E[(1−wT(s+−s−))2]=n+n−1i=1∑n+j=1∑n−(1−wT(si+−sj−))2
s i + , s j − s_i^+, s_j^- si+,sj−分别表示正例和负例的得分。 这解释了为什么某些问题中,利用排序损失函数比logloss效果更好,因为在这些问题中排序比概率更重要!
AUC要到多少才算好的模型
AUC越大表示模型区分正例和负例的能力越强,那么AUC要达到多少才表示模型拟合的比较好呢?在实际建模中发现,预测点击的模型比预测下单的模型AUC要低很多,在月活用户里面预测下单和日常用户里面预测下单的AUC差异也很明显,预测用户未来1小时下单和预测未来1天下单的模型AUC差异也很大。这表明,AUC非常依赖于具体任务。
以预测点击和预测下单为例,下单通常决策成本比点击高很多,这使得点击行为比下单显得更加随意,也更加难以预测,所以导致点击率模型的AUC通常比下单率模型低很多。
那么月活用户和日活用户那个更容易区分下单与不下单用户呢?显然月活用户要容易一些,因为里面包含很多最近不活跃的用户,所以前者的AUC通常要高一些。
对于预测1小时和预测1天的模型,哪一个更加困难?因为时间越长,用户可能发生的意料之外的事情越多,也越难预测。举个极端的例子,预测用户下一秒中内会干啥,直接预测他会做正在干的事情即可,这个模型的准确率就会很高,但是预测长期会干啥就很困难了。所以对于这两个模型,后者更加困难,所以AUC也越低。