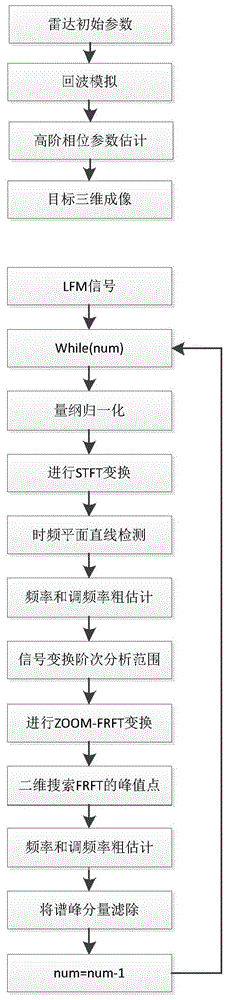
最近在做利用深度学习去噪的工作,大部分的工作都是利用spectrogram特征来做的,这就需要用到STFT, 本次利用的是python的scipy.signal模块。
在做去噪的时候,首先需要先将输入信号x利用stft转换成spectrogram:
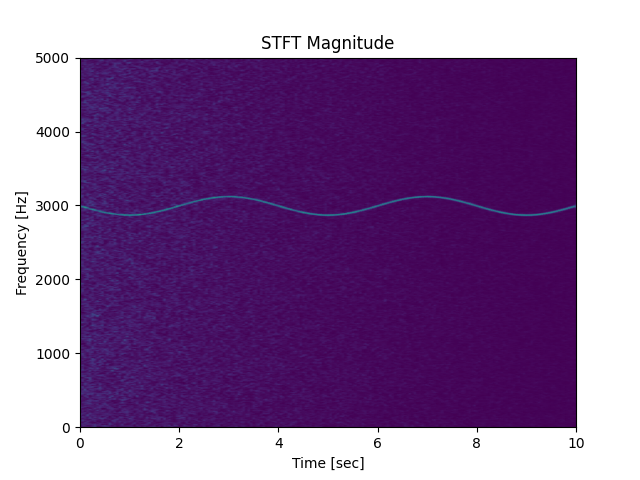
ff, tt, yyx = scipy.signal.stft(test_noise_, fs=48000, nperseg = N, noverlap = N//2)其中N表示的是fft的窗口长度(这里因为没有设置nfft,所以默认取nfft = nperseg), noverlap取的是N//2,表示有一半的信号重复计算。取N = 256 - 1, 那么得出来的yyx的shape就是128*128了,这样就能方便的使用一些基于图像的算法了。可以利用下面的代码来显示spectrogram (用imshow也可以,但是看得不是很明显,通过改cmap也许可行,但是不好找到跟下面图片一样的色彩配置):
plt.figure()
Pxx, freqs, bins, im = plt.specgram(test_noise_, NFFT=N, Fs=48000, noverlap=N//2)
plt.show()
在实际的操作中,往往取yyx的幅值,即np.abs(yyx),即将np.abs(yyx)来做为网络的输入(注意把信号归一化到-1~1之间要好得一些,图像它们的操作一般都会这么做),经过处理后会得到一些干净的spectrogram, 这个时候要还原成原始信号才能听得出差别来。而还原是要用到phase的,所以前面的步骤得把phase保存下来(注意在train的时候是不需要的, 在test的时候需要听出差别来,就要得到时域信号)。可以参与下面的操作来还完:
yyx_mag = np.abs(yyx) / np.max(np.abs(yyx)) * 2
yyx_phi = np.angle(yyx)xxx = np.multiply(yyx_mag, np.cos(yyx_phi)) + np.multiply(yyx_mag, np.sin(yyx_phi)) *1j这里得到的xxx就是还原的时域信号,可以用plt.spectrogram得到其频谱:

这里跟上面不完全一样是因为在转换的过程中存在精度损失。