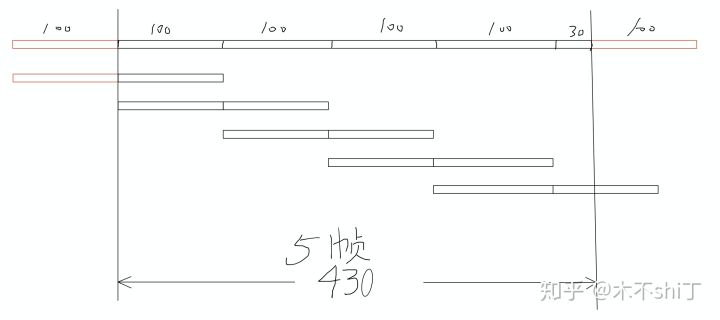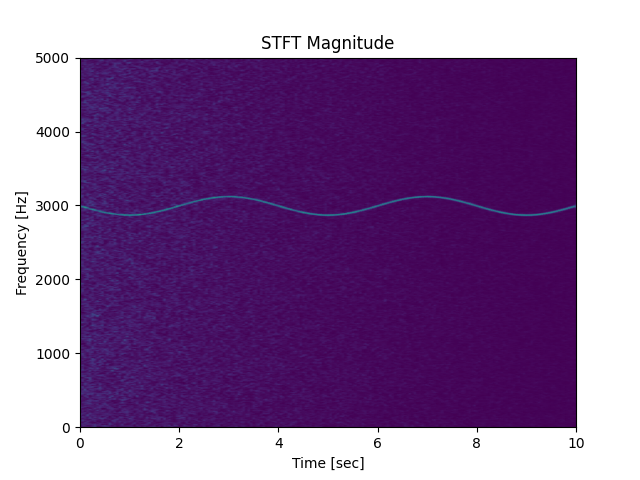
本发明属于数字信号处理技术领域，特别涉及一种运动目标雷达三维成像方方法，可 用于对运动目标识别时，雷达ISAR对其三维成像。

背景技术：

逆合成孔径雷达ISAR是一种全天候、全天时的远程探测手段，具有对运动目标进行 成像的能力，被广泛应用于目标跟踪、目标识别、机场监视等场合。相比于传统体制雷达， ISAR的高距离维分辨率源自其发射的宽带信号，而高方位维分辨率则依赖于雷达与目标 间相对运动产生的多普勒效应。

Ozaktas等人在“Ozaktas H M,et al.Digital computation of the fractional Fourier transform[J].IEEE Trans on SP,1996,44(9):2141-2150.”中提出分数阶傅里叶变换的 分解型算法，其利用傅里叶变换来计算分数阶傅里叶变换，计算复杂度为O(NlogN)。当 原始信号已经旋转到了合适的分数阶域之后，需要进行分数阶域的二维搜索，旋转角度越 小，二维搜索的计算量越大；若增加每次旋转的角度大小，会降低算法的计算量，但是同 时也会降低参数估计的精度。

贝苏章等人在“S C Pei,M H Yeh.Discrete fractional Fourier transform basedon orthogonal projections[J].IEEE Transactions on SP,1999,47(5):1335-1347.”中 提出通过求解离散傅里叶变换矩阵的Hermite特征向量构造离散分数阶傅里叶变换的核 矩阵，计算复杂度为O(N2)。传统分数阶傅里叶变换需要对原始信号从时频域旋转到分数 阶域，每次旋转的角度越小，划分的区间越精细，估计的精度越高，但是同时也会增加计 算的复杂度。

技术实现要素：

本发明的目的在于针对上述技术中存在的不足，提出一种基于短时傅里叶变换STFT 和精细化分数阶傅里叶变换FRFT的ISAR三维成像方法，以在有效地降低运算复杂度的同 时，提高参数估计的精度。

为实现上述目的，本发明的技术方案包括如下步骤：

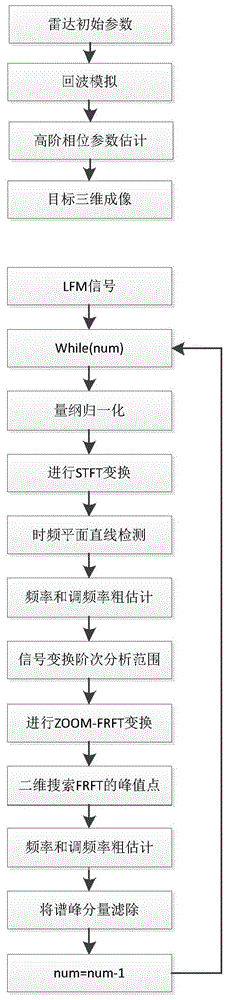
(1)模拟ISAR回波信号，得到原始回波信号s(t)；

(2)选择窗函数w(t)，对原始回波信号s(t)进行短时傅里叶变换，得到短时傅里叶变 换函数STFT(t,f)；

(3)在时频平面对短时傅里叶变换函数STFT(t,f)进行直线检测，通过在时频平面检测 到的直线࿰